Законы распространения света

Лучевая оптика заимствует от физической только основные положения. Такими положениями можно считать:
1. Прямолинейное распространение света в однородной среде.

2. Поведение света на границе раздела двух сред, когда эта граница представляет идеально гладкую поверхность»
3. Независимость распространения света.

Все эти положения, хотя и представляют лишь первое приближение к действительной физической картине, прочно установились и хорошо согласуются с опытом, за исключением особых, редко встречающихся в практике случаев, когда во избежание ошибок следует принимать во внимание действительную физическую картину явления.

Прямолинейность распространения света легко иллюстрируется явлением тени. Чтобы защитить глаза от жгучих лучей солнца, достаточно заслонить их рукой, как козырьком, чего не могло бы быть, если бы солнечные лучи огибали препятствия. Сидя в кинозале, мы можем наблюдать, как от проекционного окна к экрану тянутся пучки прямых лучей. Конечно, сами лучи, проходящие мимо глаз, невидимы, но, благодаря наличию в воздухе частичек пыли, которые, попадая в пучок, вспыхивают отраженным светом, их путь становится видимым.

Когда на пути луча оказывается какое либо прозрачное тело, например, стекло или вода, то, как показывает опыт, одна часть света входит в стекло, а другая отражается от поверхности раздела, то есть от той поверхности, которая отделяет пространство, занятое воздухом, от пространства, занятого стеклом.

При этом на поверхности раздела прямолинейность луча нарушается. Часть света, подчиняясь законам отражения, возвращается в ту же среду, а другая часть проходит границу раздела и продолжает распространяться так же прямолинейно внутри новой среды, изменив свое направление на границе раздела в соответствии с законами преломления.

Если, например, на плоскую, идеально гладкую поверхность раздела ММ (рис. 6) падает луч АБ, составляя, с нормалью ОБ к поверхности раздела угол АБО, то отраженный луч пойдет в направлении БВ, составляющем, с той же нормалью ОБ угол ОБВ, равный углу АБО, причем и падающий и отраженный лучи лежат в одной плоскости с нормалью.

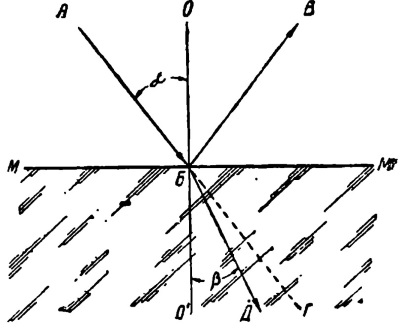
Рис. 6. Поведение луча на поверхности раздела

Этот закон формулируется обычно в виде следующих: двух положений:
1. Угол падения равен углу отражения.
2. Луч падающий и луч отраженный лежат в одной плоскости с нормалью в точке падения.

Другая часть света, пройдя поверхность раздела, также изменит свое направление и будет продолжать путь по новому направлению БД, составляющему с продолжением нормали БО' угол преломления О'БД, меньший угла падения АБО.

Это отклонение луча от прямой, происходящее на поверхности раздела, называется преломлением света, а сама поверхность— преломляющей поверхностью.

Преломление происходит во всех случаях, когда свет переходит из одной среды в другую, обладающую другими физическими свойствами. Величина отклонения луча от прямой, то есть степень преломления при прочих равных условиях, зависит от того, насколько отличаются эти две- среды между собой.

Законы преломления сложнее, чем законы отражения, и для случая перехода луча из пустоты в прозрачное вещество формулируются следующим образом:

1. Луч падающий и луч преломленный лежат в одной плоскости с нормалью к поверхности раздела в точке падения луча.
2. Отношение синуса угла падения к синусу угла преломления остается неизменным при любом значении угла падения, то есть

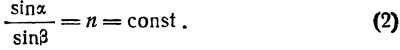
Это отношение называется абсолютным показателем преломления того вещества, в которое входит луч из пустоты, или даже просто показателем преломления.

Показатель преломления для всех прозрачных тел больше, чем единица, и для подавляющего большинства прозрачных тел меньше двух. Лишь в отдельных случаях показатель преломления превосходит значение „2“. Чем больше показатель преломления n, тем оптически более плотным считается вещество. Для пустоты n равняется единице.

В табл. 1 приведены значения показателя преломления для некоторых прозрачных тел.

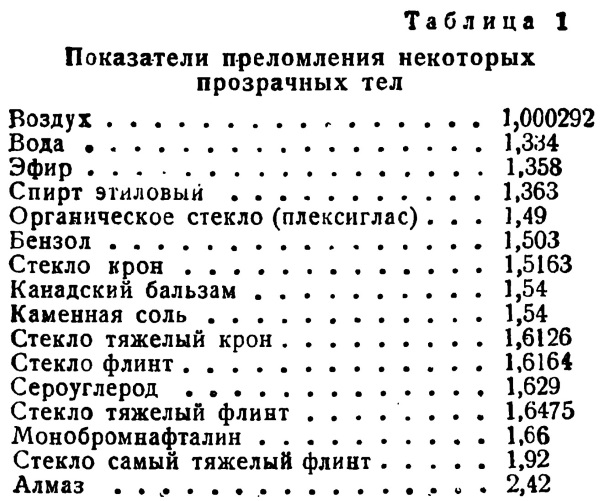
Если луч переходит из одного прозрачного тела, например, из воды в другое прозрачное тело, например, в стекло, то показатель преломления называется относительным и составляет:

где n₁ и n₂—абсолютные показатели преломления для> первой и второй среды относительно пустоты.

Так как показатель преломления воздуха мало отличается от единицы, то показатель преломления вещества обычно определяют не относительно пустоты, а относительно воздуха.

В прозрачной среде скорость распространения света в n раз меньше, чем в пустоте. Здесь n —показатель преломления. Кроме того, эта скорость различна для различных длин волн, тогда как в пустоте скорость распространения любого вида лучистой энергии одинакова для любой: длины волны. Среда как бы оказывает некоторое сопротивление прохождению света, и это сопротивление тем больше, чем больше оптическая плотность среды и чем выше частота колебания, то есть чем короче длина волны света.

Таким образом, показатель преломления n прозрачного» вещества служит мерой его оптической плотности. Поэтому, определяя показатель преломления, следует указать,, к какой длине волны относится данный показатель. Это указание делается припиской к букве п длины волны или другой буквы, условно обозначающей эту длину. Например: n₅₈₉ или n_D означает показатель преломления для длины волны 589 mμ.

Из формул (2) и (3) следует, что нахождение направления преломленного луча сложно и сопряжено с поисками» значения синусов заданных углов и в дальнейшем по значениям синусов отыскивания значения самих углов. Это действительно имеет место при расчетах оптических Систем, представляющих довольно кропотливый труд, но существуют очень простые и наглядные графические методы, построения преломленных лучей, позволяющие легко определять направление преломления.

Пусть задан луч АБ (рис. 7), падающий из воздуха на поверхность стекла ММ, показатель преломления которого составляет:

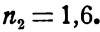
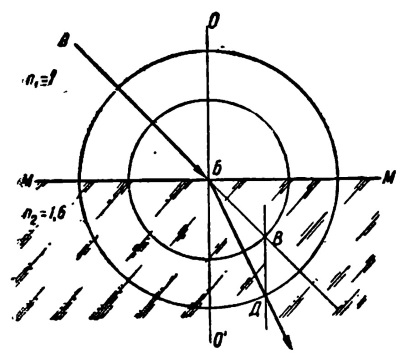
Рис. 7. Построение преломленного луча

Из точки Б, как из центра, описываем в любом масштабе- две окружности: одну—радиусом, равным единице (на рисунке взято 10 мм) и другую радиусом 1,6 (следовательно 10 X 1,6 = 16мм). Продолжаем прямую АБ до пересечения с малой окружностью в точке В. Через точку В проводим прямую, параллельную нормали 00', и соединяем точку Б с точкой Д пересечения этой прямой с большой окружностью.

Прямая БД будет точным направлением преломленного луча. Таким же образом может быть решена обратная задача, когда дан угол преломления и требуется на основании показателя переломлення определить угол падения или когда даны оба угла и требуется определить показатель преломления.

Прибегать постоянно к таким точным построениям нет никакой необходимости и обычно ограничиваются проведением линий, показывающих направление лучей от руки, но когда нет уверенности, в каком направлении пойдет луч после преломления, указанный способ применяется как вполне разрешающий все сомнения.

Основным моментом построения является проведение нормали к рассматриваемой поверхности раздела в точке падения луча. Когда проведена нормаль и определился угол падения луча, то есть угол между падающим лучом и нормалью, построение отраженного или преломленного луча уже не представляет никакого труда.

В случае не плоской, а, например, шаровой поверхности раздела, которую имеют стекла наших объективов, — нормалью, как известно, будет являться радиус кривизны, проведенный из центра кривизны к точке падения луча. Сама кривая линия может быть заменена касательной к кривой в этой точке, и весь ход рассуждения остается тем же.

На рис. 8 дано построение преломленного луча, когда «а шаровую поверхность раздела падает луч АБ.

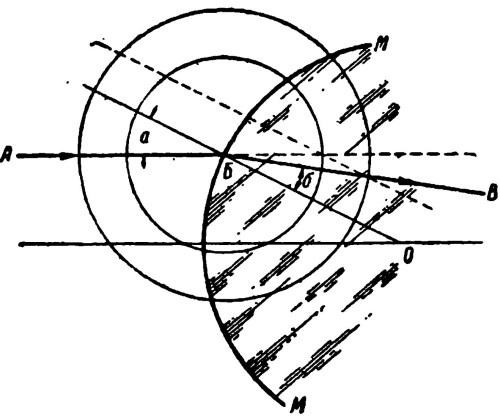
Рис. 8. Преломление на сферической поверхности

Если луч падает на поверхность раздела по нормали, то есть перпендикулярно к поверхности раздела, то угол падения будет равен нулю и, следовательно, угол отражения и угол преломления также будут равны нулю, то есть луч, падающий на поверхность раздела по нормали, не будет испытывать отклонения. Отраженный луч возвратится обратно, совпадая с падающим лучом, а преломленный придет в новую среду без отклонения.

До сих пор мы рассматривали переход луча из пустоты в прозрачное тело. Теперь разберем обратный случай, когда луч подходит к поверхности раздела со стороны более плотной среды, например из стекла, с показателем преломления n₁ = 1,5, входит в пустоту или в воздух с показателем преломления n₂ = 1,0.

Допустим, на рис. 9 ММ— поверхность раздела, и из точки А, находящейся в стекле, выходит пучок лучей АО, АБ, AB и т. д. В этом случае угол преломления будет больше угла падения, то есть преломленный луч. будет удаляться от нормали. Если угол падения будет постепенно возрастать, преломленный луч будет все больше приближаться к поверхности раздела, наконец, он будет скользить по этой поверхности, как луч АГМ, и при дальнейшем возрастании угла падения луч уже не будет преломляться, а отразится от ММ и вернется обратно, подчиняясь законам отражения.

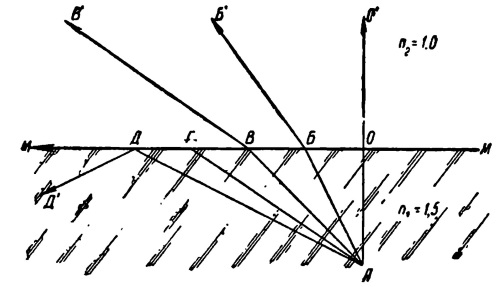
Рис. 9. Полное внутреннее отражение

Такое отражение называется полным внутренним отражением, а наибольшее значение угла падения, при котором еще происходит преломление, называется предельным, или критическим, углом преломления.

Значение предельного угла легко определить из формулы (3), если предположить, что угол преломления ß равен 90°, а показатель преломления воздуха n₂ = 1.

Тогда имеем:

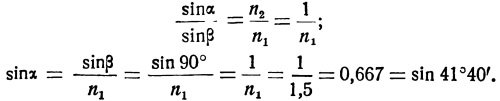
Таким образом, при n₁ = 1,5 все лучи, падающие на поверхность раздела под углом больше, чем 41° 40', уже не будут преломляться, а отразятся обратно в стекло. Если взять стекло с большим показателем, например, n = 1,7, то критический угол будет еще меньше:

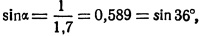
то-есть в этом стекле будут отражаться все лучи, падающие под углом больше 36°.

Полное внутреннее отражение находит широкое применение в отражательных призмах. Поведение луча на границе раздела представляет собой основу прикладной оптики — тот фундамент, на котором построены все расчеты оптических приборов. Оптические приборы представляют собой сочетание поверхностей раздела, расположенных по ходу пучка света, а любой расчет оптической системы состоит из последовательного приложения законов отражения и преломления ко всем по ходу света поверхностям раздела, содержащимся в оптическом приборе.

Гораздо меньшую роль играет третий закон — закон независимости распространения света. Согласно этому закону отдельные пучки света, входящие в сложный поток, распространяются независимо друг от друга, то-есть каждый пучок распространяется так, как если бы не было других пучков. Например, два или три пучка света могут пересекаться между собой, не заслоняя и не перебивая друг друга и вообще не производя один на другой какого-либо воздействия, а если два или несколько пучков падают на одну общую поверхность, их действия складываются, так как каждый из них действует независимо от других.

Таким образом, закон независимости распространения света не принимает непосредственно участия в каких-либо расчетах и не фигурирует в формулах. Он только дает основание обращаться с каждым пучком независимо от его положения в общем потоке относительно других пучков.

Чтобы усвоить принцип построения луча при прохождении его через прозрачные тела, рассмотрим два простейших типовых примера.

Пусть пучок параллельных лучей падает на ступенчатую стеклянную пластинку (рис. 10), окруженную воздухом. Выберем из пучка два луча АБ и ДЕ и проследим их путь через пластинку.

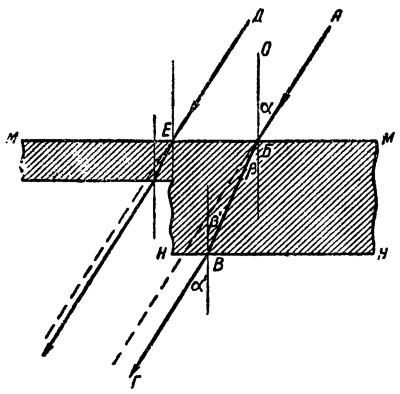
Рис. 10. Смещение луча при прохождении через плоскопараллельную пластинку

Луч АБ, упавший на плоскость ММ под углом α к нормали ОБ, пойдет внутри стекла под углом ß, причем ß будет меньше, чем α. Подходя к плоскости НН, луч образует с нормалью, ввиду параллельности ММ и НН, угол ß', равный углу ß, но в таком случае и угол α' будет равен углу α, так как углы α и ß связаны отношением:

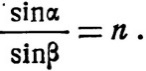
Следовательно, пройдя плоскопараллельную пластинку, луч будет продолжать путь параллельно первоначальному направлению, не отклонившись, а только получив некоторое смещение.

Из рис. 10 видно, что это смещение будет тем больше, чем больше толщина пластинки и показатель преломления n.

При очень малой толщине смещение будет настолько незначительным, что луч света можно считать проходящим без отклонения и без смещения.

Возьмем вместо плоскопараллельной пластинки призму, то-есть кусок стекла, ограниченный двумя непараллельными плоскостями КЛ и ЛМ (рис. 11). Луч света АБ, пройдя через грань НЛ, приблизится к нормали ОО’, то-есть отклонится к основанию призмы KМ. Выходя из призмы через грань ЛМ, он удалится от нормали НН', то-есть, как видно из рисунка, еще раз отклонится опять к основанию призмы и пойдет окончательно по линии ВГ, составляющей с первоначальным направлением АЕ некоторый угол б, зависящий от величины угла КЛМ, называемого преломляющим углом, и от показателя преломления вещества призмы.

Чем больше величина преломляющего угла и чем больше показатель преломления, тем больше отклоняется луч при прохождении через призму. При уменьшении преломляющего угла уменьшается и отклонение, и когда угол между гранями призмы будет равен нулю, то-есть когда призма превратится в плоскопараллельную пластинку, то и отклонение будет равно нулю.