Крыло самолета. Геометрическая характеристика крыла

Нам известно, что сопротивление воздуха сильно зависит от формы тела. Это справедливо, разумеется, и для крыла. Придавая крылу ту или иную форму, мы тем самым будем несколько изменять обтекание крыла, а следовательно будем изменять и его аэродинамические свойства. Подъемная сила и лобовое сопротивление и их соотношение (качество крыла) зависят, как мы видели, от угла атаки; у разных же по форме крыльев зависят еще и от формы крыла.

При одном и том же угле атаки у крыльев разной формы и качество может быть разным, а качество является основным критерием для аэродинамической оценки крыла. Таким образом, аэродинамические свойства крыла сильно зависят от его геометрической формы.

Геометрическая форма крыла — это форма его в плане (вид крыла сверху) и в поперечном сечении (форма профиля).

Форма крыла в плане может быть разнообразной (рис. 107). Прямоугольная форма (рис. 107, I) — наиболее простая и легко выполнимая в конструктивном отношении (при свободнонесущем крыле невыгодна в отношении прочности). Трапецевидная форма (рис. 107, II) наиболее распространена. Эллиптическая форма (рис. 107, III) — саман выгодная в аэродинамическом отношении, но трудно выполнимая в конструктивном. Параболическая форма (рис. 107, IV) встречается редко.

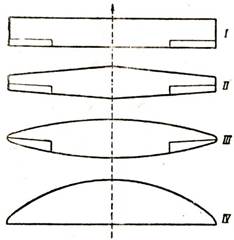
Рис. 107. Формы самолетного крыла в плане

Концы крыльев обычно закругляются, так как это аэродинамически выгодно (причина будет объяснена позже).

На рис. 108 изображен вид самолетного крыла в плане: AB — передняя кромка крыла, С задняя кромка, АBСD - площадь крыла S, l — размах крыла, b - глубина крыла.

Рис 108. Площадь, размах и глубина крыла

Площадь прямоугольного крыла равна, очевидно, произведению размаха на глубину: S = lb.

В случае трапецевидного крыла, у которого глубина различна по размаху (рис. 109), для вычисления площади крыла берется средняя глубина (b_ср). Следовательно, площадь крыла в этом случае: S = lb_ср.

Рис. 109. Площадь трапецевидного крыла

Отношение размаха к глубине называется удлинением крыла (обозначается греческой буквой λ — „лямбда“). Таким образом, удлинение крыла λ = l/b.

В некоторых случаях удлинение выражают через площадь крыла. Из формулы для площади нетрудно получить, что глубина крыла b = S/l. Подставив это выражение в формулу удлинения, получим: λ = l²/S.

Удлинение крыла имеет очень большое значение: чем больше удлинение, тем выгоднее крыло в аэродинамическом отношении (о причине этого будет рассказано позже). У самолетов удлинение крыла бывает от 6 до 12, у планеров доходит до 20.

Аэродинамические свойства крыла особенно сильно зависят от формы крыла в поперечном сечении, т. е. от формы профиля.

Формы профилей чрезвычайно разнообразны (исследованы тысячи различных профилей). Однако все они могут быть разделены на четыре типичные группы (рис. 110): профили с вогнутым основанием (I), с плоским основанием (II), двояковыпуклые (III) и симметричные (IV). У каждого из этих профилей показана линия ab; эта линия называется, как мы уже знаем, хордой профиля (хордой крыла).

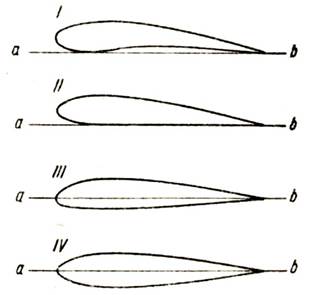
Рис. 110. Основные формы профилей крыльев

У профилей с вогнутым и плоским основанием хордой, следовательно, называется прямая линия, касательная к нижнему обводу профиля; у двояковыпуклых и симметричных профилей хордой называется прямая, проведенная через переднюю и заднюю кромки профиля.

Заметим, что на практике за длину хорды принимают отрезок линии b (рис. 111), ограниченный двумя перпендикулярами, касательными к передней и задней кромкам профиля. Можно, следовательно, сказать что хорда профиля равна глубине крыла. Следует иметь в виду, что у всякого крыла, кроме прямоугольного, длина хорды меняется по размаху, как это нетрудно видеть из рис. 107.

Рис. 111. Профиль крыла, его хорда и относительная толщина (h/b)

На рис. 111 дан профиль крыла: b - хорда профиля; h — высота профиля. Отношение высоты к длине хорды (к глубине), т. е. h/b, называется относительной толщиной профиля.

В зависимости от толщины профиля крылья разделяются на тонкие, средние и толстые (рис. 112). Если относительная толщина профиля (отношение h/b) меньше 8% от длины хорды, то такой профиль называют тонким. Профили, у которых толщина равна 8—12% длины хорды, считаются средними. Если же относительная толщина профиля больше 12% длины хорды, то такой профиль считают толстым.

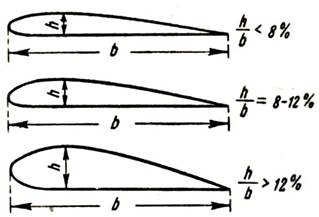
Рис. 112. Тонкий, средний и толстый профили

Об аэродинамических свойствах различных профилей мы пока говорить не будем. Заметим лишь, что в зависимости от требований, которые предъявляются тому или иному типу самолета, т. е. в зависимости от заданных скорости, грузоподъемности и других летных качеств, выбирается тот профиль, который в данном случае даст наибольший аэродинамический эффект. Для нахождения наиболее выгодных профилей крыльев производят сложные теоретические исследования, но в основу их кладется всегда опыт, т е. испытание различных профилей в аэродинамической трубе.