Давление движущегося воздуха. Закон Бернулли

Опыт и теория показывают, что давление движущегося воздуха находится в определенной зависимости от скорости частиц воздуха (в струе, в потоке). Движение газов и жидкостей подчиняется в основном одним и тем же законам, поэтому указанную зависимость мы выясним сначала на примере движения воды.

На рис. 55 изображена схема прибора, представляющего собой трубу переменного сечения. Если открыть краны и поддерживать уровень воды в резервуаре постоянным, то из трубы в 1 секунду через кран будет вытекать такой же объем воды, какой будет притекать за 1 секунду в трубу из резервуара.

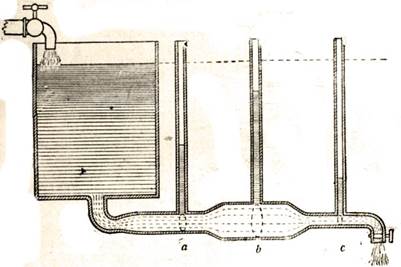
Рис. 55. Схема прибора для опытного доказательства закона Бернулли

Отсюда следует, что и через сечения а, b, с будет протекать в 1 секунду такой же объем воды, несмотря на то, что эти сечения неравные. Но если через неравные сечения протекает в единицу времени одинаковый объем воды, то, очевидно, через эти сечения вода течет с разными скоростями. И, очевидно, чем меньше сечение, тем больше скорость частиц воды (иначе через узкое сечение не мог бы пройти в секунду объем воды, который проходит в секунду через широкое сечение).

В справедливости этого мы можем убедиться, наблюдая, например, течение реки: там, где русло ее уже и мельче, течение всегда быстрее. Подобно этому же ветер, врываясь в ущелье, дует здесь сильнее, чем на открытом месте.

В нашей трубе мы имеем так называемое установившееся течение воды. Так называются течения, при которых в каждой точке струн (потока) скорость не меняется во времени, хотя в разных точках она может быть различной. При установившемся течении траектории частиц жидкости (газа) называют линиями тока.

Линии тока можно сделать видимыми, если чем-нибудь загрязнить текущую жидкость (газ): воду, например, алюминиевым порошком, воздух — дымом. Если нанести линии тока на чертеж (рис. 56), то они дадут нам представление не только о направлении движения частиц, но и о их скорости.

В самом деле, в узком сечении струи, где скорость, как мы выяснили, увеличивается, линии тока сближаются друг с другом —становятся гуще. Таким образом, по густоте линий тока мы можем судить о скорости частиц в струе или потоке (на рис. 55 линии тока показаны пунктирными линиями, в дальнейшем же мы всегда будем изображать их сплошными тонкими линиями, как это сделано на рис. 56).

Рис. 56. Графическое изображение линий тока

Итак, чем меньше сечение струи, тем больше скорость частиц жидкости (газа). Помня это, вернемся к опыту с движением воды по трубе переменного сечения (рис. 55).

Как видим, труба имеет отростки — трубки с открытыми концами; эти трубки будут играть роль манометров. Если бы краны были закрыты, т. е. если бы вода не текла по трубе, а находилась в покое, то вода в трубках стояла бы, конечно, на том же уровне, что и в резервуаре (сообщающиеся сосуды).

При нашем же опыте мы заметим, что лишь только вода потечет по трубе, как уровень воды в манометрах понизится, причем больше всего в том манометре, который присоединен к самому узкому сечению трубы, и меньше всего в том, который присоединен к наиболее широкому сечению. Отсюда мы можем сделать весьма важный для нас вывод, что при сужении струи, т. е. при увеличении скорости частиц воды, давление в струе уменьшается.

То же самое явление мы будем наблюдать и при движении газа по трубе переменного сечения (рис. 57). Микроманометры и здесь покажут нам, что давление будет уменьшаться при сужении струи, т. е при увеличении скорости частиц газа.

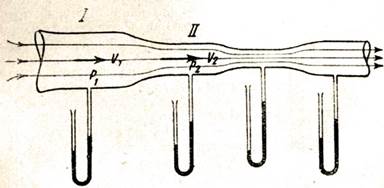
Рис. 57. При увеличении скорости струи газа давление в струе уменьшается (к закону Бернулли)

Таким образом, мы установили, что при увеличении скорости движения газа давление в струе уменьшается.

Какая же причина этого явления? Движущийся сжатый газ может производить работу, т. е. обладает некоторым запасом энергии, состоящим из потенциальной энергии газа (энергий давления) и кинетической энергии (энергии движения).

Когда газ движется по трубе, он не производит работы, и поэтому общий запас его энергии — потенциальной и кинетической — остается неизменным (если не считать некоторых потерь на преодоление трения газа о стенки). Но, как мы знаем из механики, всегда возможен переход части потенциальной энергии в кинетическую, и наоборот. Это и имеет место при движении газа (и жидкости) по трубе переменного сечения.

Когда скорость газа увеличивается, то увеличивается и его кинетическая энергия; но так как общий запас его кинетической и потенциальной энергии должен остаться неизменным, то ясно, что увеличение кинетической энергии газа может произойти лишь за счет уменьшения его потенциальной энергии (энергии давления). Отсюда и понятно, почему при увеличении скорости струи (что имеет место при ее сужении) давление в струе становится меньше.

Наоборот, при уменьшении скорости кинетическая энергия уменьшается, а это неизбежно ведет к увеличению потенциальной энергии газа; поэтому при уменьшении скорости струи (что имеет место при ее расширении) давление в струе увеличивается.

Потенциальная энергия движущегося газа называется статическим давлением, или просто давлением. Статическое давление движущегося газа — это давление газа на поверхность (стенку), вдоль которой газ движется, т. е. параллельную линиям тока (поэтому мы и смогли обнаружить это давление манометрами, включенными в стенку трубы).

Статическое давление движущегося газа подобно давлению покоящегося газа (в обоих случаях — это потенциальная энергия); измеряется оно в миллиметрах ртутного (или водяного) столба и в кг/м² (обозначается буквой р).

Кинетическая энергия движущегося газа проявляет себя динамическим давлением или, как говорят, скоростным напором. Скоростной напор — это давление струи газа на поверхность, перпендикулярную линиям тока. В этом легко убедиться на простом опыте с изогнутой трубкой, наполненной водой (рис. 58); если дуть по оси трубки (слева направо), то под действием скоростного напора уровень воды в левом колене понизится (струя воздуха гонит воду вниз).

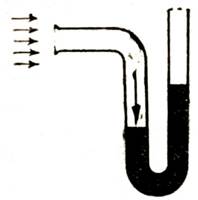
Рис. 58. Динамическое давление, или скоростной напор струи газа

Так как скоростной напор есть кинетическая энергия газа, то для определения величины скоростного напора мы можем воспользоваться известной нам из механики формулой кинетической энергии твердого тела (K = mv²/2), заменив в ней массу тела m массовой плотностью газа р. Следовательно, для скоростного напора (обозначается буквой q) получим следующую формулу: q = pV²/2.

(Заметим, что воздушную скорость в аэродинамике принято обозначать через V, так мы и будем делать в дальнейшем.) Скоростной напор, как и статическое давление, выражается в кг/м². Чтобы убедиться в этом, перемножим размерности величин, входящих в правую часть формулы:

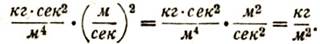
Выше мы выяснили, что общий запас энергии движущегося газа (потенциальной плюс кинетической) остается неизменным во всех сечениях трубы (рис. 57). Иными словами, это означает, что сумма статического давления и скоростного напора в каком-нибудь сечении трубы равна сумме статического давления и скоростного напора в любом другом сечении, т. е. для всех сечений труби эта сумма есть величина постоянная (const.).

Запишем это математически. Обозначим в каком-нибудь сечении I трубы статическое давление через p₁, и скорость через V₁, а в каком-нибудь сечении II — давление через р₂ и скорость через V₂. Получим:

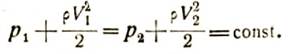
Это уравнение выражает собой закон распределения давления в струе жидкости, открытый в середине XVIII в. голландским ученым Даниилом Бернулли.

Закон (теорема) Бернулли в полной мере справедлив лишь для так называемой идеальной жидкости (идеального газа). Под этим названием подразумевают воображаемую жидкость (газ), которая не обладает вязкостью. Дело в том, что молекулы жидкости (газа) находятся в постоянном движении и, сталкиваясь, оказывают друг другу сопротивление; при этом развиваются силы, называемые силами внутреннего трения.

Эти силы внутреннего трения и есть вязкость. Существующие (реальные) жидкости и газы всегда обладают в той или иной мере вязкостью(вязкость обратно пропорциональна плотности). Поэтому при движении реальной жидкости (газа) некоторая часть энергии тратится на преодоление сил внутреннего трения, и, следовательно, общий запас энергии, строго говоря, не остается постоянным.

Воздух и вода близки к идеальным жидкостям, и трата энергии на преодоление сил внутреннего трения в них незначительна; поэтому для практических целей этими потерями пренебрегают (при больших скоростях вносят поправку на вязкость).

Итак, уравнение Бернулли говорит нам, что сумма статического давления и скоростного напора есть величина постоянная для всех сечений струи. Эта сумма p + pV²/2 называется полным давлением или, иначе, полным напором.

Из уравнения Бернулли следует:

1) что разность давлений равна разности скоростных напоров:

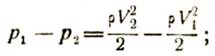
2) что увеличение скоростного напора вызывает уменьшение давления.

Второй вывод особенно для нас важен; его можно запомнить в данной раньше формулировке: при увеличении скорости струи давление в ней уменьшается.