Равномерное движение по окружности

Простейшим криволинейным движением является равномерное движение по окружности.

Пусть материальная точка движется равномерно по окружности радиуса r (рис. 34) и за Т секунд описывает полную окружность 2πr. Нетрудно понять, что если разделить всю длину окружности 2πr на время Т, то мы получим скорость V, с которой точка движется по окружности: v = 2πr/T.

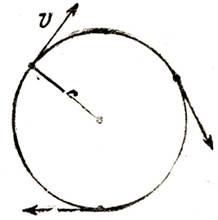
Рис. 34. Движение материальной точки по окружности (скорость всегда направлена по касательной к окружности)

Скорость V называется окружной скоростью точки. Окружная скорость — это длина дуги, которую точка проходит в 1 секунду.

Заметим, что окружная скорость всегда направлена по касательной к окружности (рис. 34).

Время Т, в течение которого точка описывает полную окружность, называется периодом обращения.

Радиус r называется радиусом-вектором.

На практике вместо периода Т часто дается число оборотов n, которое точка делает в 1 секунду (или минуту).

Нетрудно сообразить, что если n число оборотов в 1 секунду, то один полный оборот точка совершит в течение 1/n сек. Следовательно, период обращения T = 1/n, откуда n = 1/T.

Таким образом, по числу оборотов в секунду мы всегда можем узнать период обращения, и обратно, по периоду обращения всегда можем узнать число оборотов в секунду.

Подставив в формулу окружной скорости вместо Т выражение 1/n , получим: v = 2πrn.

Эта формула показывает, что окружная скорость точки будет тем больше, чем больше радиус вращения и чем больше число оборотов в секунду.

В самом деле, пусть мы имеем равномерно вращающийся воздушный винт самолета (рис. 35). Очевидно, что точки, лежащие на разных расстояниях от центра вращения, будут иметь и разные окружные скорости; например, точка В, лежащая вблизи втулки, будет описывать за одно и то же время меньшую окружность, чем точка А, лежащая у конца лопасти. Понятно также, что при увеличении числа оборотов винта окружные скорости взятых нами точек возрастут, а при уменьшении числа оборотов станут меньше.

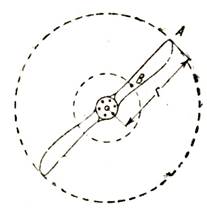
Рис. 35. Точки А и В винта вращаются с одинаковой угловой скоростью, но окружные их скорости различны

При движении по окружности, кроме окружной скорости, приходится иметь дело еще с так называемой угловой скоростью, которая не зависит от радиуса вращения, а только от периода обращения или числа оборотов. Если, например, мы имеем равномерно вращающийся воздушный винт, то все точки его, независимо от их радиусов вращения, будут за 1 секунду описывать один и тот же угол, причем этот угол будет меняться лишь в том случае, если будет меняться число оборотов винта в секунду.

Углы при вращательном движении выражаются не в градусах, а в угловых единицах, или радианах. Радианом называется угол, длина дуги которого равна радиусу. Так как по всей окружности укладывается 2π радиусов и она содержит 360°, то дуга длиною в один радиус содержит 360^о/2π, т. е. один радиан равен 57° 17'45’’.

Угловой скоростью называется угол, выраженный в радианах, на который повернется радиус-вектор в 1 секунду. Так как по всей окружности укладывается 2π радиусов, а время, за которое радиус-вектор описывает всю окружность, равно Т секунд (период обращения или время одного оборота), то угловая скорость, обозначаемая греческой буквой ω (омега), напишется так: ω = 2π/T.

Найденную выше формулу окружной скорости v = 2πr/T мы можем написать так: v = 2π/T ∙ r.

Но 2π/T есть угловая скорость ω. Таким образом, мы нашли, что окружная скорость v = ωr, т. е. окружная скорость равна угловой скорости, помноженной на радиус вращения.