Что такое криволинейное движение?

Пусть самолет летит прямолинейно и горизонтально с некоторой постоянной скоростью и с него сброшена бомба (рис. 31). Отделившись от самолета, бомба будет продолжать по инерции двигаться горизонтально (с прежней скоростью), и если бы на нее не действовала сила земного притяжения, то в конце первой секунды она оказалась бы в точке А₁, в конце второй — в точке А₂ в конце третьей — в точке А₃ и т. д.

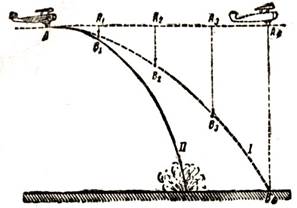
Рис. 31. Траектория падения бомбы: I - без учета сопротивления воздуха; II — действительная траектория

Под действием силы земного притяжения бомба, двигаясь по инерции горизонтально, одновременно будет и падать с ускорением g = 9,8 м/сек. Оба эти движения бомбы, иначе говоря, обе ее скорости (горизонтальная и вертикальная), будут складываться по правилу сложения скоростей, направленных под углом друг к другу, в результате чего бомба в конце первой секунды окажется в точке В₁, в конце второй — в точке В₂, в конце третьей — в точке В₃, и т. д.

Соединив точки В₁, В₂, В₃..., плавной линией, мы получим траекторию движения бомбы. Эта кривая линия носит название параболы.

Но в наших рассуждениях мы не принимали в расчет сопротивления воздуха. Вследствие сопротивления воздуха горизонтальная скорость бомбы не будет постоянной, а будет равномерно уменьшаться, т. е. горизонтально бомба будет двигаться равномерно-замедленно; сопротивление воздуха скажется и на падении бомбы: она будет падать не с одним и тем же ускорением (как тела падают в пустоте), а неравномерно-замедленно (ускорение будет уменьшаться). Таким образом, в действительности траектория бомбы будет примерно такая, какая показана на рис. 31 жирной линией.

Если, подобно движению бомбы, мы рассмотрим движение камня, брошенного под углом вверх, или снаряда, выпущенного из орудия (рис. 32), то убедимся, что движение камня или снаряда будет иметь траекторию (тоже параболу), изображенную на нашем рисунке.

Рис. 32. Траектория снаряда, выпущенного из орудия

Итак, криволинейное движение получается в результате сложения двух неравномерных прямолинейных движений.

Скорость при криволинейном движении в любой момент равна векторной сумме скоростей составляющих движений и направлена по касательной к траектории в той точке, в которой находится движущееся тело в этот момент. В последнем нетрудно убедиться. Пусть MN есть путь s, который проходит материальная точка А за время t по своей кривой траектории (рис. 33).

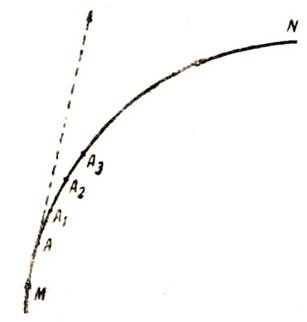
Рис. 33. Направление скорости при криволинейном движении

Если мы время движения t разобьем на весьма большое число n весьма малых промежутков времени и обозначим один такой промежуток времени через Δ (греческая буква „дельта“), то Δt = t/n. За каждый такой бесконечно малый промежуток времени точка А будет перемещаться по кривой на столь ничтожный отрезок МА, что такой отрезок без существенной погрешности можно принять за прямолинейный.

Таким образом, движение по кривой мы можем рассматривать как ряд последовательных прямолинейных движений МА, АА₁, А₁ А₂, каждое из которых длится ничтожно малый промежуток времени Δt. Так как направление кривой в точке А определяется касательной к этой точке, то из этого следует, что и направление скорости будет определяться тоже касательной к этой точке.

Итак, скорость при криволинейном движении всегда направлена по касательной к кривой.