Потенциальная и кинетическая энергия (живая сила)

Тело, поднятое на некоторую высоту, может произвести работу, если ему будет предоставлена возможность падать с высоты; свернутая пружина может произвести работу, если ей будет дана возможность раскручиваться; сжатый газ может произвести работу, если ему будет дана возможность расширяться, и т. д.

В подобных случаях, когда тело остается в покое, его энергия находится как бы в скрытом виде и ничем себя не проявляет. Такой вид энергии называется энергией положения, или потенциальной энергией.

С другой стороны, работу может произвести всякое движущееся тело: брошенный камень, летящий снаряд, вращающийся вал двигателя, движущийся паровоз и т. д.

Следовательно, все эти тела обладают энергией. Энергия, которой обладает движущееся тело, называется энергией движения, или кинетической энергией.

Определим потенциальную энергию тела, поднятого на некоторую высоту.

Пусть некоторой груз весом в G кг поднят на высоту, например „баба“, применяемая для закалачивания свай (рис. 30). Очевидно, что в таком положении груз обладает некоторым запасом потенциальной энергии и может произвести некоторую работу, если ему дать возможность падать. Обозначим потенциальную энергию груза на высоте h через Е, а работу, которую груз может выполнить, падая до земли, через А.

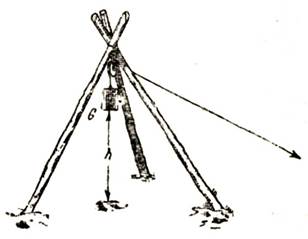
Рис. 30. Потенциальная энергия груза, поднятого на высоту

Так как работа равна силе, помноженной на проходимый телом путь, то A = Gh.

Упав до земли, груз истратит всю свою потенциальную энергию. Так как убыль энергии равна совершенной телом работе, то Е=А; следовательно E = Gh.

Таким образом, потенциальная энергия поднятого груза равна произведению веса груза на высоту, на которую он поднят.

Потенциальная энергия скрученной пружины, сжатого газа (и в других случаях) может быть также без труда определена, но мы не будем на этом останавливаться.

Найдем теперь формулу для определения кинетической энергии тела.

Пусть машинист паровоза закрыл пар и паровоз движется прямолинейно и равномерно-замедленно (по инерции). Обозначим массу паровоза через m и скорость его в некоторый момент через v.

Найдем, чему будет равна кинетическая энергия паровоза в этот момент. Очевидно, что с того момента, когда машинист закрыл пар, и до того момента, когда скорость паровоза, уменьшаясь, стала равной v, кинетическая энергия паровоза уменьшилась на величину проделанной паровозом работы, заключавшейся в преодолении силы сопротивления (силы трения и силы сопротивления воздуха).

Если обозначить силу сопротивления через f, а путь, пройденный паровозом с момента закрытия пара до того момента, когда его скорость стала равной v, через s, то мы можем написать, что проделанная паровозом работа A = fs (так как работа равна силе, помноженной на пройденный телом путь).

Но выполненная паровозом работа равна убыли его кинетической энергии. Обозначим ее через К, т. е. А = К следовательно: K = fs.

Выразим кинетическую энергию паровоза через его массу m и скорость v. Для этого вспомним, что сила f=ma, а путь s = v²/2α. Подставим эти значения для f и s в нашу формулу.

Тогда получим: K = fs = mα ∙ v²/2α, или после сокращения на α: K = mv²/2

Таким образом, мы нашли, что кинетическая энергия тела равняется половине произведения массы тела на квадрат скорости.

Выражение mv²/2 часто называют живой силой тела. Поэтому можно сказать, что кинетическая энергия тела равна его живой силе.

Кинетическая энергия, как и потенциальная, выражается в килограммометрах (кгм); нужно только при ее определении массу тела выражать в технических единицах массы (кг∙сек²/м), а скорость - в метрах в секундах (м/сек).