Динамический анализ. Продвижение разломов в сложных системах

Динамический анализ. Для изотропных пород известна общая связь между сдвиговыми смещениями по разлому и главными осями напряжений, вытекающая из экспериментальных (рис. 3.1) и полевых наблюдений и хорошо описываемая с помощью диаграммы Мора (разд. 2.3.2 и 3.2.2).

На рис. 5.12 показана эта связь для различных типов разломов. По данным для двух сопряженных разломов можно найти направления главных осей напряжений. Главная ось напряжения ơ₂ должна быть параллельна линии пересечения двух разломов, а ось ơ₁ совпадает с биссектрисой острого угла между двумя разломами (действительно, как следует из анализа в разд. 3.2.2, трещины не могут образоваться в плоскости с наклоном к оси ơ₁ более 45°).

Оцениваемое этим методом главное направление ơ₁ должно совпадать с направлением сдвига, определяемым согласно правилам, приведенным в разд. 5.5.4. Если удается провести наблюдения лишь на одном разломе, то даже приближенное определение осей ơ₁ и ơ₃ становится невозможным. Главная ось ơ₂ перпендикулярна направлению смещения, определяемому, например, по штриховке (рис. 5.19).

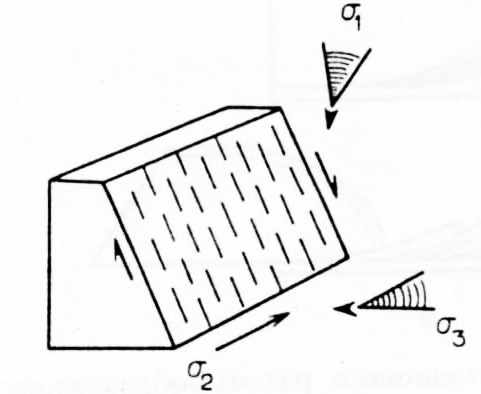
Рис. 5.19. Приблизительные направления главных нормальных напряжений в плоскости разлома с известным смещением

В анизотропных породах ориентировку разломов можно установить по наличию кливажа или сетке трещин, частично отражающих породившее их напряженное состояние. В дальнейшем обязательно потребуется статистический анализ, особенно методы, развитые в последние годы. Эти исследования, относящиеся к активным разломам, составляют предмет неотектоники.

Продвижение разломов в сложных системах. Общая связь между разрывами. стилолитовыми трещинами, разломами и соответствующими им главными направлениями напряжений суммирована на рис. 5.20.

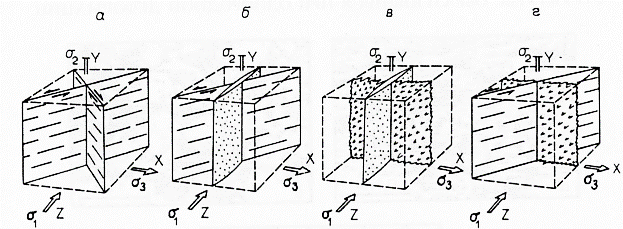
Рис. 5.20. Общие соотношения между основными структурами разрывной деформации и главными осями деформаций X, Y, Z и напряжений ơ₁, ơ₂, ơ₃: а - сопряженные секущие разломы; б - левосторонние секущие разломы и трещины растяжения; в - стилолитовая трещина и трещина растяжения; г - левосторонний секущий разлом и стидолитовая трещина (Arthaud, Choukroune. 1972, Rev. Inst. Fr. Petr., 715)

Однако существуют и другие сложные системы, связывающие различные типы трещин и разломов. Мы уже указывали на генетическую связь между трещинами растяжения и сдвигами (рис. 5.8). Сдвигообразование в изотропной среде, как показано на рис. 5.15 и 5.21, также может развиваться в результате совместного развития разрывов разного типа. Для понимания этих особенностей лучше всего обратиться к тщательному изучению связи между напряжениями и разрывообразованием.

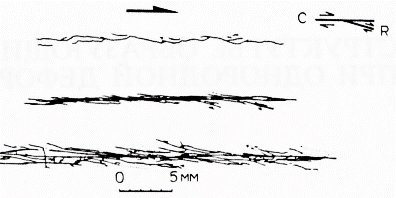
Рис. 5.21. Экспериментальный сдвиг в известняке при всестороннем давлении 500 МПа с образованием сдвигов второго порядка R по мере роста деформации (сверху вниз смешения составляют 0.14; 0.26 и 0.54 см) (Bartlett et al„ 1981, Tectonophysics, 79, 255)

Наличие разлома порождает анизотропию, которая влияет на локальное распределение напряжений (в частности, ơ₁ и ơ₃) на концах разлома, т е. в области его продвижения. В полуплоскости, находящейся в условиях растяжения, направление оси ơ₁ непрерывно изменяется и стремится к перпендикулярному положению относительно плоскости разлома (рис. 5.22).

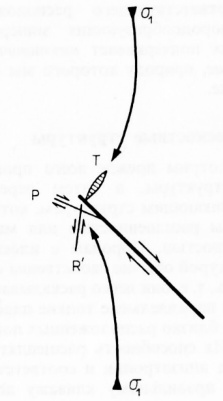
Рис. 5.22. Схематический поворот траекторий ơ₁ в окрестности разлома с зарождением трещин второго порядка Т, Р, R' в областях соответственно растяжения и сжатия

Направление оси ơ₂ теоретически не меняется, поскольку деформация является плоской. Этим же объясняется то, что линзы, образующиеся в кулисообразных трещинах растяжения, как показано на рис. 5.5, не параллельны главному направлению (биссектрисе острого угла между двумя зонами сдвига). Их ориентировка контролируется локальным поворотом оси ơ₁ в окрестности зоны разломов. Вероятно, по тем же причинам зоны сдвига на концах расщепляются на многочисленные ветви (рис. 8.16). Итак, образование магистрального разлома сопровождается появлением трещин второго порядка, ориентировка которых схематически показана на рис. 5.23. Последние могут быть сдвиговыми трещинами или зонами сдвига (рис. 8.16, б), а также оперяющими трещинами растяжения (рис. 5.8, я).

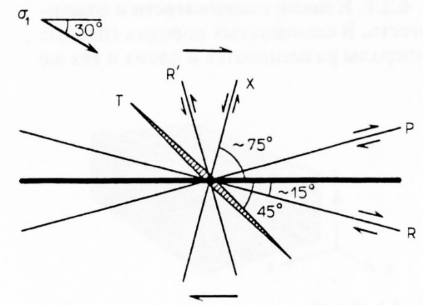
Рис. 5.23. Картина трещиноватости второго порядка в связи с правосторонним разломом (жирная линия)

Этот анализ соответствует результатам экспериментальных исследований сдвигообразования в аргиллитовом слое. Такая модель, согласно Риделю, показана на рис. 5.23. Разломы второго порядка R и R’ располагаются соответственно под углами — (5°-25) и + (95 - 115°) к главному правостороннему разлому со средними значениями углов — 15° и +105°, причем знаки углов указаны в тригонометрическом смысле. Трещины растяжения Т составляют с плоскостью главного разлома угол, приблизительно равный +135°. Наконец, могут существовать симметрично расположенные к R и R' разломы второго порядка Р и X.

Эти разломы активизируются в разное время. Если приложенные напряжения вызывают раскрытие главной зоны разлома, то преимущественно оживают системы разломов Р, X и Т (рис. 5.15, а). При сжатии этой зоны активизируется система R и R'. Первая из этих ситуаций возникает в основном тогда, когда напряжение ơ_n (разд. 2.3.2) в плоскости разлома сравнительно мало, что достигается либо при малом всестороннем давлении (как в случае приповерхностного разломообразования), либо при малом эффективном давлении (из-за высокого давления флюида); возможна и такая ситуация, когда разлом проходит по ранее существовавшей плоскости анизотропии вблизи направления ơ₁ (как на рис. 2.15, где ơ_n мало по сравнению с ơ₁). Вторая из указанных выше ситуаций, однако, преобладает в глубоких и сухих разломах или в случаях, когда угол между разломом и осью ơ₁ достаточно велик.

Рекомендуемая литература:
1. Mercier J L. La neotectonique, ses methodes et ses buts. Un exemple: l’arc egeen (Mediterranee orientale). Rev. Geogr. phys. geol. dyn., XVIII, 323, 1976.
2. Turcctte D. L„ Schubert G. Geodynamics. John Wiley, New York, 450 p., 1982