Виды передачи теплоты
Теория теплообмена изучает закономерности распространения и пе-реноса тепловой энергии. Обмен энергией в форме теплоты происходит при наличии разности температур между отдельными телами или частями одного и того же тела и продолжается до тех пор, пока температура обоих тел не сравняется. Поскольку температура является мерой внутренней энергии, следовательно, при теплообмене происходит увеличение внут-ренней энергии одного (холодного) тела за счет ее уменьшения у другого тела (горячего).
Процесс теплообмена является естественным и необратимым, т. е. он всегда протекает в одном направлении: от горячего тела к холодному.
Существует три способа переноса теплоты: теплопроводность, кон-векция и излучение.
Теплопроводность—процесс распространения теплоты в твердыхтелах и жидкостях, находящихся в состоянии покоя. В диэлектриках (в ма-териалах, непроводящих электричество) тепловая энергия передается ко-лебаниями кристаллической решетки, а в металлах — главным образом за счет движения свободных электронов в решетке. Теплопроводность в чис-том виде наблюдается только в твердых телах.
Конвекция—перенос теплоты при перемещении отдельных масс иобъемов жидких и газообразных тел.
Обычно происходит одновременно конвекция и теплопроводность. Такой процесс называется конвективным теплообменом. Перенос теплоты от одного тела к другому при конвекции и теплопроводности осуществля-ется только при их соприкосновении.
Излучение—теплообмен между телами на расстоянии в форме лу-чистой энергии. Носителями лучистой энергии являются электромагнит-ные волны (фотоны). При излучении тепловая энергия нагретого тела пе-реходит в лучистую, распространяется в окружающем пространстве, пада-ет на другое тело и вновь переходит в тепловую энергию.
Решение задач теплообмена всегда имеет конкретный характер, одно-значно определяемый условиями протекания процессов.
Эти условия включают:
– геометрические особенности поверхностей тел и окружающего их пространства (формы, размеры);
– особенности протекания процесса во времени;
– граничные особенности процесса теплообмена, т. е. значение и рас-пределение физических величин на границах раздела тел, участвующих в теплообмене;
– физические и химические свойства и параметры среды, в которой осуществляется перенос теплоты.
Не всегда, однако, эти условия однозначности позволяют получить аналитическое решение задач теории теплообмена. Поэтому для изучения процессов теплообмена исключительное значение имеют физические экс-перименты и обобщение их результатов.
Теплопроводность
Особенности явлений теплопроводности связаны с распределением температуры в телах. В общем случае температура тел может изменяться во всех точках пространства с течением времени. Совокупность мгновен-ных значений температуры во всех точках изучаемого пространства носит название температурного поля.
Температурное поле является однородным, если во всех точках про-странства температура одинакова, и неоднородным, если она различна. Поверхности, на которых расположены точки с одинаковой температурой, называются изотермическими, а сечение этих поверхностей — изотерма-ми (рис. 3.1).Вдоль изотермических поверхностей теплота не распростра-няется. Наиболее быстрое изменение температуры происходит в направле-нии по нормали к изотермическим поверхностям.
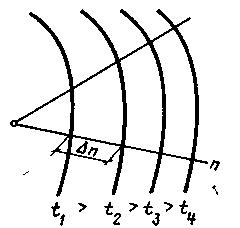
Рис. 3.1. Температурное поле
Предел отношения разности температур двух изотерм к расстоянию между ними по нормали, когда n стремится к нулю, называется градиен-
том температур и обозначаетсяgrad t.
Градиент — мера наибольшей интенсивности изменения температу-ры; он является векторной величиной. Положительным считается направ-ление, в котором температура возрастает. Количественно интенсивность теплообмена характеризуется плотностью теплового потока, то есть ко-личеством теплоты, проходящей через единицу поверхности в единицу времени. Согласно закону Фурье — основному закону теплопроводно-сти — плотность теплового потока, Вт/м2, определяется по формуле

где Q — количество теплоты, Дж; F — площадь, м2; τ — время, ч.
Закон Фурье утверждает, что плотность теплового потока пропорцио-нальна градиенту температур

где λ — коэффициент теплопроводности, характеризующий интенсивность распространения теплоты, т. е. количество теплоты, проходящее вследст-вие теплопроводности в единицу времени через единицу поверхности теп-лообмена при падении температуры на 1 градус на единицу длины норма-ли к изотермической поверхности, Вт/м К.
Знак «минус» в правой части указывает на противоположность на-правлений теплового потока и изменения температуры в теле. Коэффици-ент теплопроводности зависит от химического состава тел, их структуры, плотности, влажности, давления, температуры и составляет величину по-рядка от 0,01 до 400 Вт/(м·К).
Тела, имеющие λ<0,2 Вт/(м·К), называются теплоизоляторами. Хо-рошими проводниками теплоты являются тела, имеющие λ >20 Вт/(м·К).
Наименьшие значения коэффициента теплопроводности имеют газы (от 0,01 до 1 Вт/(м·К)), наибольшие — металлы (серебро — 410, медь —
360, алюминий — 200-300, сталь — 45-55 Вт/(м·К)).
Уравнение теплопроводности Фурье представляет собой математиче-ское описание процесса изменения температуры во времени в любом месте тела, вызываемого результирующим переносом теплоты.
Уравнения теплопроводности обычно аналитически решают для кон-кретных условий протекания процесса с привлечением известных условий однозначности.
На практике приходится встречаться с различными задачами тепло-проводности, которые условно делятся на три группы:
1) стационарная теплопроводность, когда распределение температур в теле сохраняется неизменным во времени и соответственно плотность теп-лового потока постоянна. Процессы теплообмена в нагревательных уст-ройствах и аппаратах, ограждающих конструкциях строительных соору-жений при длительных неизменных температурах наружной и внутренней среды могут рассматриваться не зависящими от времени;
2) нестационарная теплопроводность, когда происходит изменение температурного поля во времени. Нестационарная теплопроводность на-блюдается, например, при нагревании и охлаждении тел, когда до начала теплового воздействия во всей массе тела была одинаковая температура;
3) температурные волны в телах, подвергаемых периодическому теп-ловому воздействию. Например, годовые колебания температуры в по-верхностном слое земли, суточные колебания температуры наружного воз-духа и под их воздействием температуры поверхностей ограждающих кон-струкций.
Ниже дано частное решение уравнения Фурье для двух задач стацио-нарной теплопроводности.
1. Одномерное распределение теплоты в плоской стенке (рис. 3.2). Тепловой поток в плоской стенке равен

| где δ — толщина стенки, м; | tF , | tF | — граничные температуры на поверх- |
ностях F1 и F2, °С.
Для многослойной стенки с толщинами слоев δi и коэффициентами теплопроводности λi уравнение теплового потока обобщается следующим образом:


где α — коэффициент конвективной теплоотдачи, характеризующий ин-тенсивность теплообмена конвекцией, Вт/(м2·К); tж — температура жидко-сти вдали от стенки, °С; tст — температура поверхности стенки, °С; F —тепловоспринимающая поверхность тела,м2.
Одной из главных задач теории конвективного теплообмена является определение значения коэффициента теплоотдачи для конкретных условий протекания процесса.
На величину α оказывает влияние множество факторов, основными из которых являются характер конвекции, режим движения, физические свойства жидкости, геометрические особенности поверхности тел, участ-вующих в теплообмене.
Конвекция называется свободной, если она возникает за счет разности давлений (плотности), обусловленной неоднородностью температурного поля жидкости. Явление свободной конвекции можно наблюдать над по-верхностью нагретых тел, когда находящиеся вблизи этих поверхностей частицы воздуха, нагреваясь, поднимаются вверх, а на их место устремля-ются холодные массы воздуха (рис. 3.4).
Свободная конвекция возникает естественно во всяком объеме, где имеются тела с различной температурой, и протекает тем интенсивнее, чем выше разность температур.
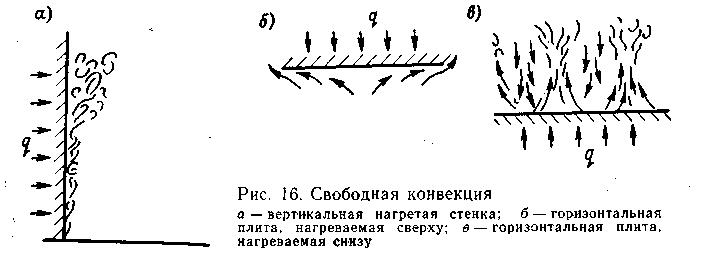
а) б) в)
Рис . 3.4. Свободная конвекция: а – вертикальная нагре-тая стенка; б – горизонтальная плита; в – горизонталь-ная плита, нагреваемая снизу
Вынужденной конвекцией называется теплообмен при движении жид-кости под действием внешних сил, например, создаваемых насосом, вен-тилятором, компрессором. Интенсивность теплообмена при этом тем вы-ше, чем больше скорость течения жидкости, омывающей поверхности тел.
Причина повышения интенсивности теплообмена при увеличении скорости течения заключается в изменении режима движения жидкости, переходе ламинарного движения в турбулентное (см. рис. 3.1).
В ламинарном потоке тепловая энергия переносится тепло-проводностью и поперечной диффузией масс. Интенсивность такого переноса энергии зависит от свойств среды, и тем меньше, чем больше толщи-на потока. В турбулентном потоке энергия переносится от жидкости к стенке перемешивающимися массами и лишь в пограничном слое — теп-лопроводностью. Поэтому интенсивность теплоотдачи в турбулентном по-токе выше, чем в ламинарном.
Ламинарное и турбулентное течения жидкости могут наблюдаться как при вынужденном, так и при свободном движении. Однако в последнем случае эти режимы создаются исключительно условиями теплового воз-действия, тогда как при вынужденном движении используются искусст-венные способы воздействия на течение жидкости.
Интенсивность конвективной теплоотдачи зависит также от физиче-ских свойств жидкости, характеризуемых значением коэффициентов теп-лопроводности и температуропроводности, теплоемкости, коэффициентов объемного расширения и кинематической вязкости.
Геометрические условия конвективного теплообмена определяются формой тела, его размерами, характером поверхности, обтекаемой жидко-стью.
По геометрическим условиям различают теплообмен при внутреннем течении жидкости в трубах, каналах (внутренняя задача) и внешнем омы-вании поверхностей потоком (внешняя задача). При внешнем обтекании поток может быть продольным по отношению к наибольшему размеру по-верхности или поперечным (например, при обтекании пучка труб, располо-женных перпендикулярно направлению потока).
Во всех случаях геометрические условия оказывают существенное влияние на распределение скоростей и температур в потоке, на режим движения, изменяя интенсивность теплообмена. Для учета этих факторов необходимо задаваться характерными размерами и формой тела.
Значения коэффициентов теплоотдачи в различных задачах конвек-тивного теплообмена определяют путем решения критериальных уравне-ний, при помощи которых обобщаются данные экспериментальных иссле-дований, так, например, для свободной конвекции используется уравнение вида
| Nu = С (Gr Рr)n; | (3.8) |
| для вынужденной конвекции | |
| Nu = С Rеm Рrn, | (3.9) |
где Nu l —критерий Нуссельта; α —коэффициент конвективной теп-
| лоотдачи, Вт/(м2·К); l — характерный геометрический | размер, м; | |||
| λ —коэффициент теплопроводности,Вт/(м·К); Gr | gl 3 | t | — критерий | |
| 2 | ||||
Грасгофа; g — ускорение силы тяжести, м/с2; β — коэффициент объемного
| расширения, 1/К; | — коэффициент кинематической | вязкости, м2/с; | |||||
| t —разность | температур, K; Pr | — | критерий Прандтля; | ||||
| a | |||||||
| а —коэффициент температуропроводности,м2/с; | Re | l — критерий | |||||
Рейнольдса; С, n, m — опытные коэффициенты, — скорость жидкости, м/с.
Дата добавления: 2016-06-15; просмотров: 11404;











