Закон больших чисел

Лемма (Чебышев). Если случайная величина ξ имеет конечную дисперсию D_x, то имеет место следующее неравенство:

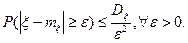(1)

Доказательство.

Пусть f(x) - плотность распределения случайной величины ξ.

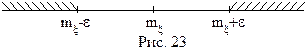
Тогда

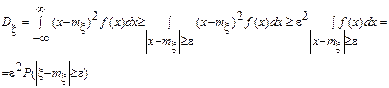
(см. рис. 23).

Разделив последнее неравенство на ε², получим (1). Лемма доказана.

Замечание.Неравенство (1) можно записать в виде

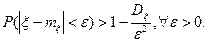(1^¢)

Определение. Последовательность случайных величин ξ₁,ξ₂,…,ξ_n,… называется сходящейся по вероятности к величине ξ₀ при n→ ∞, если для любого e>0 имеет место равенство 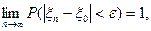что эквивалентно равенству 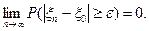Пишут 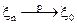при n→ ∞.

Теорема (Чебышев). Если все члены последовательности ξ₁, ξ₂,…, ξ_n,… имеют равномерно ограниченные дисперсии, т.е. 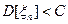, и являются попарно независимыми, то имеет место равенство

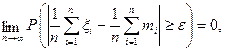(2)

т.е. среднее арифметическое случайных величин сходится по вероятности к среднему арифметическому их математических ожиданий.

Доказательство. Рассмотрим величину 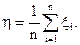Найдем ее математическое ожидание и дисперсию

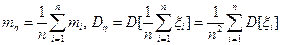(см. (5) §20). Т.к. 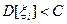, то 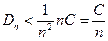, т.е. дисперсия D_η - величина ограниченная. Тогда по лемме Чебышева

, " e> 0, или

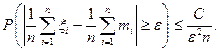
Переходя к пределу в последнем соотношении, получим (2), т.к. вероятность не может быть отрицательной.

Замечание. Если последовательность ξ₁,ξ₂,…,ξ_n,… есть результат измерения одной и той же величины ξ_, то все ξ_i имеют один и тот же закон распределения, совпадающий с законом распределения ξ.

Тогда

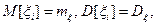
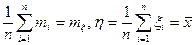
– среднее арифметическое n измерений. Теорему Чебышева в этом случае можно записать так: 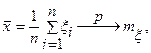т.е. среднее арифметическое n измерений сходится по вероятности к математическому ожиданию измеряемой величины. Поэтому среднее арифметическое 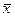может служить хорошей оценкой математического ожидания. Такие оценки называют состоятельными.

Следствие. Пусть случайная величина ξ_i означает число появлений события А в i-ом испытании Бернулли. Тогда она имеет следующий ряд распределения:

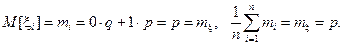
Величина 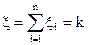есть общее число появлений событий А в n испытаниях, а 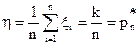- частота появления события А в n испытаниях. Равенство (2) в этом случае запишется так:

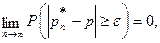(3)

или 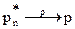при n→ ∞, т.е. частота появления события стремится к вероятности этого события. Об этом говорилось в §2. Равенство (3) называют теоремой Бернулли.

Теоремы Чебышева и Бернулли выражают так называемый закон больших чисел, который устанавливает факт сходимости статистических характеристик к соответствующим теоретическим характеристикам.

Пример 1. Вероятность наступления события А в каждом испытании p=0,3. Оценить вероятность того, что в 10 тыс. испытаниях отклонение частоты 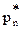события А от вероятности этого события не превысит 0,01 по абсолютному значению.

Решение. Следует оценить величину 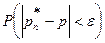при ε=0,01. Согласно (1^¢)

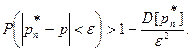(4)

Если ξ – число появлений события А в n=10⁴ испытаниях, то 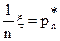- частота, D_ξ=npq=10⁴×0,3×0,7=2100 - дисперсия. Найдем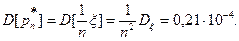

Подставляя данные значения в (4), получим 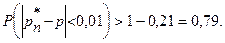Таким образом, искомая вероятность не меньше, чем 0,79.