Закон распределения функции случайного аргумента
В предыдущем параграфе отмечено, что по известному закону распределения аргумента всегда можно найти закон распределения функции. Остановимся на этом подробнее.
Пусть случайные величины h и 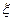 связаны функциональной зависимостью
связаны функциональной зависимостью 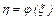 и пусть
и пусть 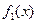 - известная плотность распределения случайной величины
- известная плотность распределения случайной величины 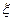 , а
, а 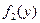 - искомая плотность распределения случайной величины h. Запишем сначала условную плотность распределения
- искомая плотность распределения случайной величины h. Запишем сначала условную плотность распределения 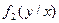 случайной величины h относительно
случайной величины h относительно 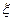 . Поскольку при всяком возможном значении x случайной величины
. Поскольку при всяком возможном значении x случайной величины 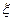 случайная величина h принимает единственное значение y с вероятностью 1, то очевидно
случайная величина h принимает единственное значение y с вероятностью 1, то очевидно
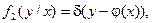 (1)
(1)
где d (x) – дельта-функция. Тогда совместная плотность распределения величин 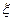 и h запишется так (см. (4) §15):
и h запишется так (см. (4) §15):
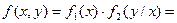
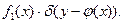
А плотность распределения случайной величины h определяется формулой
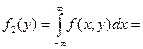
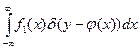 (2)
(2)
(см. (4) §14).
Формула (2) является общей формулой, определяющей закон распределения функции, если известен закон распределения ее аргумента. Она справедлива и в том случае, когда 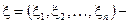 случайный вектор, т.е. функция y = j (x),
случайный вектор, т.е. функция y = j (x), 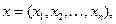 является функцией n переменных. В этом случае под dx следует понимать dx1, dx2,¼, dxn, а интеграл (2) считать n – кратным.
является функцией n переменных. В этом случае под dx следует понимать dx1, dx2,¼, dxn, а интеграл (2) считать n – кратным.
Пример 1.Найти плотность распределения случайной величины 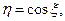 если
если 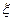 равномерно распределена на отрезке
равномерно распределена на отрезке 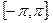
Решение.Поскольку 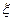 распределена равномерно, то
распределена равномерно, то
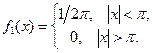
Воспользуемся формулой (2).
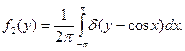
В интеграле сделаем замену 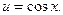 Тогда
Тогда 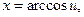
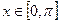 и
и 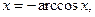
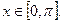 Учитывая это и свойство d - функции (см. §2 гл.4), получим
Учитывая это и свойство d - функции (см. §2 гл.4), получим
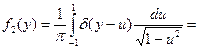
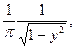
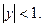
Пример 2.Найти плотность распределения произведения случайных величин 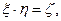 если плотность f(x,y) двумерной случайной величины (
если плотность f(x,y) двумерной случайной величины ( 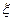 ,h) известна.
,h) известна.
Решение.Воспользуемся формулой (2). Получим
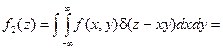
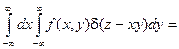
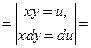
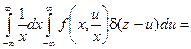
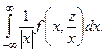
Дата добавления: 2020-02-05; просмотров: 805;











