Из определения вычета следует
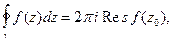 (1)
(1)
т.е, зная вычет функции 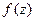 в точке
в точке 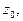 мы можем вычислить интеграл по замкнутому контуру, содержащему внутри себя только одну изолированную особую точку
мы можем вычислить интеграл по замкнутому контуру, содержащему внутри себя только одну изолированную особую точку 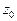 .
.
Теорема 1 (основная теорема о вычетах). Если функция 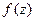 аналитическая всюду в ограниченной односвязной области
аналитическая всюду в ограниченной односвязной области 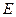 за исключением конечного числа изолированных особых точек
за исключением конечного числа изолированных особых точек 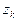 однозначного характера, то
однозначного характера, то
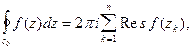 (2)
(2)
где 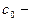 замкнутая кривая, содержащая внутри все особые точки.
замкнутая кривая, содержащая внутри все особые точки.
Доказательство. Выделим каждую особую точку замкнутым контуром 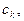 содержащим только одну особую точку
содержащим только одну особую точку 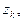 и воспользуемся теоремой 2 §6. В результате получим
и воспользуемся теоремой 2 §6. В результате получим 


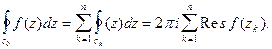
Теорема доказана.
Следствие.Если функция f(z) аналитическая во всей расширенной комплексной плоскости за исключением конечного числа особых точек, то сумма всех вычетов функции f(z), включая и вычет в точке z = ¥, равна нулю, т. е.
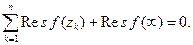 (3)
(3)
Здесь zk – конечные особые точки.
Доказательство.Пусть z = R ¹ ¥ - окружность, внутри которой расположены все особые точки zk. Тогда согласно теореме 1
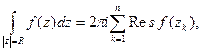 (4)
(4)
где окружность z = R обходится против стрелки часов. Однако, если ее обходить по стрелке часов, то согласно определению вычета в бесконечно удаленной точке имеем
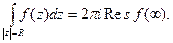 (5)
(5)
Подставляя (5) (с противоположным знаком) в (4), получим 3. Следствие доказано.
Пример 1.Вычислить интеграл 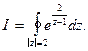
Решение.Особая точка 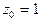 лежит внутри контура
лежит внутри контура 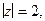 поэтому, согласно (1) или (2), получим
поэтому, согласно (1) или (2), получим 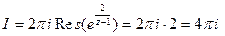 (см.(2) §8).
(см.(2) §8).
Пример 2.Вычислить интеграл 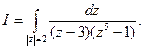
Решение.Согласно теореме 1
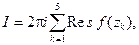
где f(z) – подынтегральная функция, а 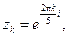
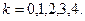 Т. к. суммирование вычетов приводит к довольно громоздким вычислениям, то воспользуемся следствием теоремы 1. Получим
Т. к. суммирование вычетов приводит к довольно громоздким вычислениям, то воспользуемся следствием теоремы 1. Получим
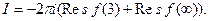
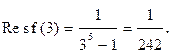
Поскольку 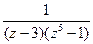 ~
~ 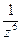 при z ® ¥, то с-1 = - Res f(¥) = 0. Итак,
при z ® ¥, то с-1 = - Res f(¥) = 0. Итак,
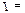
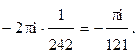
При вычислении контурных интегралов от однозначной ветви многозначной аналитической функции нужно следить за тем, чтобы вычеты брались от нужной ветви.
Пример 3.Вычислить интеграл 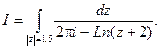
Решение.
В круге ½z½< 1,5 можно выделить однозначную ветвь функции Ln(z + 2). Таких ветвей бесконечное множество и они задаются формулой
Ln(z + 2) = ln½z + 2½+ iarg(z + 2) + 2p ki, k Î Z.
Приравнивая знаменатель подынтегральной функции к нулю, получим
ln(z + 2) + iarg½z + 2½+ 2p ki = 2 p i Þ z0 = -1,  k = 1.
k = 1.
Таким образом, если взять ту ветвь, которая в точке z0 = -1 равна 2p i, то подынтегральная функция будет иметь простой полюс в точке z0 = -1. Согласно (1) получим

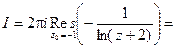
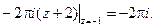
Все остальные ветви (при k ¹ 1) являются аналитическими функциями в круге ½z½< 1,5, поэтому I = 0.
Определенный интеграл 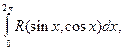 где
где 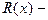 дробно рациональная функция, с помощью замены
дробно рациональная функция, с помощью замены 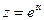 сводится к интегралу по замкнутому контуру от функции комплексного переменного, который можно вычислить с помощью вычетов.
сводится к интегралу по замкнутому контуру от функции комплексного переменного, который можно вычислить с помощью вычетов.
Пример 4.Вычислить 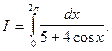
Решение. 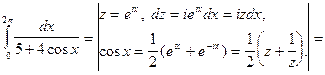
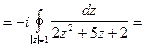
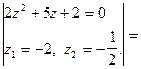
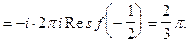
Рассмотрим вычисление несобственного интеграла 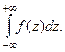
Лемма 1.Пусть  функция
функция 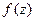 аналитическая в верхней полуплоскости
аналитическая в верхней полуплоскости 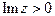 всюду за исключением конечного числа изолированных особых точек. Если в точке
всюду за исключением конечного числа изолированных особых точек. Если в точке 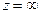 функция
функция 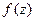 имеет нуль не ниже второго порядка, то
имеет нуль не ниже второго порядка, то
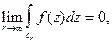
 (6)
(6)
где 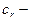 верхняя часть окружности
верхняя часть окружности 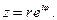
Доказательство.Очевидно, 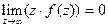 или
или 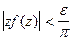 при
при 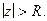 На окружности
На окружности 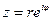 получим
получим 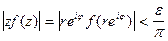 при
при 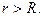 Оценим интеграл
Оценим интеграл 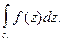


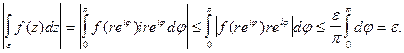
Итак, 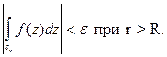 Это означает, что (6) выполняется, и лемма доказана.
Это означает, что (6) выполняется, и лемма доказана.
Теорема 2.Если функция 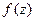 удовлетворяет условиям леммы1, то главное значение несобственного интеграла можно найти по формуле
удовлетворяет условиям леммы1, то главное значение несобственного интеграла можно найти по формуле
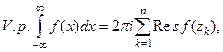 (7)
(7)
где 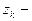 особые точки в верхней полуплоскости.
особые точки в верхней полуплоскости.
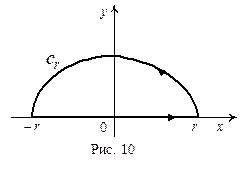
Доказательство: 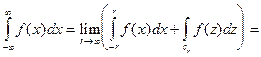
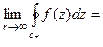
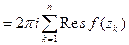 (см. рис. 10).
(см. рис. 10).
Воспользовались леммой 1 и теоремой 1. Теорема доказана.
Замечание.Если функция 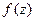 имеет только простые полюса на действительной оси, то к вычетам (7) следует добавить вычеты в этих полюсах, уменьшенные в два раза.
имеет только простые полюса на действительной оси, то к вычетам (7) следует добавить вычеты в этих полюсах, уменьшенные в два раза.
Пример 5. Вычислить интеграл 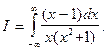
Решение.
Рассмотрим функцию комплексного переменного 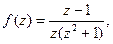 которая на действительной оси совпадает с подынтегральной функцией. Она называется аналитическим продолжением функции f(x) с действительной оси на комплексную плоскость. Функция f(z) удовлетворяет лемме 1, поэтому согласно (7) и замечанию, получим
которая на действительной оси совпадает с подынтегральной функцией. Она называется аналитическим продолжением функции f(x) с действительной оси на комплексную плоскость. Функция f(z) удовлетворяет лемме 1, поэтому согласно (7) и замечанию, получим 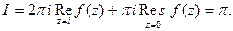
Лемма 2 (Жордан).Пусть функция 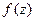 является аналитической во всей комплексной плоскости за исключением конечного числа изолированных точек и равномерно относительно
является аналитической во всей комплексной плоскости за исключением конечного числа изолированных точек и равномерно относительно 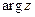 стремится к нулю при
стремится к нулю при 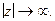 Тогда
Тогда
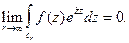 (8)
(8)
Здесь 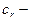 верхняя часть окружности
верхняя часть окружности 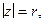 если
если 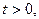 и нижняя, если
и нижняя, если 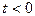 (без доказательства).
(без доказательства).
Теорема 3. Если функция 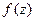 удовлетворяет лемме 2, то
удовлетворяет лемме 2, то
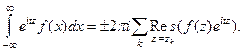 (9)
(9)
Знак плюс в (9) берется, если 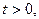 а особые точки
а особые точки 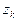 в верхней полуплоскости. Знак минус - если
в верхней полуплоскости. Знак минус - если 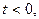 а
а 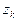 в нижней полуплоскости.
в нижней полуплоскости.
Доказать теорему 3 самостоятельно, см. доказательство теоремы 2.
Замечание к теореме 2 справедливо и для теоремы 3.
Пример 6.Вычислить 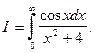
Решение. 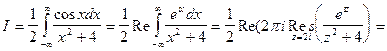
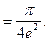
Лемма 3 (Жордан).Если функция 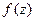 аналитическая во всей комплексной плоскости за исключением конечного числа изолированных точек и равномерно относительно
аналитическая во всей комплексной плоскости за исключением конечного числа изолированных точек и равномерно относительно 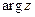 стремится к нулю при
стремится к нулю при 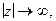 то
то
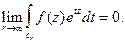 (10)
(10)
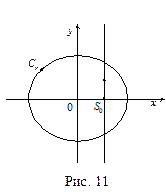
Здесь 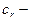 часть окружности
часть окружности 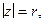 для точек которой выполняется неравенство
для точек которой выполняется неравенство 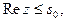 если
если 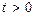 (см. рис. 11). Если
(см. рис. 11). Если 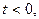 то
то 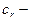 другая часть этой же окружности, для точек которой
другая часть этой же окружности, для точек которой 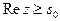 (без доказательства).
(без доказательства).
Лемма 3 дает возможность вычислять с помощью вычетов несобственные интегралы вида 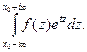 (11)
(11)
|
Пример 7.Вычислить интеграл 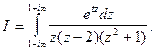
Решение.Функция 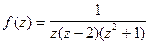 удовлетворяет лемме 3. Точки
удовлетворяет лемме 3. Точки 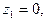
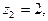
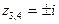 являются полюсами этой функции. Пусть
являются полюсами этой функции. Пусть 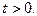
|
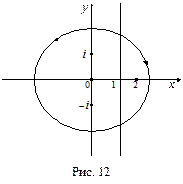
Тогда, замыкая контур интегрирования влево (см. рис. 12) и пользуясь основной теоремой о вычетах, получим
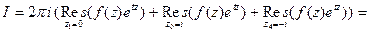
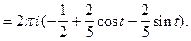
При 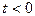 контур интегрирования замыкаем вправо. В результате получим
контур интегрирования замыкаем вправо. В результате получим
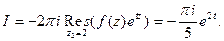
Итак, 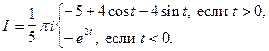
Пример 8.Вычислить интеграл 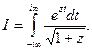
Решение.Заметим, что подынтегральная функция неоднозначная, но в правой полуплоскости можно выделить ее однозначную ветвь. Поэтому при t < 0, замыкая контур интегрирования вправо (см. рис.13) и пользуясь леммой 3, получим I = 0.
Левая полуплоскость содержит точку ветвления z0 = -1 и в ней можно выделить однозначную ветвь подынтегральной функции, если сделать разрез от точки z0 = -1 до бесконечности. (Положим, например, что аргумент значения 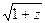 на верхнем берегу разреза равен p/2. Тогда на нижнем он будет равным -p/2). Отсюда ясно, что непосредственно воспользоваться леммой 3 при t > 0 мы не можем. Поэтому рассмотрим интеграл по замкнутому контуру, расположенному в левой полуплоскости и состоящему из шести частей, из которых с1, с3 и с5 – отрезки прямых, с2 и с6 – части окружности радиуса R с центром в нуле, а с4 – окружность радиуса r с центром в точке z0 = -1 (см. рис. 13).
на верхнем берегу разреза равен p/2. Тогда на нижнем он будет равным -p/2). Отсюда ясно, что непосредственно воспользоваться леммой 3 при t > 0 мы не можем. Поэтому рассмотрим интеграл по замкнутому контуру, расположенному в левой полуплоскости и состоящему из шести частей, из которых с1, с3 и с5 – отрезки прямых, с2 и с6 – части окружности радиуса R с центром в нуле, а с4 – окружность радиуса r с центром в точке z0 = -1 (см. рис. 13).
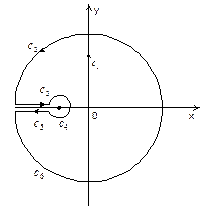
Рис.13
Внутри этого контура подынтегральная функция всюду аналитическая , поэтому интеграл равен нулю, т.е.
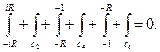
Согласно лемме 3 интегралы по контурам с2 и с6 при R®¥ стремятся к нулю. Легко показать, что интеграл по контуру с4 при r®0 также стремится к нулю, а интегралы по с3 и с5 противоположны по знаку. Таким образом, в пределе (R®¥, r®0) получим
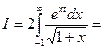
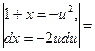
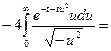
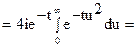
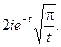
Воспользовались интегралом Пуассона (см. §3, гл.9, ч.1).
Таким образом,
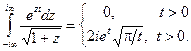
Дата добавления: 2020-02-05; просмотров: 637;











