Понятие аналитической функции
Пусть однозначная функция 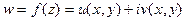 определена в некоторой окрестности точки z. Выберем точку
определена в некоторой окрестности точки z. Выберем точку 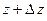 из этой окрестности, вычислим
из этой окрестности, вычислим 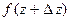 и найдем приращение функции
и найдем приращение функции 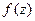 в точке z.
в точке z.
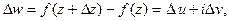 где
где 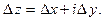
Определение 1.Если существует предел 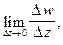 то он называется производной функции
то он называется производной функции 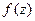 в точке z. Пишут
в точке z. Пишут
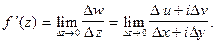 (1)
(1)
Функция, имеющая производную в точке z, называется дифференцируемой в этой точке.
Теорема 1.Если функция 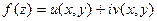 дифференцируема в точке z, то в этой точке справедливы соотношения Эйлера-Даламбера
дифференцируема в точке z, то в этой точке справедливы соотношения Эйлера-Даламбера
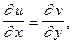
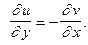 (2)
(2)
Доказательство. По условию теоремы существует предел (1), не зависящий от способа стремления 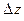 к нулю. Поэтому положим
к нулю. Поэтому положим 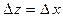 и найдем предел (1).
и найдем предел (1).
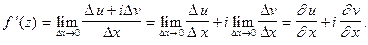 (3)
(3)
Полагая 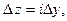 аналогично из (1) получим
аналогично из (1) получим
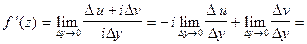
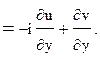 (4)
(4)
Сравнивая (3) и (4), получим (2). Теорема доказана.
Следствие. Если условия (2) не выполняются в некоторой точке, то функция 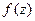 недифференцируема в этой точке. Доказательство от противного.
недифференцируема в этой точке. Доказательство от противного.
Теорема2.Если функции 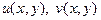 дифференцируемые в некоторой точке, а их частные производные удовлетворяют условиям (2), то функция
дифференцируемые в некоторой точке, а их частные производные удовлетворяют условиям (2), то функция 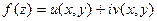 дифференцируемая в этой точке, причем производную функцию можно найти по формуле (3) или (4) (без доказательства).
дифференцируемая в этой точке, причем производную функцию можно найти по формуле (3) или (4) (без доказательства).
Пример 1. Доказать, что производная функции 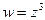 существует в любой точке
существует в любой точке 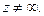
Решение. Проверим условия теоремы 2.
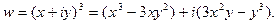
Так как функции 
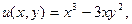
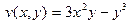 имеют непрерывные частные производные, то они дифференцируемые (см. §3 гл.6, ч.1). Найдем частные производные
имеют непрерывные частные производные, то они дифференцируемые (см. §3 гл.6, ч.1). Найдем частные производные 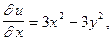
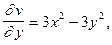
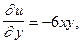
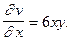 Как видно, условия (2) выполняются в любой точке
Как видно, условия (2) выполняются в любой точке 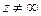 и согласно теореме 2 производная функции
и согласно теореме 2 производная функции 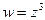 существует. Воспользуемся (3), получим
существует. Воспользуемся (3), получим
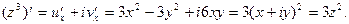 Итак,
Итак, 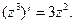
Можно убедиться, что 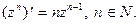
Пример 2. Найти производные функций 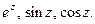
Решение.Ранее (см. §5 гл.5, ч.1) мы определяли эти функции следующим образом: 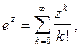
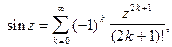
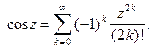
Поскольку степенные ряды можно почленно дифференцировать, то получим 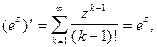
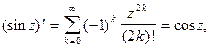

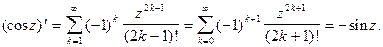
Из приведенных примеров видно, что если функция дифференцируемая, то формулы дифференцирования функции действительной переменной остаются в силе и для функции комплексного переменного. Правила дифференцирования (дифференцирование суммы, произведения и пр.) также остаются прежними.
Пример 3. Найти производную функции 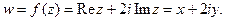
Решение. Проверим условия (2). 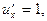
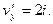 Условия (2) не выполняются ни в одной точке. Согласно следствию теоремы 1 данная функция не дифференцируемая ни в одной точке.
Условия (2) не выполняются ни в одной точке. Согласно следствию теоремы 1 данная функция не дифференцируемая ни в одной точке.
Пример 4. Найти производную функции 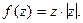
Решение.Проверим условия (2). 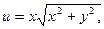
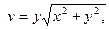
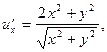
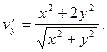 Как видно, условия (2) не выполняются для всякой точки
Как видно, условия (2) не выполняются для всякой точки 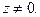 При
При 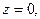 согласно определению 1, найдем
согласно определению 1, найдем
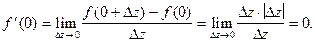
Таким образом, данная функция имеет производную только в точке 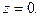
Определение 2. Однозначная функция, имеющая производную не только в данной точке, но и в некоторой ее окрестности, называется аналитической в данной точке. Функция, аналитическая в каждой точке области, называется аналитической в этой области.
Например, функции 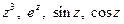 аналитические на всей комплексной плоскости
аналитические на всей комплексной плоскости 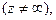 а функция
а функция 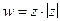 не является аналитической ни в одной точке, хотя и дифференцируемая в нуле. Функция, аналитическая во всей комплексной плоскости
не является аналитической ни в одной точке, хотя и дифференцируемая в нуле. Функция, аналитическая во всей комплексной плоскости 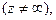 называется целой.
называется целой.
Например, 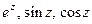 - целые функции.
- целые функции.
Многочлен 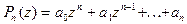 называется целой рациональной функцией. Отношение двух целых функций называется мероморфной функцией, а отношение двух многочленов называется дробно-рациональной функцией.
называется целой рациональной функцией. Отношение двух целых функций называется мероморфной функцией, а отношение двух многочленов называется дробно-рациональной функцией.
Формула Эйлера (см. (6) §2 гл.I ч.I) справедлива и для комплексного переменного z
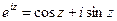 (5)
(5)
В этом легко убедиться, суммируя сначала четные, а затем нечетные члены ряда, определяющего функцию 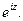
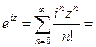
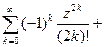
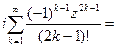
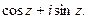
Заменяя iz в формуле Эйлера (5) на (-iz), получим
 (6)
(6)
Складывая и вычитая (5) и (6), найдем
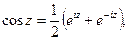
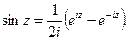 (7)
(7)
Гиперболические косинус и синус от комплексного переменного z определяются формулами
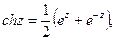
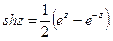 (8)
(8)
Если в формулах (7) вместо z подставить iz, то получим с учетом (8)
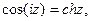
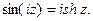 (9)
(9)
Аналогично из (9) найдем
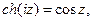
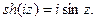
 (10)
(10)
Используя правила дифференцирования, из (8) получим производные гиперболических функций
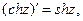
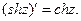 (11)
(11)
Функции 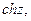
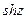 являются целыми аналитическими функциями во всей комплексной плоскости .
являются целыми аналитическими функциями во всей комплексной плоскости .
Периодичность, четность, формулы приведения, формулы от суммы для синуса и косинуса, справедливые для действительных переменных, остаются справедливыми и для комплексных переменных. Отметим только, что утверждение, что модули синуса и косинуса не превосходят единицы, для комплексного переменного уже неверно. Однако тождество 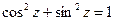 остается справедливым.
остается справедливым.
Используя формулы (9) и (10), любое соотношение между тригонометрическими функциями можно перевести в соответствующее соотношение для гиперболических функций. В частности, из соотношения 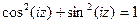 следует соотношение
следует соотношение 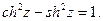
Дата добавления: 2020-02-05; просмотров: 600;











