Классификация особых точек. Вычеты

Особая точка функции 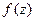называется изолированной, если существует ее окрестность, в которой нет других особых точек функции 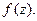Мы будем рассматривать конечные изолированные особые точки однозначного характера (не точки ветвления). Функция аналитическая в выколотой окрестности такой точки разлагается в ряд Лорана.

Определение 1.Особая точка называется устранимой, если главная часть разложения в ряд Лорана в окрестности этой точки отсутствует; полюсом, если главная часть ряда Лорана содержит конечное число членов; существенно особой, если главная часть разложения содержит бесконечное число членов.

Пример 1. 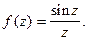Очевидно, 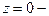особая точка.

Разложим функцию в ряд Лорана в окрестности этой точки.

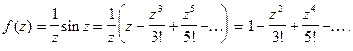
Как видно, главная часть ряда Лорана отсутствует, поэтому согласно определению точка 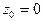является устранимой особенностью.

Пример 2. 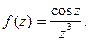Особая точка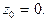

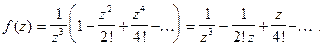
Главная часть ряда Лорана 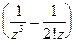содержит два члена, поэтому точка 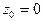является полюсом. Порядком полюса называют наибольшую степень выражения 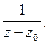В нашем случае полюс третьего порядка.

Пример 3. 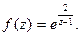Особая точка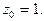

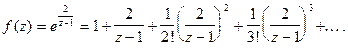
Как видно, главная часть ряда Лорана содержит бесконечное число членов, поэтому 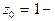существенно особая точка.

Теорема.Если предел 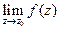конечный, то 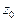является устранимой особой точкой; если предел бесконечный, то 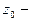полюс; если предела не существует, то 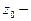существенно особая точка (без доказательства).

Упражнение.Проверить теорему на примерах 1-3.

Если 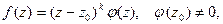т.е. точка 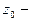нуль кратности 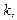то для функции 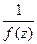эта точка является, очевидно, полюсом кратности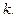

Пример 4.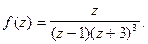

Очевидно, 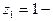простой полюс, 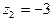- полюс третьего порядка.

Определение 2.Вычетом функции 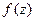в изолированной особой точке 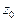называют число, определяемое интегралом

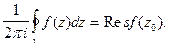(1)

Здесь 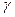- произвольный замкнутый контур, содержащий внутри себя только одну особую точку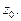

Сравнивая (1) с формулой (7) §7, видим, что 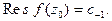Из примеров 1-3 следует, что

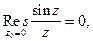
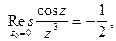
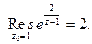(2)

Дадим более удобный метод вычисления вычета в полюсах. Пусть функция 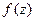имеет в точке 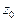полюс 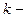го порядка.

Тогда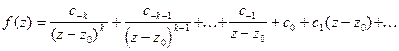

Умножим обе части последнего равенства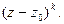

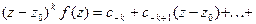
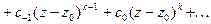(3)

Если продифференцировать равенство (3) 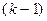раз, то свободный член в правой части будет равен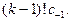

Следовательно, 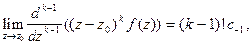или

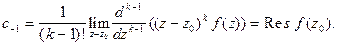(4)

В частности, если полюс простой, т.е. 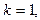то из (4) получим

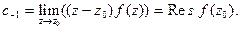(5)

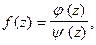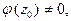
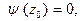
Если где 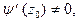т.е. точка 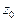является простым нулем знаменателя, то из (5) получим

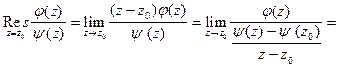
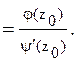(6)

Пример 5.Найти вычет функции 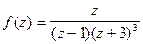в точке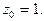

Решение.Используя (5), найдем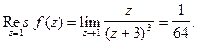

Пусть функция f(z) является аналитической в области 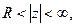т.е. в проколотой окрестности бесконечно удаленной точки. Тогда точка z = ¥ является либо особой точкой однозначного характера, либо функция f(z) в ней аналитическая.

Определение 3.Вычетом функции f(z) в точке z = ¥ называют число, определяемое интегралом

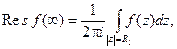(7)

где окружность 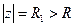обходится по часовой стрелке. Очевидно, Res f (¥) = - c_-1,

где c_-1 – коэффициент ряда Лорана функции f(z) в проколотой окрестности бесконечно удаленной точки.

Пример 6.Найти вычет в точке z = ¥ функции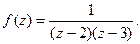

Решение.Поскольку 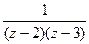~ 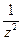при z ® ¥, то c_-1 = 0, следовательно, Res f (¥) = 0.