Ряды Тейлора и Лорана

Рядом Тейлора для функции 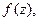как известно, называется степенной ряд

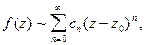(1)

коэффициенты которого определяются формулой

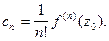(2)

Согласно теореме Абеля (см. §5 гл.5, ч.1) областью сходимости ряда (1) является круг радиуса R. При этом, если 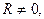то внутри круга сходимости ряд сходится к своей сумме равномерно и его можно почленно дифференцировать сколько угодно раз. Знак соответствия в (1) вместо знака равенства стоит потому, что не ясно, совпадает ли сумма ряда с функцией 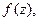для которой он формально записан. Этот вопрос проясняет следующая теорема.

Теорема 1.Если функция 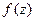аналитическая внутри круга 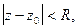то она разлагается в ряд Тейлора, т.е.

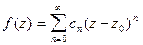(без доказательства).

Замечание 1.Используя формулу (10) §6, коэффициенты ряда Тейлора можно записать иначе 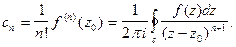(3)

Здесь с- произвольный замкнутый контур, охватывающий точку 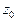и лежащий внутри круга сходимости.

Теорема 2.Всякий степенной ряд с отличным от нуля радиусом сходимости является рядом Тейлора своей суммы.

Доказательство.Пусть степенной ряд 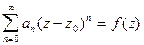сходится к своей сумме 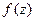в круге 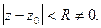Т.к. степенной ряд можно почленно дифференцировать, то для k-ой производной получим

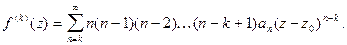
Отсюда, пр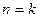и и 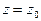найдем 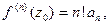или 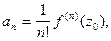что совпадает с (2). Теорема доказана.

Замечание 2.Из теоремы 2 следует, что сумма степенного ряда является функцией аналитической внутри круга сходимости.

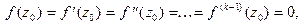
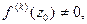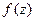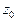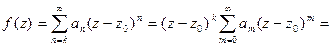
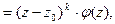
Если то ряд Тейлора функции в окрестности точки будет иметь следующий вид: 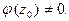(4)

Точка 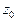в этом случае называется нулем кратности k.

Из теоремы 1 и 2 следует, что функция 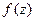будет аналитической в точке 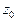только в том случае, если в окрестности точки 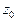она разлагается в ряд Тейлора. В противном случае функция не будет аналитической в точке 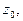и эта точка называется особой. Примерами особых точек являются точки разрыва и точки, в окрестности которых нельзя выделить однозначную ветвь функции (они называются точками ветвления). Например, для функции 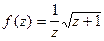особыми точками являются: точка разрыва 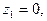точка ветвления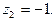

Чтобы определить характер бесконечно удаленной точки 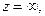делают замену 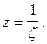Тогда точка 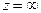отображается в точку 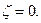При этом, если функция 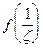аналитическая в точке 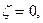то и функция 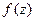аналитическая в точке 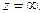Если 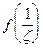имеет особенность при 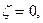то такую же особенность имеет функция 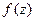при 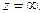В нашем примере 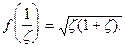В точке 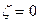функция 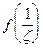имеет точку ветвления, следовательно функция 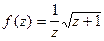в точке 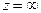имеет точку ветвления.

Определение.Ряд 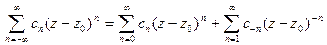(5)

называется рядом Лорана.

Первая его часть 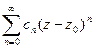называется регулярной частью, а вторая 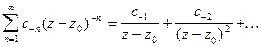называется главной частью ряда Лорана.

Регулярная часть является степенным рядом и область его сходимости - некоторый круг 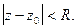В главной части сделаем замену 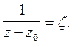Тогда относительно 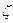получим степенной ряд 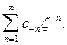Областью его сходимости также является некоторый круг 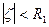или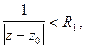

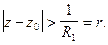
Если 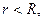то общей областью сходимости регулярной и главной частей ряда Лорана является кольцо 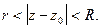Итак, областью сходимости ряда Лорана (5) является кольцо.

Теорема 3.Если функция 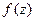аналитическая в кольце 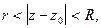то она разлагается в ряд Лорана

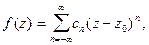(6)

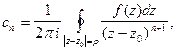
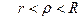(7)

(без доказательства).

Если 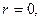то кольцо превращается в круг радиуса 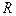с выколотым центром. Если функция 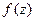аналитическая в этом круге, но неаналитическая в точке 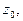то ряд (6) в этом случае называется рядом Лорана функции 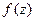в окрестности особой точки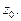

Пример.Разложить функцию 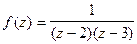в ряд Лорана.

Решение.Функция 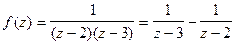аналитическая во всей комплексной плоскости, исключая точки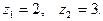

1. Рассмотрим круг 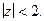В нем функция 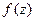аналитическая и согласно теореме 1 разлагается в ряд Тейлора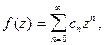

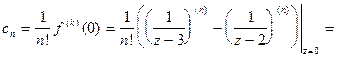
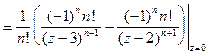
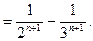
2. В кольце 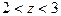данная функция аналитическая и поэтому, согласно теореме 3, разлагается в ряд Лорана

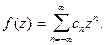
Найти коэффициенты 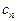по формуле (7) не просто. Лучше воспользоваться формулой суммы бесконечно убывающей геометрической прогрессии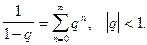

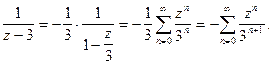(8)

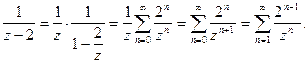(9)

Вычитая из (8) (9), получим ряд Лорана

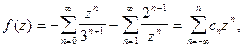
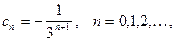
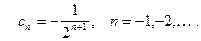
3. В области 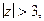т.е. в окрестности бесконечно удаленной точки аналогично получим следующий ряд Лорана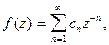 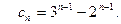Убедиться в этом самостоятельно.