Дифференциальный и интегральный законы распределения
Закон распределения случайной величины устанавливает связь между возможными значениями этой величины и соответствующими этим значениям вероятностям их появления. Существует две формы описания закона распределения случайной величины - дифференциальная и интегральная. Причем, в метрологии в основном используется дифференциальная форма - закон распределения плотности вероятностей случайной величины.
Дифференциальный закон распределения характеризуется плотностью распределения Плотность распределения случайной величины в данном случае вероятность P попадания случайной величины в интервал от x1 до x2 :
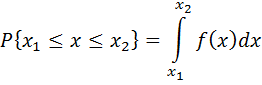 Графически эта вероятность представляет собой отношение площади под кривой f(x) в интервале от x1 до x2 к общей площади, ограниченной всей кривой распределения.
Графически эта вероятность представляет собой отношение площади под кривой f(x) в интервале от x1 до x2 к общей площади, ограниченной всей кривой распределения.
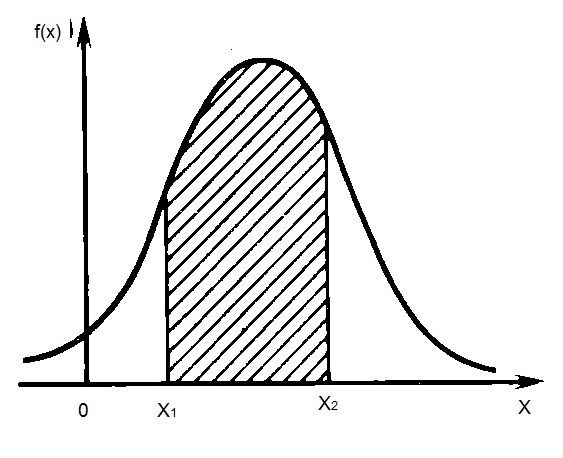
В данном случае представлено распределение непрерывной случайной величины. Кроме них существуют и дискретные случайные величины, принимающие ряд определенных значений, которые можно пронумеровать.
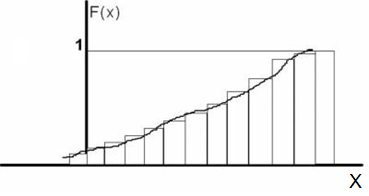
Интегральный закон распределения случайной величины представляет собой функцию F(x), определяемую формулой
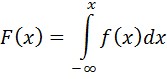
Вероятность, что случайная величина будет меньше х1 дается значением функции F(х) при х = х1 :
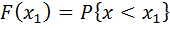
F(X) – функция неубывающая и при X → ∞ F(X)→1
При X → - ∞ F(X)→0
F(x) - функция непрерывная, т.к. результат наблюдений в определенном интервале может принять любое значение
Однако четвертое свойство обычно на практике не реализуется. Это обусловлено тем, что применяемые СИ имеют конечное разрешение: для стрелочного прибора - это цена деления шкалы (квант ФВ), для цифровых приборов - это цена наименьшего разряда кода. Поэтому реально функция распределения для погрешности имеет ступенчатый вид.
Тем не менее в метрологической практике интегральную функцию считают непрерывной, что упрощает обработку погрешностей.
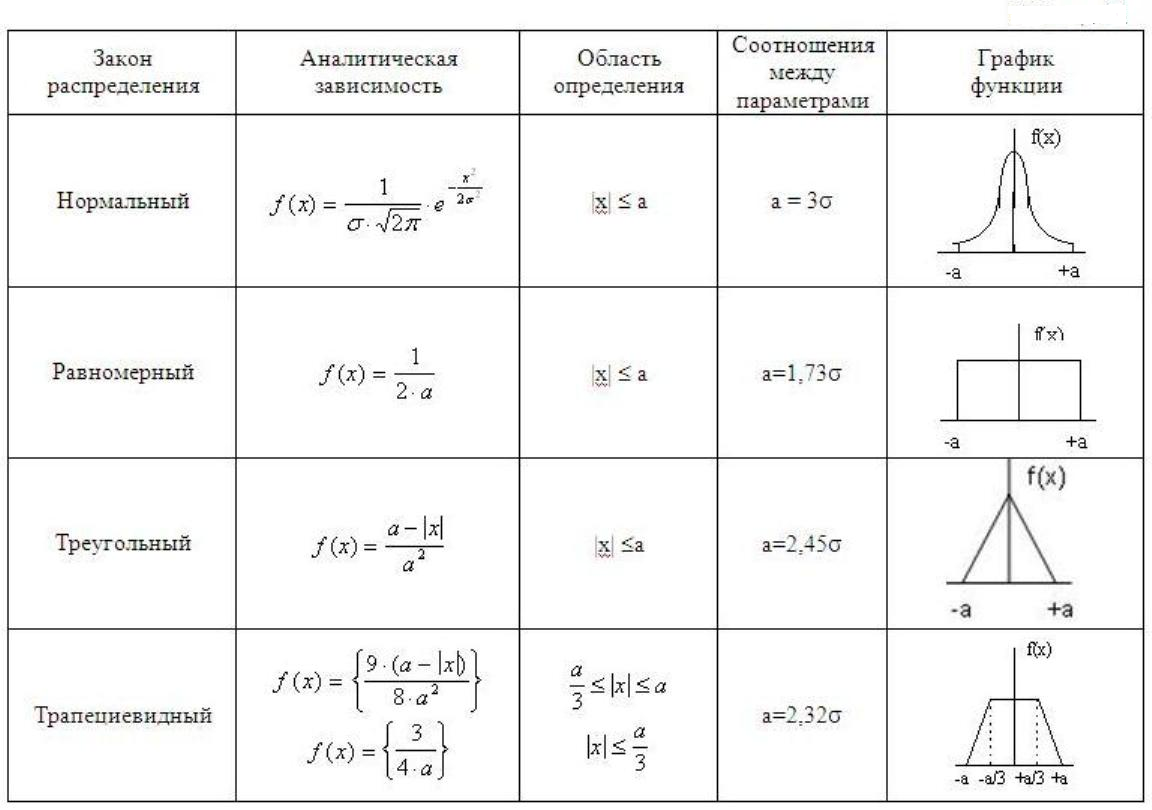
Равномерный закон распределения непрерывной случайной величины.
Непрерывная случайная величина подчиняется равномерному закону распределения, если её возможные значения лежат в некотором определённом интервале, в пределах которого все значения равновероятны, то есть обладают одной и той же плотностью вероятности. Другими словами, распределение вероятностей называют равномерным, если на интервале, которому принадлежат все возможные значения случайной величины, дифференциальная функция имеет постоянное значение.
Случайные величины, имеющие равномерное распределение вероятностей, <<встречаются на практике. Например, при снятии показаний измерительных приборов. Ошибка при округлении отсчёта до ближайшего целого деления шкалы является случайной величиной, которая может с постоянной плотностью вероятности принимать любые значения между двумя соседними делениями. Таким образом, данная случайная величина имеет равномерное распределение.
Найдём дифференциальную функцию (плотность) равномерного распределения, считая, что все возможные значения случайной величины Х заключены в промежутке [a,b] , на котором дифференциальная функция сохраняет постоянное значение, то есть
f(x) = C
По условию Х не принимает значений вне промежутка [a,b] , поэтому f(x) = 0 при всех x < a и x < b.
Найдём значение постоянной С. Так как все возможные значения случайной величины принадлежат промежутку[a,b] , то справедливо:
.
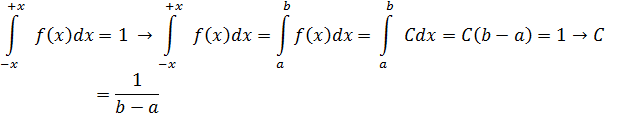
Итак, закон равномерного распределения случайной величины на отрезке[a,b] (здесь a < b ) аналитически можно записать так:

|
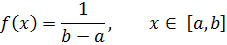
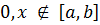
Найдём теперь интегральную функцию равномерного распределения непрерывной случайной величины. Для этого воспользуемся формулой
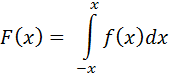
Тогда:
если x < a то f(x) = 0 и, следовательно, F(x) = 0
если a ≤ x ≤ b то 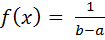 и, следовательно
и, следовательно
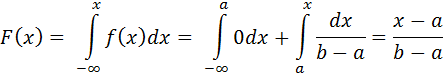
.
если x ˃ b то
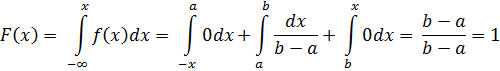
Итак, искомая интегральная функция распределения аналитически может быть записана так:

|
F(x) = 0 при x < a
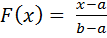 при a ≤ x ≤ b
при a ≤ x ≤ b
F(x) = 1 при x ˃ b
Свойства равномерного непрерывного распределения:
1. Первый момент (математическое ожидание)
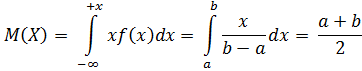
2. Медиана: M = M(X)
3. Мода – любое число на отрезке 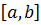 (мода – наиболее вероятное значение распределения);
(мода – наиболее вероятное значение распределения);
4. Дисперсия
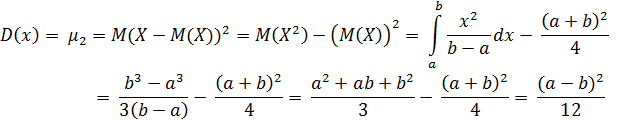
5. Среднее квадратическое отклонение
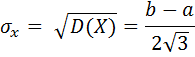
6. В силу симметрии распределения все нечётные моменты равны нулю.
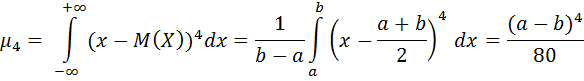
Тогда
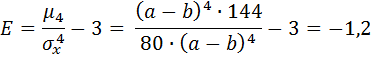
7.
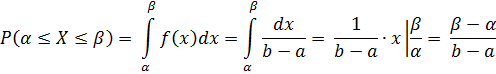
ПРИМЕР 2.Троллейбусы идут строго по расписанию и с интервалом в 6 мин. Найти вероятность того, что пассажир, подошедший к остановке, будет ожидать троллейбус менее двух минут.
Решение. Время ожидания троллейбуса есть непрерывная случайная величина Х, имеющая равномерное распределение на промежутке [0,6], так как с равной вероятностью время ожидания может быть любым в этом промежутке. Тогда
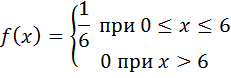
Тогда
. 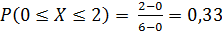
Треугольный закон распределения непрерывной случайной величины.
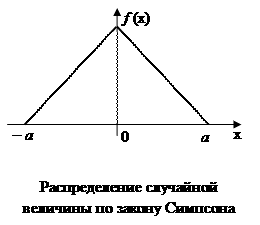
К распределению по закону Симпсона приводит сложение двух случайных величин, подчиненных закону равной вероятности при одинаковых параметрах рассеяния. Кривая рассеяния имеет вид равнобедренного треугольника, из-за чего закон Симпсона часто называют законом треугольника.
При выборе в качестве начала отсчета случайной величины ее плотность распределения и математическое ожидание имеют следующий вид:
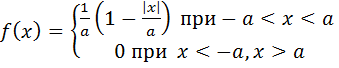
Mx = 0 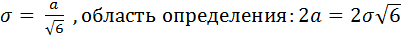
Дата добавления: 2016-06-15; просмотров: 20237;











