Минимизация методом Квайна – Мак-Класки
Метод Квайна – Мак-Класки отличается от метода Квайна большей формализацией. Это достигается путем использования кубического представления ПФ (см. п. 3.6 учебного пособия) и сокращения перебора при выполнении операции склеивания. С учетом большей формализации метод Квайна – Мак-Класки удобно использовать при машинной реализации алгоритмов минимизации ПФ. Рассмотрим основные этапы этого метода.
На первом этапе необходимо представить ПФ в виде кубического комплекса 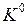 , представляющего собой совокупность 0-кубов, на которых минимизируемая ПФ принимает значение 1. Для этого в СДНФ функции каждый дизъюнктивный член заменяется n-разрядной двоичной комбинацией (n – число аргументов функции), представляющей собой номер конституенты 1, соответствующей этому дизъюнктивному члену. Иными словами, записываются n-разрядные двоичные наборы, на которых значение функции равно 1.
, представляющего собой совокупность 0-кубов, на которых минимизируемая ПФ принимает значение 1. Для этого в СДНФ функции каждый дизъюнктивный член заменяется n-разрядной двоичной комбинацией (n – число аргументов функции), представляющей собой номер конституенты 1, соответствующей этому дизъюнктивному члену. Иными словами, записываются n-разрядные двоичные наборы, на которых значение функции равно 1.
Далее все 0-кубы полученного кубического комплекса разбиваются на группы по числу единиц, входящих в их запись. Таким образом, максимальное число групп не превышает 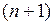 .
.
Производится склеивание 0-кубов, которое возможно только между соседними группами. Результаты склеивания составляют новый кубический комплекс 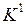 . Если часть 0-кубов не участвовала в склеивании, то такие 0-кубы являются простыми импликантами.
. Если часть 0-кубов не участвовала в склеивании, то такие 0-кубы являются простыми импликантами.
Формирование кубических комплексов продолжается до тех пор, пока не будет получен комплекс 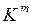 , не содержащий m-кубов, отличающихся только по одной координате. При этом сохраняется разбиение на группы по количеству единиц. Если на каком-либо этапе часть i-кубов не участвовала в склеивании, то такие i-кубы являются простыми импликантами и входят в минимальную ДНФ.
, не содержащий m-кубов, отличающихся только по одной координате. При этом сохраняется разбиение на группы по количеству единиц. Если на каком-либо этапе часть i-кубов не участвовала в склеивании, то такие i-кубы являются простыми импликантами и входят в минимальную ДНФ.
Рассмотрим пример.
Пусть подлежащая минимизации ПФ задана картой Карно (табл. 4.10).
Таблица 4.10

| x2 | ||||
    x1
x1
| |||||
| x3 | |||||

| |||||

| x4 |
Заранее отметим на ней возможные простые импликанты для проверки правильности решения примера.
Для рассматриваемой функции СДНФ запишется в следующем виде:
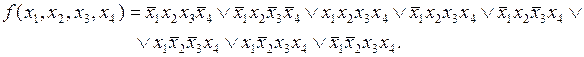
По СДНФ функции сформируем кубический комплекс 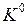 , каждый элемент которого представляет собой четырехразрядный двоичный набор. Если переменная
, каждый элемент которого представляет собой четырехразрядный двоичный набор. Если переменная 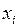 входит в запись конституенты 1 без инверсии, то i-й разряд двоичного набора, соответствующего этой конституенте 1, принимает значение 1. В противном случае i-й разряд двоичного набора, соответствующего этой конституенте 1, принимает значение 0.
входит в запись конституенты 1 без инверсии, то i-й разряд двоичного набора, соответствующего этой конституенте 1, принимает значение 1. В противном случае i-й разряд двоичного набора, соответствующего этой конституенте 1, принимает значение 0.
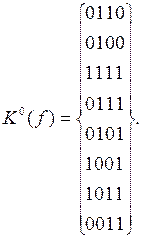
Сведем в таблицу (табл. 4.11) полученные 0-кубы, упорядоченные по числу единиц.
Таблица 4.11
| Кол-во единиц | 0-кубы |
| – | |
| 0110, 0101, 1001, 0011 | |
| 0111, 1011 | |
Произведем склеивание по одной переменной между элементами соседних групп. В результате будут получены элементы кубического комплекса 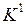 , которые также сведем в таблицу (табл. 4.12).
, которые также сведем в таблицу (табл. 4.12).
Таблица 4.12
| Кол-во единиц | 1-кубы |
| 01X0, 010X, | |
| 011X, 01X1, 10X1, 0X11, X011 | |
| X111, 1X11 |
Необходимо включать во все последующие таблицы 0-кубы и импликанты, не участвовавшие в склеивании, а затем исключать лишние по правилу поглощения.
Будем продолжать процедуру склеивания до тех пор, пока элементы очередного кубического комплекса могут склеиваться по одной переменной. При этом склеивание возможно только между i-кубами, имеющими одинаковые несущественные переменные (имеющими символ «Х» в одинаковых позициях).
Для рассматриваемого примера кубический комплекс 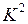 , сформированный путем склеивания элементов комплекса
, сформированный путем склеивания элементов комплекса 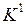 , представлен в табл. 4.13. Повторяющиеся 2-кубы исключены.
, представлен в табл. 4.13. Повторяющиеся 2-кубы исключены.
Таблица 4.13
| Кол-во единиц | 2-кубы |
 1 1
| 01ХХ, 01ХХ |
 2 2
| 10X1, ХХ11, ХХ11 |
Дальнейшее склеивание невозможно, поэтому кубический комплекс 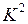 представляет собой совокупность простых импликант.
представляет собой совокупность простых импликант.
Составим импликантную матрицу Квайна (табл. 4.14) для нахождения минимальной совокупности простых импликант, представляющих в минимальной ДНФ все конституенты единицы исходной СДНФ. В рассматриваемом примере требуется найти минимальную совокупность 2-кубов, накрывающих все 0-кубы минимизируемой ПФ.
Таблица 4.14
| № | 0-кубы | 2-кубы | ||
| 01ХХ | 10X1 | ХХ11 | ||
| + | ||||
| + | ||||
| + | ||||
| + | ||||
| + | ||||
| + | + | |||
| + | + | |||
| + |
Из полученной импликантной матрицы видно, что все найденные на предыдущем этапе минимизации 2-кубы входят в минимальную совокупность простых импликант, т.е. все элементы кубического комплекса 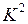 образуют минимальную ДНФ заданной ПФ.
образуют минимальную ДНФ заданной ПФ.
Окончательно,
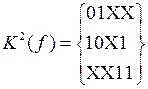 ,
,
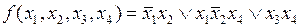 .
.
Полученное решение нетрудно проверить с помощью карты Карно (см. табл. 4.10).
Дата добавления: 2020-02-05; просмотров: 1097;











