Минимизация ПФ методом Блейка – Порецкого
Применение метода Квайна и метода Квайна –Мак-Класки для минимизации булевых функций требует преобразования произвольной ДНФ минимизируемой функции к СДНФ. В общем случае для осуществления такого преобразования можно пользоваться следующим соотношением: 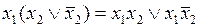 . Таким образом, для преобразования дизъюнктивного члена некоторой произвольной ДНФ необходимо выполнить умножение этого дизъюнктивного члена на дизъюнкцию прямого и инверсного значений отсутствующей переменной. В качестве примера можно привести следующее преобразование:
. Таким образом, для преобразования дизъюнктивного члена некоторой произвольной ДНФ необходимо выполнить умножение этого дизъюнктивного члена на дизъюнкцию прямого и инверсного значений отсутствующей переменной. В качестве примера можно привести следующее преобразование:
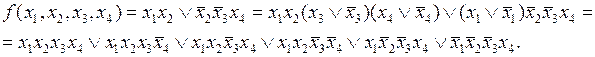
Как видно из этого условного примера, преобразование произвольной ДНФ к СДНФ требует довольно громоздких вычислений даже для функции четырех аргументов. Для функций большего числа аргументов процесс преобразования еще больше усложняется. Поэтому для минимизации функций, заданных произвольными ДНФ, удобно применять метод Блейка – Порецкого, не требующий задания ПФ в виде СДНФ.
Докажем справедливость следующего равенства, которое называется формулой обобщенного склеивания:
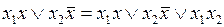 .
.
Равенство легко доказывается путем выполнения преобразований над его правой или левой частью. Преобразуем правую часть равенства.
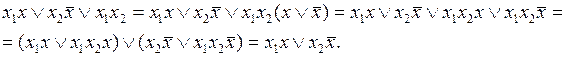
Поскольку в результате преобразований из правой части формулы обобщенного склеивания получена левая часть, то равенство доказано.
Метод Блейка – Порецкого основывается на утверждении: если в произвольной ДНФ минимизируемой ПФ произвести все возможные обобщенные склеивания и все возможные поглощения, то в результате будет получена сокращенная ДНФ исходной функции.
Для получения минимальной ДНФ необходимо составить импликантную матрицу Квайна и определить по ней минимальное покрытие единиц минимизируемой функции простыми импликантами.
Рассмотрим пример. Пусть подлежащая минимизации функция задана в следующем виде:
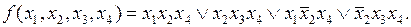
На первом этапе минимизации проведем всевозможные обобщенные склеивания.
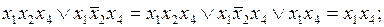
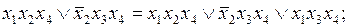
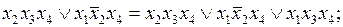
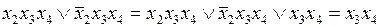 .
.
Исключив повторения элементарных произведений, получим ДНФ:
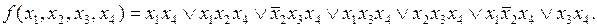
Выполнив все возможные поглощения, получим сокращенную ДНФ:
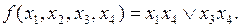
Построив импликантную матрицу (табл. 4.15), легко убедиться, что полученная сокращенная ДНФ является минимальной.
Таблица 4.15
| № | Исходные слагаемые | Простые импликанты | |
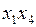
| 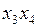
| ||
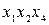
| + | ||
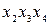
| + | ||
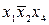
| + | ||
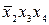
| + |
4.5. Минимизация ПФ,
заданных в конъюнктивной форме
Для минимизации ПФ, заданных в виде КНФ, можно использовать все вышеизложенные методы с незначительными отличиями. Отличия заключаются в записи соотношений склеивания и поглощения в конъюнктивной форме, а также в использовании некоторых понятий, характерных для КНФ.
Конституентой 0 называется функция, принимающая значение 0 на одном наборе значений аргументов. В конъюнктивной форме конституента 0 записывается как элементарная дизъюнкция всех переменных, причем переменная входит в дизъюнкцию с отрицанием, если ей соответствует цифра 1 в наборе. Например, конституента 0 ( 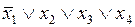 ) принимает значение 0 на наборе (1000).
) принимает значение 0 на наборе (1000).
Понятие импликанты и простой импликанты заменяется для КНФ на понятие имплиценты и простой имплиценты.
Имплицентой функции f называется функция, принимающая значение 0 на тех же наборах (или на части тех же наборов), на которых функция f принимает нулевое значение.
Простой имплицентой функции f называется имплицента, никакая часть которой не является сама по себе имплицентой f.
Для минимизации ПФ, заданной КНФ, как и в методах минимизации ДНФ, необходимо выполнить два этапа. На первом этапе осуществляется нахождение сокращенной КНФ, т.е. конъюнкции всех простых имплицент. При этом можно пользоваться соотношениями склеивания и поглощения, адаптированными для КНФ. Формула склеивания записывается как
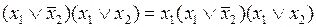 ,
,
а формула обобщенного склеивания как
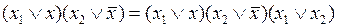 .
.
После нахождения всех возможных склеиваний следует выполнить все возможные поглощения по формуле
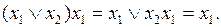
Для получения минимальной КНФ по сокращенной КНФ следует сформировать имплицентную матрицу Квайна, по которой определяется минимальное покрытие простыми имплицентами всех конституент 0 минимизируемой функции.
При минимизации ПФ с помощью карт Карно главное отличие заключается в поиске совокупностей, состоящих из 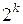 нулей. Все остальное можно оставить без изменений, но при этом в записи минимальной КНФ значения переменных следует инвертировать. Например, пусть подлежащая минимизации ПФ задана в виде карты Карно (табл. 4.16).
нулей. Все остальное можно оставить без изменений, но при этом в записи минимальной КНФ значения переменных следует инвертировать. Например, пусть подлежащая минимизации ПФ задана в виде карты Карно (табл. 4.16).
Таблица 4.16

| x2 | ||||
    x1
x1
| |||||
| x3 | |||||

| |||||

| x4 |
Тогда ее минимальная КНФ запишется в следующем виде:
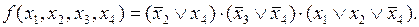
В общем случае до решения задачи минимизации ПФ нельзя сказать, какая из минимальных форм (ДНФ или КНФ) окажется проще. В некоторых случаях удобно использовать для получения минимальной ДНФ минимизацию по нулям. При этом будет получена минимальная ДНФ для функции 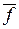 .
.
Дата добавления: 2020-02-05; просмотров: 1110;











