Минимизация ПФ с помощью карт Карно
Карта Карно (диаграмма Вейча) для функции 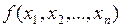 представляет собой прямоугольную таблицу, состоящую из 2n клеток, где каждой строке (столбцу) или группе строк (столбцов) соответствует прямое или инверсное значение одной из переменных. Каждой клетке такой таблицы ставится в соответствие набор аргументов функции. В клетке карты Карно записывается единица, если функция
представляет собой прямоугольную таблицу, состоящую из 2n клеток, где каждой строке (столбцу) или группе строк (столбцов) соответствует прямое или инверсное значение одной из переменных. Каждой клетке такой таблицы ставится в соответствие набор аргументов функции. В клетке карты Карно записывается единица, если функция 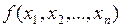 на соответствующем этой клетке наборе принимает значение 1, в противном случае в соответствующую клетку записывается 0. Таким образом, карта Карно является разновидностью таблицы истинности булевой функции.
на соответствующем этой клетке наборе принимает значение 1, в противном случае в соответствующую клетку записывается 0. Таким образом, карта Карно является разновидностью таблицы истинности булевой функции.
В табл. 4.2–4.5 приведены карты Карно в общем виде для функций двух, трех, четырех и пяти аргументов. В ячейках этих карт Карно записаны соответствующие им наборы аргументов.
Таблица 4.2

| 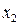
| |
 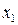
| 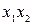
| 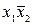
|
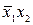
| 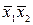
|
Таблица 4.3

| 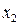
| |||
 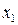
| 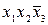
| 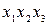
| 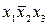
| 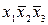
|
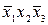
| 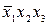
| 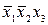
| 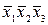
| |

| 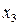
|
Таблица 4.4

| 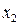
| ||||
 
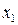
| 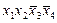
| 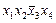
| 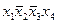
| 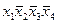
| |
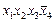
| 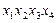
| 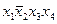
| 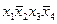
|
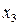
| |
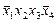
| 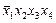
| 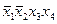
| 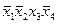
| ||
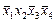
| 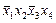
| 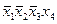
| 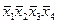
| ||

| 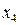
|
Таблица 4.5

| 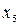
| ||||||||

| 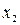
| ||||||||

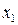
| |||||||||

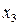
| |||||||||

| 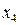
| 
| 
|
Карты Карно для функций большего числа аргументов строятся аналогичным образом. При этом в любой карте Карно соседние наборы, отличающиеся значением только одной переменной, находятся в соседних клетках. Крайние столбцы и строки карты Карно также содержат соседние наборы.
Метод минимизации ПФ с помощью карт Карно основан на так называемой операции полного склеивания: 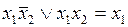 . При этом говорят, что два дизъюнктивных члена склеиваются по переменной
. При этом говорят, что два дизъюнктивных члена склеиваются по переменной 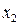 . Таким образом, соседние наборы склеиваются по одной из переменных.
. Таким образом, соседние наборы склеиваются по одной из переменных.
Общее правило склеивания на картах Карно можно сформулировать следующим образом: склеиванию подлежат совокупности соседних ячеек, содержащих одинаковые значения заданной ПФ, общее число которых кратно 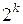 ,
, 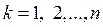 . Результатом такого склеивания является элементарное произведение переменных, значения которых не изменялись на всех склеиваемых наборах.
. Результатом такого склеивания является элементарное произведение переменных, значения которых не изменялись на всех склеиваемых наборах.
Для получения минимальной ДНФ по карте Карно необходимо выполнить следующие действия.
1. Определить совокупности 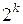 соседних ячеек с единичным значением функции. Необходимо стремиться объединить в одну совокупность как можно большее количество соседних ячеек карты, а общее число совокупностей должно быть минимальным. При этом некоторые единицы уже выделенных совокупностей могут участвовать в формировании других совокупностей соседних ячеек.
соседних ячеек с единичным значением функции. Необходимо стремиться объединить в одну совокупность как можно большее количество соседних ячеек карты, а общее число совокупностей должно быть минимальным. При этом некоторые единицы уже выделенных совокупностей могут участвовать в формировании других совокупностей соседних ячеек.
2. Определить элементарные произведения, получающиеся путем склеивания соседних ячеек, определенных на предыдущем шаге.
3. Записать минимальную ДНФ функции как дизъюнкцию полученных элементарных конъюнкций.
Рассмотрим несколько примеров минимизации по картам Карно.
Пример 1. Минимизировать с помощью карты Карно ПФ, заданную следующим выражением:
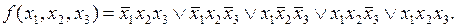
Карта Карно для этой функции имеет вид, представленный в табл. 4.6.
Таблица 4.6

| x2 | |||
    x1 x1
| ||||

| x3 |
Прямоугольниками обозначены совокупности соседних 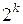 ячеек, выделяемых для операции склеивания. Единица в ячейке
ячеек, выделяемых для операции склеивания. Единица в ячейке 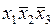 (крайний правый столбец) может объединяться с единицей
(крайний правый столбец) может объединяться с единицей 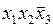 , поскольку эти две ячейки являются соседними.
, поскольку эти две ячейки являются соседними.
Для определения результатов склеивания достаточно записать элементарные произведения переменных, которые накрывают выделенные совокупности ячеек. Из табл. 4.5 следует, что совокупность из четырех единиц (наборы 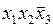 ,
, 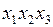 ,
, 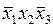 ,
, 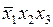 ) может быть накрыта только переменной
) может быть накрыта только переменной 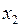 , а остальные две переменные накрывают только часть этой совокупности, поэтому первым элементарным произведением будет
, а остальные две переменные накрывают только часть этой совокупности, поэтому первым элементарным произведением будет 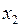 . Вторая выделенная совокупность соседних ячеек (наборы
. Вторая выделенная совокупность соседних ячеек (наборы 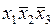 ,
, 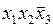 ) может быть накрыта элементарным произведением
) может быть накрыта элементарным произведением 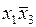 , поскольку эти две ячейки расположены в строке, отмеченной переменной
, поскольку эти две ячейки расположены в строке, отмеченной переменной 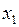 , и столбцы, соответствующие этой совокупности ячеек, отмечены инверсным значением переменной
, и столбцы, соответствующие этой совокупности ячеек, отмечены инверсным значением переменной 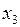 .
.
Таким образом, минимальная ДНФ для заданной функции имеет вид
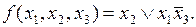
Рассмотрим еще несколько примеров получения минимальной ДНФ по карте Карно. При этом будем задавать исходные ПФ в виде карт Карно, так как процедура перехода от СДНФ к карте и наоборот выполняется элементарно. Также для простоты будем записывать в ячейки только единичные значения функции, а ячейки с нулевыми значениями будем оставлять незаполненными.
Пусть минимизируемая функция задана картой Карно (табл. 4.7).
Таблица 4.7
     
| x2 | ||||
 x1
x1
| |||||
| x3 | |||||

| |||||

| x4 |
Поскольку минимальное число совокупностей соседних ячеек, объединяющих все единицы исходной функции, равно трем, минимальная ДНФ для функции, заданной табл. 4.6, включает в себя три слагаемых:
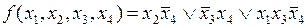 .
.
Пусть минимизируемая функция задана картой Карно (табл. 4.8).
Таблица 4.8

| x2 | ||||
     x1
x1
| |||||
| x3 | |||||

| |||||

| x4 |
Поскольку единица в ячейке 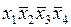 не имеет подходящих для склеивания соседей, она входит в минимальную ДНФ в виде элементарного произведения всех четырех аргументов:
не имеет подходящих для склеивания соседей, она входит в минимальную ДНФ в виде элементарного произведения всех четырех аргументов:
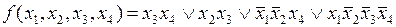 .
.
Дата добавления: 2020-02-05; просмотров: 754;











