Минимизация ПФ методом Квайна

Идея минимизации ПФ методом Квайна заключается в применении двух соотношений:

1) 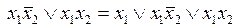– соотношение (неполного) склеивания;

2) 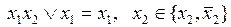– соотношение поглощения.

Справедливость этих соотношений можно проверить при помощи элементарных преобразований или по таблицам истинности.

Теорема Квайна. Если в совершенной дизъюнктивной нормальной форме ПФ провести все операции неполного склеивания и затем все операции поглощения, то в результате получится сокращенная ДНФ исходной ПФ, т.е. дизъюнкция всех ее простых импликант.

Доказательство этой теоремы приводится, например, в [7], при этом используется операция развертывания, обратная операции склеивания:

.

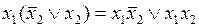Из формулировки теоремы Квайна следует, что в качестве исходной формы представления ПФ должна использоваться СДНФ. Если функция задана в произвольной форме, то вначале ее следует преобразовать к СДНФ. При этом переход от произвольной ДНФ к СДНФ осуществляется путем применения операции развертывания.

Практическое применение метода Квайна можно условно разделить на два этапа. На первом этапе минимизации производятся все возможные склеивания и поглощения по заданной СДНФ минимизируемой функции. В результате получается сокращенная ДНФ.

На втором этапе для получения минимальной ДНФ необходимо исключить из сокращенной ДНФ все лишние простые импликанты. Это делается с помощью так называемой импликантной матрицы Квайна, которая представляет собой таблицу, столбцы которой отмечаются простыми импликантами, т.е. дизъюнктивными членами полученной на предыдущем этапе сокращенной ДНФ, а строки – членами СДНФ минимизируемой ПФ. При этом в ячейке импликантной матрицы на пересечении i-й строки и j-го столбца ставится отметка, если соответствующая этому столбцу импликанта является частью члена СДНФ, которому соответствует j-я строка.

Минимальная ДНФ строится по импликантной матрице следующим образом. Анализируются все возможные совокупности простых импликант (столбцы матрицы), накрывающие все члены СДНФ (строки матрицы). Простая импликанта накрывает член СДНФ, если на пересечении соответствующей строки и столбца матрицы имеется отметка. Одна импликанта может накрывать несколько строк. Из этих совокупностей выбирается одна (или несколько) с наименьшим числом членов (простых импликант), которая определяет минимальную ДНФ.

Для сокращения перебора можно пользоваться следующим подходом. Вначале по возможности определяются строки импликантной матрицы, в которых имеется только одна отметка. Простые импликанты, которым соответствуют эти отметки, называются базисными и обязательно входят в минимальную ДНФ функции, так как только эти простые импликанты в минимальной ДНФ представляют члены исходной СДНФ, записанные в найденных строках. Остальные строки импликантной матрицы должны быть накрыты минимальным числом простых импликант. В некоторых случаях базисные импликанты могут накрывать все строки.

Рассмотрим пример.

Пусть ПФ задана картой Карно (табл. 4.6). Ее СДНФ имеет вид

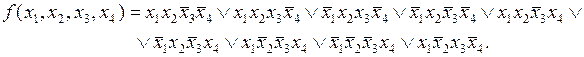
На первом этапе выполним все склеивания конституент 1 по одной переменной. При этом будет получена совокупность элементарных произведений, являющихся импликантами и представляющих собой общие части склеиваемых конституент. Для удобства присвоим каждому получаемому элементарному произведению порядковый номер. Не участвовавшие в очередном склеивании конституенты 1 или импликанты должны входить в последующие совокупности импликант в неизмененном виде.

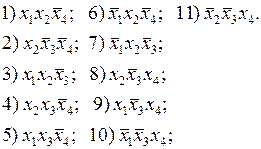
Повторим процедуру склеивания по одной переменной над каждой парой элементов совокупности импликант, полученных на предыдущем шаге. Будем повторять эту процедуру до тех пор, пока остаются элементарные произведения, между которыми возможно склеивание. Каждому элементу новой совокупности поставим в соответствие индекс, составленный из индексов импликант, участвующих в склеивании.

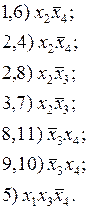
Полученную совокупность необходимо дополнить определенной на предыдущем этапе импликантой с порядковым номером 5, так как эта импликанта не участвовала в последующем склеивании (является простой).

Над полученной совокупностью элементарных произведений необходимо выполнить процедуру поглощения. В рассматриваемом примере совокупность элементарных произведений не содержит элементов, способных поглощать другие элементы, за исключением повторяющихся.

Окончательно, после исключения повторяющихся элементов, совокупность импликант запишется в следующем виде:

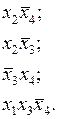
Дальнейшее выполнение склеиваний и поглощений невозможно.

Запишем сокращенную ДНФ минимизируемой функции:

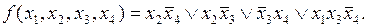
Построим импликантную матрицу Квайна (табл. 4.9).

Таблица 4.9

№	Конституенты 1	Простые импликанты
		+	+
		+			+
		+
		+	+
			+	+
			+	+
				+
				+
					+

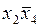
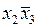
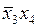
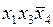
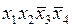
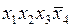
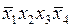
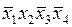
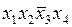
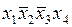
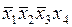
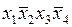
Поставим отметки в ячейках импликантной матрицы, находящихся на пересечении таких строк и столбцов, в которых простая импликанта является частью соответствующей конституенты 1.

Отыщем минимальное покрытие столбцами всех строк таблицы. Столбец импликантной матрицы, которому соответствует простая импликанта 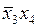, обязательно должен войти в минимальное покрытие, поскольку только эта импликанта накрывает строки 7 и 8 матрицы.

Кроме того, простая импликанта 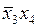может представлять в минимальной совокупности еще две конституенты 1, находящиеся в строках 5 и 6.

Аналогичные рассуждения можно провести в отношении простой импликанты 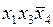, поскольку только она может представлять в минимальной совокупности простых импликант строку 9 импликантной матрицы. Отметим, что эта импликанта также накрывает конституенту 1, записанную в строке 2.

Таким образом, задача упростилась и заключается в нахождении минимального покрытия оставшихся трех конституент 1 (строки 1, 3, 4) оставшимися простыми импликантами.

Очевидно, что простая импликанта 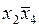накрывает оставшиеся три строки матрицы. Следовательно, простая импликанта 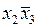оказалась лишней и в минимальную ДНФ не входит.

Окончательно минимальная ДНФ запишется в виде

.

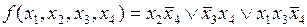Метод Квайна является базовым методом минимизации ПФ.