Риски сбоя в комбинационных схемах

Рассмотрим работу КС, изображенной на рис. 3.7, реализующей функцию .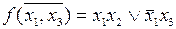

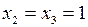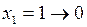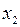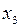Пусть на входах схемы последовательно формируются следующие сигналы: , , т.е. сигналы на входах и остаются неизменными, а сигнал на входе 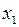изменяется из 1 в 0. Логические элементы схемы вносят различные задержки в процесс распространения сигналов. На рис. 3.8 приведены временные диаграммы для возможного изменения сигналов в рассматриваемой схеме.

Несмотря на то, что для рассматриваемой функции и реализующей ее схемы 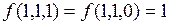, в течение некоторого времени на выходе схемы может быть сформирован уровень логического нуля, являющийся в данном случае ложным сигналом. Появление ложных сигналов на выходах схемы называется риском сбоя. Риски сбоя являются следствием конечной скорости распространения сигналов и ненулевых задержек логических элементов.

Различают статические и динамические риски сбоя. При статических рисках сбоя во время переходного процесса значение на выходе схемы изменяется четное число раз. При динамических рисках сбоя, являющихся следствием статических, – нечетное число раз.

Риски сбоя в схемах могут вызывать ложные срабатывания управляемых устройств, для которых сигналы КС являются входными.

С целью исключения рисков сбоя в схемах, для которых в любой момент времени может изменяться значение только одного входного сигнала, необходимо выполнять их синтез таким образом, чтобы любые пары единиц функции, которым соответствуют конституенты 1, отличающиеся по одной переменной, были представлены произведением в ДНФ. Для этих целей удобно использовать таблично-графическое представление ПФ, называемое картой Карно (диаграммой Вейча). Карты Карно подробно рассмотрены в разделе 4.1 учебного пособия.

Приведем карту Карно для рассматриваемой функции (табл. 3.12).

Таблица 3.12

	x2
x1	1	1
	1
		x3

Таким образом, действуя по приведенному выше правилу, для исключения рисков сбоя в схеме, реализующей данную функцию, необходимо ввести в ДНФ функции конъюнкцию 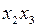, а в КС – соответствующий этому произведению дополнительный логический элемент.

Рассмотрим еще один способ устранения рисков сбоя для ситуации, когда изменяются более одного входного сигнала. В этом случае ячейки карты Карно, соответствующие реализуемым единичным сигналам функции, не будут являться соседними.

Пусть реализуемая функция имеет вид 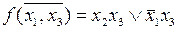. Соответствующая карта Карно представлена на рис. 3.9. Предположим, что в процессе работы схемы на ее входах последовательно появляются наборы (1,1,1) и (0,0,1).

Поскольку абсолютно одновременное изменение сигналов на входе КС невозможно, переход от единицы функции, реализуемой на первом из рассматриваемых наборов входных сигналов, к единице, соответствующей второму набору, может быть выполнен одним из двух способов.

	x2
x1		1
		x3

Рис. 3.9

В первом случае, если входной сигнал 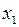изменится быстрее 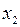, произойдет переход 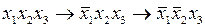и на выходе схемы единичный сигнал не изменится. В другом случае сигнал 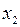изменится быстрее 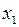и произойдет переход 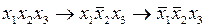. Поскольку 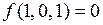, в данной ситуации может возникнуть изменение выходного сигнала вида 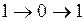, указывающее наличие в схеме риска сбоя. Рассмотренное явление носит название функционального риска сбоя.

В некоторых случаях подобные риски сбоя могут быть устранены. Если, например, в рассматриваемом примере работа схемы организована таким образом, что после входного набора (1, 1, 1) следует набор (0, 0, 1) и отсутствует обратная последовательность, то введение достаточной задержки в процесс изменения сигнала 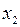относительно изменения 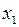может обеспечить требуемый безопасный вариант переключения схемы.

Вопросы для самоконтроля

1. Каково максимальное число ПФ, зависящих от n переменных?

2. Какие способы задания ПФ вам известны?

3. Какие элементарные логические функции вам известны и для чего они используются?

4. Каким условиям должен удовлетворять набор логических функций, образующий функционально полную систему (базис)?

5. Какие канонические формы аналитического представления ПФ вам известны и как они формируются?

6. Что представляют собой дешифраторы и мультиплексоры и как с их помощью могут быть реализованы переключательные функции?

7. Что понимают под рисками сбоя и каковы причины их появления?

4. МИНИМИЗАЦИЯ
ПЕРЕКЛЮЧАТЕЛЬНЫХ ФУНКЦИЙ

Рассмотрим СДНФ некоторой функции 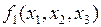и выполним ряд элементарных преобразований, воспользовавшись соотношениями, приведенными в разделе 3.3.

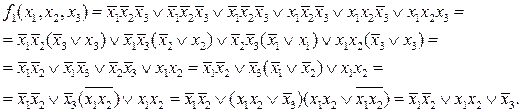
Справедливость полученного равенства можно проверить, сравнив, например, таблицы истинности для исходной и конечной записи ПФ.

Для технической реализации функции 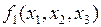по исходной СДНФ в каноническом базисе И-ИЛИ-НЕ необходимо использовать шесть трехвходовых элементов «И», реализующих конъюнкции переменных, три элемента «НЕ», реализующих инверсии переменных, и один шестивходовый элемент «ИЛИ», реализующий дизъюнкцию всех заданных конъюнкций входных переменных. Для реализации той же ПФ по аналитической записи, полученной после выполнения преобразований, потребуются два двухвходовых элемента «И», три инвертора и один трехвходовый элемент «ИЛИ».

Таким образом, если принять за единицу цены схемы один логический элемент, используемый при технической реализации, и один вход логического элемента, то можно дать оценку сложности технической реализации КС путем суммирования количества необходимых для синтеза схемы логических элементов и количества их входов. Возможны и другие методы оценки стоимости технической реализации КС.

Для рассмотренной ПФ цена схемы, синтезируемой по СДНФ, составляет (без учета инверторов): С₁ = 6+(6∙3)+1+6 = 31. Цена схемы, синтезируемой по упрощенной форме представления ПФ, составляет (также без учета инверторов): С₂ = 2+(2∙2)+1+3 = 10.

Задача минимизации ПФ заключается в отыскании минимальных форм представления функций, поскольку им соответствуют наиболее простые технические реализации (с наименьшей ценой схемы). Иными словами, при решении задачи минимизации ПФ требуется найти аналитическое выражение заданной ПФ или системы ПФ, содержащее наименьшее число переменных и логических функций. Решение этой задачи в общем случае затруднено. Наиболее подробно исследовано решение задачи минимизации для канонического базиса И-ИЛИ-НЕ. Также известны подходы к решению этой задачи для ПФ, заданных в базисах И-НЕ, ИЛИ-НЕ.

Введем ряд определений.

Элементарной конъюнкцией называется конъюнкция конечного числа различных переменных, входящих в нее в прямом или инверсном значении.

Дизъюнктивной нормальной формой (ДНФ) называется дизъюнкция элементарных конъюнкций.

ДНФ переключательной функции называется минимальной, если она содержит наименьшее число букв по отношению к любой другой ДНФ той же функции. Следует различать буквы и переменные. Например, ДНФ 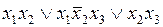содержит семь букв.

Если некоторая булева функция g принимает значение 0 на тех же наборах, на которых принимает значение 0 другая булева функция f , то функция g называется импликантой функции f. Это определение можно также сформулировать в другом виде. Функция g называется импликантой функции f, если для любого набора переменных, на котором 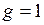, функция f также принимает значение 1.

Простой импликантой переключательной функции f называется импликанта g, если никакие отдельные части этой импликанты не являются сами по себе импликантами f.

Проиллюстрируем последние два определения примером. В табл. 4.1 заданы функция f и ее импликанты g₁, g₂, …, g₇.

Таблица 4.1

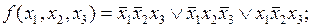
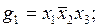
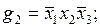
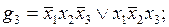
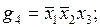
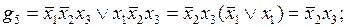
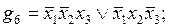
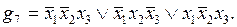
Из приведенных определений следует, что импликанты g₂ и g₅ являются простыми, а, например, импликанта g₄ не является простой, так как ее часть 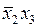также является импликантой функции f.

Из определения импликанты следует, что дизъюнкция любого числа импликант функции f также является импликантой этой функции.

Сокращенной ДНФ называется форма представления переключательной функции f, записываемая в виде дизъюнкции всех простых импли­- кант f.

Для ПФ из рассмотренного выше примера сокращенная ДНФ запишется следующим образом:

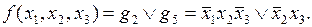
В некоторых случаях из сокращенной ДНФ можно исключить одну или несколько простых импликант таким образом, чтобы полученная функция была эквивалентна исходной. Такие простые импликанты называются лишними.

Сокращенная ДНФ булевой функции называется тупиковой (ТДНФ), если из нее не удается исключить лишние простые импликанты. Произвольная ПФ может иметь несколько ТДНФ.

Тупиковые ДНФ логической функции, содержащие минимальное число букв, являются минимальными. Произвольная ПФ может иметь несколько минимальных ДНФ.

Процесс отыскания минимальных ДНФ состоит из двух этапов: нахождения простых импликант и исключения лишних импликант.