Интерполирование функций
Основные вопросы, рассматриваемые на лекции:
1. Основные понятия интерполяции, задача, приводящая к приближению функции, геометрический смысл интерполирования
2. Интерполяционный многочлен Лагранжа
3. Схема Эйткена
4. Оценка погрешности интерполяционной формулы Лагранжа
5. Конечные разности
6. Интерполяционные формулы Ньютона
§ Первая интерполяционная формула Ньютона
§ Вторая интерполяционная формула Ньютона
7. Оценка погрешностей первой и второй интерполяционных формул Ньютона
8. Обратное интерполирование
9. Интерполяция сплайнами
- Основные понятия интерполяции, задача, приводящая к приближению функции
Интерполяция (от лат. interpolation - изменение, переделка) - в математике и статистике, отыскание промежуточных значений величины по некоторым известным её значениям [Сов. энциклопедический словарь].
Задача, приводящая к приближению функции, заключается в следующем. Известны значения функции f (x) в точках x1, x2, :, xn; требуется восстановить её значения при других х.
Интерполяционный полином, передающий свойства функции f (x) будем строить в виде:
Pn(x) = c1φ1(x) + c2φ2(x) + : + cnφn(x), где φ1(x), φ2(x), :, φn(x) - класс линейно-независимых функций, при этом Pn(xi) = f (xi), i = 1, 2, :, n.
Таким образом, Pn(x)  f(x).
f(x).
Точки x1, x2, :, xn называются узлами интерполяции.
· Интерполяционный многочлен Лагранжа
Пусть известны значения функции f (x) в (n+1) точке x0, x1, :, xn. Тогда многочлен Лагранжа, передающий свойства функции f (x), можно записать так:
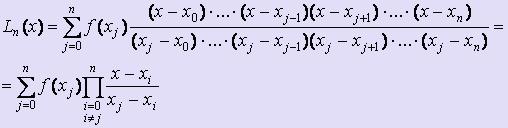
· Схема Эйткена
Схема Эйткена предлагает более удобную форму нахождения полинома Лагранжа.
Основная идея данного метода заключается в следующем.
На первом этапе вычисляются многочлены L0,1(x), L1,2(x), :, Ln-1,n(x), построенные на каждой паре соседних узлов 0,1; 1,2; :; n-1,n соответственно.
При этом 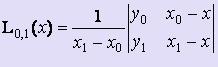 ,
, 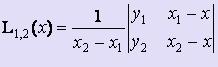 , :,
, :, 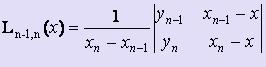 .
.
Таким образом, многочлены, построенные на паре соседних узлов, вычисляются по формулам: 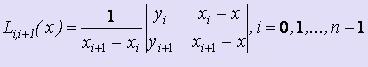 .
.
Затем на основе этих многочленов вычисляются многочлены, построенные на тройках соседних узлов: 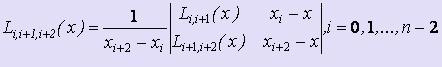 .
.
И т.д. пока не получится один многочлен, построенный на всех узлах интерполяции: 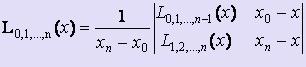 .
.
Полученный многочлен L0, 1, ..., n(x) 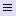 Ln(x).
Ln(x).
· Оценка погрешности интерполяционной формулы Лагранжа
Имеем yj = f ( xj ), Ln(x). Многочлен Ln(x) построен так, что Ln( xj ) = f ( xj ).
Вычисляя погрешность Rn(x) таким образом: Rn(x) = f (x) - Ln(x), можно получить следующую формулу для оценки погрешности интерполяционной формулы Лагранжа: 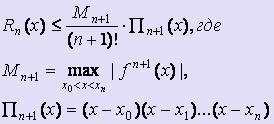 .
.
Такая оценка возможна только в том случае, когда известно аналитическое выражение для f. Если же f задана таблично, то производные заменяются конечными разностями.
· Интерполяционные формулы Ньютона
- Первая интерполяционная формула Ньютона
Пусть yi = f ( xi ), xi = x0 + ih, i = 1, 2, :, n.
Нужно построить Pn(x), удовлетворяющий двум условиям:
1. Степень полинома не должна превышать n.
2. Pn( xi ) = yi.
Формула Pn(x) для первой интерполяционной формулы Ньютона имеет вид: 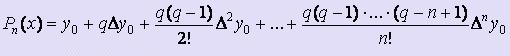 ,
,
где q = ( x - x0 ) / h.
Первая интерполяционная формула Ньютона применяется тогда, когда x находится вначале таблицы. Тогда в качестве x0 следует брать ближайшее слева к заданному x табличное значение.
- Вторая интерполяционная формула Ньютона
Когда значение аргумента находится ближе к концу отрезка интерполяции, применять первую интерполяционную формулу становится невыгодно.
Для этого применяется вторая интерполяционная формула Ньютона: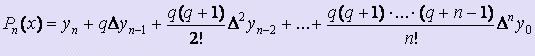 ,
,
где q = ( x - xn ) / h.
Здесь в качестве xn следует брать ближайшее справа к заданному x табличное значение.
· Оценка погрешностей первой и второй интерполяционных формул Ньютона
Используя подстановки q = ( x - x0 ) / h и q = ( x - xn ) / h и заменяя соответствующим образом выражение для Пn+1(x) в формуле оценки погрешности интерполяционной формулы Лагранжа, получим формулы для оценки погрешности интерполирования по первой и второй интерполяционной формуле Ньютона соответственно:
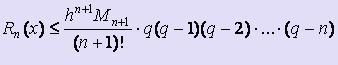 ,
,
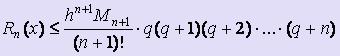 .
.
· Обратное интерполирование
Задача обратного интерполирования заключается в следующем. Если значения {yi} в таблице упорядочены по возрастанию или убыванию, то функция y = f (x) монотонна на [ x0 , xn ], и эту же таблицу можно интерпретировать как задание дискретного образа функции x = φ(y), обратной по отношению к функции y = f(x). Для этой обратной функции также может быть поставлена задача интерполирования: найти значение x* по заданному значению y*.
Пусть {xi} равноотстоящие узлы, расположенные на расстоянии h друг от друга и построен один из полиномов Ньютона (для определённости - первый): 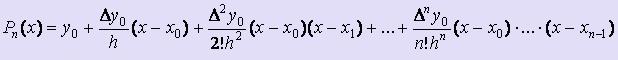 .
.
При решении задачи обратного интерполирования с помощью этого полинома в его левой части возникает известное значение y*, а сама формула становится алгебраическим уравнением относительно х. Если числа {yi} упорядочены по возрастанию или убыванию, то это уравнение имеет единственное решение на [ x0 , xn ].
Его решение следует искать любым из изученных ранее методов для решения нелинейных уравнений.
В рассматриваемом нами случае наиболее естественным способом для решения уравнения является метод простой итерации.
Подставим y = y* в вышепредставленную формулу и преобразуем получившееся равенство к виду: 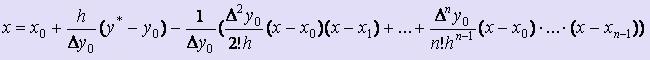 .
.
Это уравнение имеет структуру x = φ(x), т.е. по виду пригодно для применения метода простой итерации.
В качестве начального приближения можно взять значение x(0) = xi, ближайшее к искомому х*. Имея начальное приближение x(0), строим итерационный процесс для решения полученного уравнения пока не будет достигнута заданная точность: 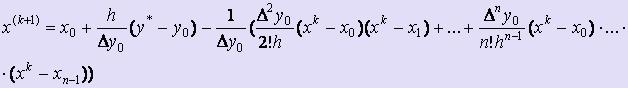
· Интерполяция сплайнами
При большом количестве узлов интерполяции сильно возрастает степень интерполяционных многочленов, что делает их неудобными для вычислений.
В этом случае удобно пользоваться особым видом кусочно-полиномиальной интерполяции - интерполяции сплайнами.
Суть этого подхода заключается в следующем.
Определение. Пусть отрезок [a, b] разбит точками на n частичных отрезков [xi , xi+1],i = 0, 1, :, n-1. Сплайном порядка m называется функция Sm (x), обладающая следующими свойствами:
1) Функция Sm (x) непрерывна на отрезке [a, b] вместе со своими производными до некоторого порядка р.
2) На каждом отрезке [xi , xi+1] функция совпадает с некоторым алгебраическим многочленомPm,i (x) степени m.
Разность m - p между степенью сплайна и наивысшим порядком непрерывной на отрезке [a, b] производной называют дефектом сплайна.
Будем рассматривать сплайны, дефект которых равен 1.
Наиболее широкое распространение получили кубические сплайны S3 (x).
Итак, для осуществления интерполяции необходимо построить такой сплайн, что S(xi ) = yi, i = 0, 1, :, n.
Согласно определению кубический сплайн можно представить в виде: 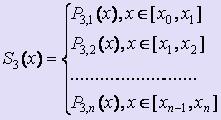 ,
,
где каждый из P3, i (x) - многочлен третьей степени: 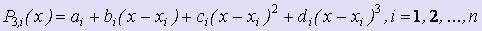 .
.
При этом коэффициенты ai = yi.
Можно показать, что коэффициенты сi вычисляются по формулам: 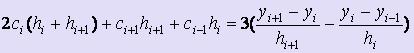 .
.
Для вычисления коэффициентов di используются формулы: 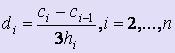 .
.
Для вычисления коэффициентов bi - формулы: 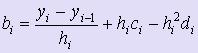 .
.
Дата добавления: 2017-05-02; просмотров: 7828;











