Решение однородных систем методом Гаусса
Однородная система 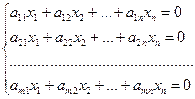 всегда совместна, так как она всегда имеет нулевое решение x1 = x2 = … = xn = 0. Для нее справедливо, что
всегда совместна, так как она всегда имеет нулевое решение x1 = x2 = … = xn = 0. Для нее справедливо, что 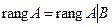 .
.
Теорема Кронекера-Капелли для однородной системы: 1) если 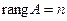 , то система имеет единственное решение – нулевое, 2) если
, то система имеет единственное решение – нулевое, 2) если  , то система имеет бесконечное множество решений, среди которых есть и ненулевые.
, то система имеет бесконечное множество решений, среди которых есть и ненулевые.
Определение.Линейно независимая совокупность решений однородной системы называется фундаментальной системой решений, если каждое решение является линейной комбинацией остальных.
Идея метода Гаусса: матрица системы приводится к трапециевидной или к треугольной форме, затем все получившиеся базисные переменные выражаются через свободные переменные и находится фундаментальное решение системы.
Пример. Решить систему линейных уравнений: 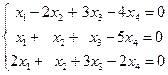 .
.
Решение.Запишемматрицу системы: 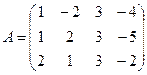
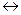
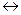
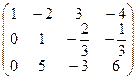
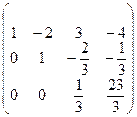
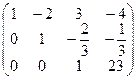 ,
,
отсюда 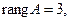 т.к. три ненулевые строки. Количество неизвестных n = 4, т.е.
т.к. три ненулевые строки. Количество неизвестных n = 4, т.е.  , следовательно, по теореме Кронекера - Капелли система имеет бесконечное множество решений. Найдем его. Запишем полученную матрицу в виде системы уравнений:
, следовательно, по теореме Кронекера - Капелли система имеет бесконечное множество решений. Найдем его. Запишем полученную матрицу в виде системы уравнений:
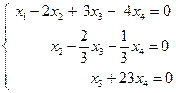 . Система имеет три базисные неизвестные: х1, х2, х3 и одну свободную х4. Выразим базисные неизвестные через свободную переменную, начиная с последнего уравнения:
. Система имеет три базисные неизвестные: х1, х2, х3 и одну свободную х4. Выразим базисные неизвестные через свободную переменную, начиная с последнего уравнения:
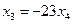 ,
,
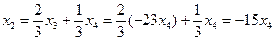 ,
,
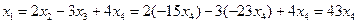 .
.
Ответ: Фундаментальная система решений: 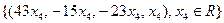 .
.
Дата добавления: 2016-06-15; просмотров: 3191;











