Значащие и верные цифры. Правило округления

Определение численных методов. Погрешности.

Прикладная математика – математическая наука, целью которой является решение прикладных задач: изучение явлений природы, получение их математического описания (математической модели) и его исследование.

Примеры мат.моделей: модель абсолютно твердого тела, модель звездного неба, модель человеческого организма, модели экономических, химических задач и т. д.

Каждая математическая модель содержит некоторые допущения (чем-то пренебрегают).

Основные требования, предъявляемые математическим моделям: 1) адекватность рассматриваемому явлению, 2) сравнительная простота и доступность, 3) необходимость правильной оценки области применения.

Определение. Создание математической модели процесса или явления называется математическим моделированием.

Для решения математических задач используются группы методов: аналитические, графические, численные.

1) Аналитические методы.

Особенность методов состоит в использовании детерминированной информации, строгой алгоритмизации действий и однозначности установленной функциональной зависимости. Для решения задач используются символьные вычисления — это преобразования и работа с математическими равенствами и формулами как с последовательностью символов. Разработкой и реализацией аналитических методов решения математических задач на компьютере занимается компьютерная алгебра, в которой предполагается, что исходные данные, как и результаты решения, сформулированы в аналитическом (символьном) виде. Аналитические решения чаще удаётся получить для наиболее грубых (простых) моделей, реже — для более точных. Аналитические методы основываются на фундаментальной теории математического анализа, функционального анализа, интегральных и дифференциальных исчислений, разработанной группой выдающихся отечественных ученых — А.Н. Колмогоровым, С.В. Фоминым, Л.В. Канторовичем и др.

Недостаток – не всегда можно получить точное решение: многие решения не всегда выражаются в известных функциях или точных методов нахождения решений попросту не существует.

2) Графические методы.

Графические методы считаются весьма важным и эффективным орудием современной науки, они надежно вошли в методику научных исследований.

Недостаток – невысокая точность полученного решения, невозможность построить графики.

3) Численные методы.

Численные методы – раздел прикладной математики.

Определение. Численные (вычислительные) методы — методы решения математических задач в численном виде, иначе, это методы решения задач, сводящиеся к арифметическим и некоторым логическим действиям над числами, при этом результат также получается в виде числовых значений.

Численные методы появились в связи с тем, что искомые решения не всегда выражаются в привычных для нас элементарных или других известных функциях, то есть аналитическим и численным методами отыскать их невозможно. С появлением численных методов появилось решение, но его отыскание было затруднено громоздкими арифметическими операциями над числами, что привело к созданию ЭВМ.

За математическими выражениями в численных методах стоят приближённые численные значения, так как исходные данные в задаче, так и её решения представляются в виде числа или набора чисел. Результат вычислений - также приближенное число. Существуют методы, при помощи которых можно получить и точное решение, например, метод Гаусса для решения систем линейных алгебраических уравнений.

Определение. Численный метод называется сходящимся, если получаемое численное решение задачи очень близко к истинному решению.

Существует достаточно большое количество численных методов, обладающих своими достоинствами и недостатками, которые зависят, прежде всего, от свойств функций, значение которых ищется. Одним из сравнительных показателей качества метода является количество значений функции, которое нужно вычислить для решения задачи с заданной погрешностью. Чем это число меньше, тем при прочих равных условиях эффективнее метод.

Численные методы позволяют получить частные численные решения многих задач, даже сложных математических моделей. К тому же при решении большинства практических задач точное решение не всегда является необходимым.

Как было сказано выше – результатом вычислений с помощью численных методов является приближенные числа.

Определение. Математические действия над приближенными числами называются приближенными вычислениями.

Поэтому главным вопросом является вопрос о погрешности вычислений.

Определение.Погрешность – отклонение точного значения от приближенного.

Источники погрешности – 1)несоответствие математической модели изучаемому явлению, 2) погрешность исходных данных, 3) погрешность метода решения, 4) ошибки округления исходных данных.

Классификация погрешностей – а) неустранимая (источники 1 и 2), b) погрешность метода (источник 3), c) погрешность округления (источник 4)

Пусть а – точное неизвестное числовое значение величины, а^* известное приближенное числовое значение этой величины (приближенное число).

Определение. Число 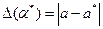называется абсолютной погрешностью округления.

Абсолютная погрешность не полностью характеризует точность измерения. Качество измерения более характеризуется относительной погрешностью.

Определение. Относительной погрешностью называется .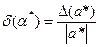

Относительная погрешность безразмерна, часто выражается в процентах.

Любое приближенное число а^* может быть представлено в виде:

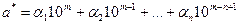, где m – величина разряда или разряд, а 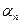- цифра числа. Например, 38, 57 =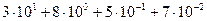

Определяющим точность вычисления является не число десятичных знаков, а число значащих цифр результата.

Определение. Значащими цифрами числа называются все цифры в его записи, начиная с первой ненулевой слева.

Например, 25, 047 – 5 значащих цифр, 0,00250 – 3 значащие цифры.

Определение. Значащая цифра 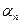приближенного числа а^* называется верной в широком смысле, если абсолютная погрешность не превосходит единицы десятичного разряда, в котором стоит 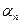: 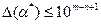, и верной в узком смысле, если 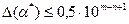. n – число верных цифр в числе. Остальные цифры называются сомнительными.

Пример. Сколько верных цифр содержит число ?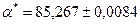

Решение. m = 1, так как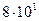

В широком смысле:

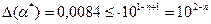, с другой стороны 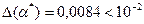, отсюда 2 – n = -2, то есть n = 4. Верные в широком смысле цифры – 8, 5, 2, 6.

В узком смысле:

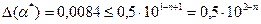, с другой стороны 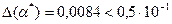, отсюда 2 – n = -1, то есть n = 3. Верные в широком смысле цифры – 8, 5, 2.

Числа 23,56 и 23,5600 как приближенные различны.

Если число записано без указания его абсолютной погрешности, то выписаны только верные цифры.

Употребляя запись 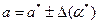надо помнить правило: 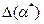выписывать с одной или двумя значащими цифрами, а младший разряд в а^* должен соответствовать младшему разряду в .

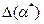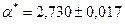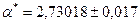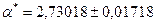- правильно, и - неправильно.

Определение. Число цифр после запятой от первой цифры до последней верной цифры называется числом верных цифр после запятой.

В основе процессов округления числа лежит идея минимальной разности числа а и его округленного значения а^*.

Правило округления (правило четной цифры): если в старшем из отбрасываемых разрядов стоит цифра меньше 5, то содержимое сохраняемых разрядов числа не изменяется. В противном случае в младший сохраняемый разряд добавляется 1 с тем же знаком, что и у самого числа. При этом, если первая слева из отброшенных цифр равна 5, и за ней не следуют отличные от нуля цифры, то последняя оставшаяся цифра усиливается, если она нечетная, и остается без изменений, если она четная.

, , , , .

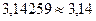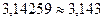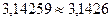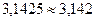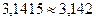Абсолютная погрешность округления не превосходит половины единицы разряда, определяемого последней оставленной значащей цифрой.