Методы Гаусса и простых итераций.

К численным методам линейной алгебры относятся численные методы решения систем линейных алгебраических уравнений, обращения матриц, вычисления определителей, нахождение собственных значений и собственных векторов.

Рассмотрим численные методы решения систем линейных алгебраических уравнений.

Определения. Система уравнений вида 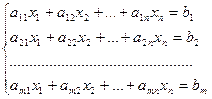называется системой m линейных уравнений с n неизвестными х₁, х₂, …, х_n.

Если все b_i = 0 ( i = 1, 2, 3,…, m), то система называется однородной, в противном случае неоднородной.

Матрица, состоящая из коэффициентов при неизвестных, называется матрицей системы. Матрица, состоящая из коэффициентов при неизвестных и столбца свободных членов, называется расширенной матрицей системы.

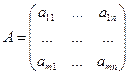– матрица системы, 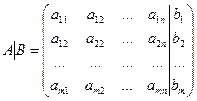– расширенная матрица системы,

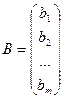– столбец свободных членов, 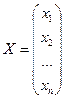– столбец неизвестных.

Матричная запись системы линейных уравнений имеет вид: .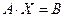

Определение. Система уравнений, имеющая хотя бы одно решение, называется совместной. Система, не имеющая решений, несовместной.

Элементарные преобразования системы (только над строками):

1. перестановка уравнений,

2. умножение уравнения на число, отличное от нуля,

3. прибавление к уравнению другого уравнения, умноженного на число.

Выполняют элементарные преобразования над расширенной матрицей системы и лишь над строками, так как перестановка столбцов соответствует переобозначению неизвестных.

Теорема Кронекера – Капелли.Для того чтобы система m линейных уравнений с n неизвестными была совместной, необходимо и достаточно, чтобы ранг матрицы системы был равен рангу расширенной матрицы. При этом 1) если 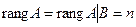, то система имеет единственное решение, 2) если 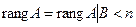, то система имеет бесконечное множество решений. (без доказательства)

Пример 1. Определить, сколько решений имеет система .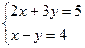

Решение.Найдем ранги матрицы системы и расширенной матрицы системы.

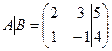
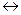
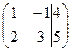
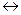
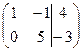
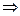две ненулевые строки 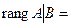2. Если закрыть столбец свободных членов, то получим матрицу системы, которая так же имеет две ненулевые строки, следовательно, 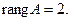Число неизвестных – два: x, y. Получили, что 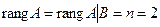, следовательно, система имеет единственное решение.

Пример 2. Определить, сколько решений имеет система уравнений .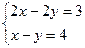

Решение.Найдем ранги матрицы системы и расширенной матрицы системы.

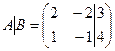
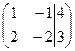
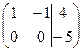
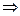две ненулевые строки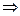 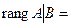2. Если закрыть столбец свободных членов, то получим матрицу системы, которая имеет одну ненулевую строку, следовательно, 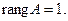Получили, что 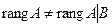, следовательно, система не имеет решений.

Численные методы решения систем линейных алгебраических уравнений бывают1) точными или прямыми, 2) приближенными или итерационными.

Точные или прямые методы – это алгоритмы, позволяющие получить точное решение системы за конечное число арифметических действий (правило Крамера, метод Гаусса, метод прогонки).

Достоинства: используют конечные соотношения, то есть формулы для вычисления неизвестных; сравнительно просты и наиболее универсальны: пригодны для широкого класса линейных систем. Недостаток: требуют хранения в оперативной памяти ЭВМ большого количества численных значений (занимает много места в памяти); в процессе решения накапливаются погрешности, так как вычисления на любом этапе используют результаты предыдущих операций.

Итерационные или приближенные методы – методы последовательных приближений к решению, в результате которых получается приближенное решение (метод простых итераций, метод Зейделя, релаксаций).

Достоинства: требуют небольшого объема памяти ЭВМ; погрешности в процессе вычислений не накапливаются, так как точность вычислений на каждом шаге определяется лишь результатом предыдущей операции; могут использоваться для уточнения решений, полученных с помощью прямых методов.

Метод Гаусса

Это прямой численный метод, применяемый для нахождения решения однородных и неоднородных систем, когда )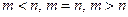

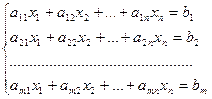- неоднородная, 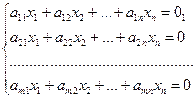- однородная.

Идея метода – последовательное исключение неизвестных: с помощью элементарных преобразований над строками расширенная матрица системы приводится к трапециевидной или к треугольной форме, при этом удобнее, чтобы все ведущие элементы были равны 1 (алгоритм нахождения рангов), либо устанавливается, что система несовместна. Это прямой ход метода Гаусса.