Продольная жесткость стержня

с = ЕА/l, (2.16)

где Е = 2,1×10¹¹ Па — модуль продольной упругости материала; А — площадь поперечного сечения, м².

Податливость стержня

е= l/ЕА.

Жесткость канатного полиспаста

,

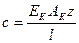где Ек = 1,2×10¹¹ Па — модуль продольной упругости каната; Ак — площадь поперечного сечения проволок каната; z — число ветвей полиспаста; l — длина полиспаста.

Поперечная жесткость балок зависит от способа закрепления и приведена в курсах сопротивления материалов. Например, жесткость консольной балки

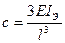, (2.17)

где I_Э — экваториальный момент инерции сечения, м⁴; l — длина балки, м.

Крутильная жесткость характеризуется коэффициентом жесткости с при кручении, представляющем собой крутящий момент М_КР, закручивающий вал на угол j = 1 рад (Н×м/рад):

с = М_КР/j (2.18)

М_КР = сj

Жесткость круглого вала

,

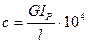где 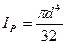- полярный момент инерции сечения вала диаметром d; l — длина закручиваемого участка вала.

При расчетах более удобно пользоваться коэффициентом податливости (в дальнейшем будем называть податливостью). Общая податливость детали равна сумме податливостей отдельных ее участков.

Расчет динамических нагрузок в упругих связях для различных случаев нагружения. После расчета параметров приведенной системы определяем динамические нагрузки в упругих связях механизмов.

Рассмотрим динамические нагрузки в двухмассовой системе с линейной жесткостью с и массами m₁ и m₂, на которые действуют силы движущие F и вес груза G (рисунок 2.2). К такой системе можно привести механизмы подъема, где жесткость канатов полиспастов намного меньше жесткости самого привода, ленточные и цепные конвейеры и др.

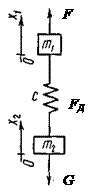Рисунок 2.2 – Эквивалентная двухмассовая схема механизма

Под действием внешних сил в неустановившийся период в упругой системе возникают колебательные процессы, которые можно описать следующей системой дифференциальных уравнений движения масс:

(2.19)

где х₁, х₂ — перемещение соответственно первой и второй масс.

Силу G берут со знаком «минус» как силу сопротивления.

В уравнениях (2.19) первые слагаемые — силы инерции соответствующей массы, вторые — силы упругости в связи; в правой части уравнений — силы, действующие на систему в период неустановившегося движения.

Умножив первое уравнение (2.19) на m₂, второе — на m₁ вычтя второе из первого и разделив на m₁m₂, получим

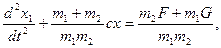(2.20)

где х = х₁-х₂ — разность перемещений масс.

Дифференциальное уравнение (2.20) характеризует деформацию упругого звена или динамическое усилие в нем при условии, что

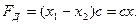(2.21)

Решив уравнение (2.20) и учитывая условие (2.21), получим уравнение для определения динамических усилий в упругой связи:

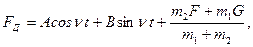(2.22)

где А, В – постоянные интегрирования или амплитуды колебаний динамических нагрузок; n - собственная частота колебаний. Для двухмассовой системы:

(2.23)

Период собственных колебаний

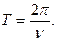(2.24)

Постоянные А и В находят из начальных условий. При нулевых условиях ( 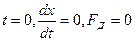) постоянные будут:

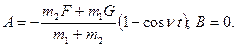(2.25)

Подставив постоянные А и В в уравнение (2.21), получим формулу для определения динамических усилий в упругой связи:

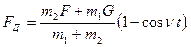(2.26)

Обозначим постоянную составляющую нагрузок, равную сумме статических и инерционных (от массы m₂) нагрузок, через F_П:

(2.27)

где - коэффициенты распределения масс в системе.

Тогда уравнение (2.26) можно записать в таком простом виде:

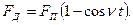(2.28)

Для расчета динамики механизмов передвижения, поворота и других реальную систему целесообразно приводить к крутильной расчетной схеме (рисунок 2.3). Для двухмассовой системы дифференциальные уравнения движения масс, совершающих крутильные колебания, можно записать в виде:

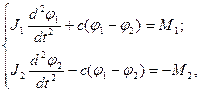(2.29)

где J₁ — общий момент инерции вращающихся масс привода (ротора, тормозного шкива, муфт); J₂ — приведенный к валу двигателя момент инерции второй массы — поступательно и вращательно движущихся частей крана; j₁, j₂ — углы закручивания первой и второй масс; с — приведенная крутильная жесткость линии передач; М₁ — пусковой (тормозной) момент электродвигателя (тормоза); М₂ — момент сопротивления движению крана.

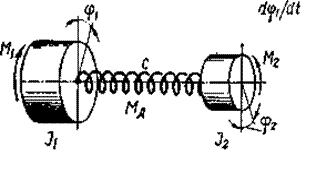Рисунок 2.3 – Эквивалентная двухмассовая крутильная схема механизма

Моменты инерции масс и силовые моменты необходимо привести к валу двигателя или ходовых колес.

При нулевых начальных условиях

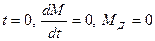
момент сил упругости в линии передач привода

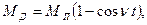(2.30)

где

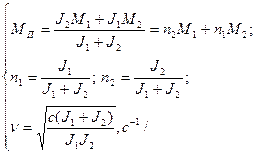(2.31)

Аналогично можно определить – динамические нагрузки при торможении механизма, подставив вместо М₁ тормозной момент М_Т. Динамические нагрузки при торможении, как правило, больше, чем при пуске привода.

Из уравнения (2.31) следует, что максимальные моменты сил упругости в приводной линии равны удвоенному значению статических и инерционных нагрузок. Однако действительные системы механизмов многомассовые с зазорами в соединениях. Поэтому динамические нагрузки в их приводах во много раз превышают статические нагрузки от сил сопротивления. Особенно интенсивные колебания возникают в механизме при резких торможениях короткоходовым тормозом или при противовключении электродвигателя.