Жёсткость конструкций
Жесткость определяет работоспособность конструкции в такой же (а иногда и в большей) мере, как и прочность. Повышенные деформации могут нарушить нормальную работу конструкции задолго до возникновения опасных для прочности напряжений. Нарушая равномерное распределение нагрузки, они вызывают сосредоточение усилий на отдельных участках деталей, в результате чего появляются местные высокие напряжения, иногда значительно превосходящие величину номинальных напряжений.
Нежесткость корпусов расстраивает взаимодействие расположенных в них механизмов, вызывая повышенное трение и износ подвижных сочленений. Нежесткость валов и опор зубчатых передач нарушает правильное зацепление колес и приводит к быстрому износу зубьев. Нежесткость цапф и опор подшипников скольжения вызывает повышенные кромочные давления, появление очагов полужидкостного и полусухого трения, перегрев, заедание или снижение срока службы подшипников. Нежесткость неподвижных соединений, подверженных действию динамических нагрузок, вызывает фрикционную коррозию, наклеп и сваривание поверхностей.
У машин-орудий жесткость рабочих органов определяет точность размеров обрабатываемых изделий. В металлорежущих станках точность обработки зависит от жесткости станин и рабочих органов, в прокатных станах точность проката — от жесткости клетей и валков.
Жесткость имеет большое значение для машин облегченного класса (транспортные машины, стрелы кранов и экскаваторов). Стремясь облегчить конструкцию и максимально использовать прочностные ресурсы материалов, конструктор в данном случае повышает уровень напряжения, что сопровождается увеличением деформаций. Широкое применение равнопрочных, наиболее выгодных по массе конструкций, в свою очередь, вызывает увеличение деформаций, так как равнопрочные конструкции наименее жесткие.
Особую остроту приобретают вопросы жесткости в связи с появлением высокопрочных и сверхпрочных материалов, применение которых обусловливает резкое увеличение деформативности конструкций.
Нередки случаи недооценки величины усилий, действующих на конструкцию. Очень часто при расчете получают ничтожные величины рабочих усилий, а фактически же неожиданно возникают нагрузки, приводящие к поломкам и выходу из строя деталей. Эти нагрузки могут быть вызваны неточностями монтажа, деформацией недостаточно жестких элементов конструкции, остаточными деформациями, перетяжкой крепежных деталей, повышенным трением и перекосами трущихся частей узла, усилиями, возникающими при транспортировке и установке машины, и другими факторами, не учитываемыми расчетом.
Величину деформаций можно рассчитать лишь в простейших случаях методами сопротивления материалов и теории упругости. В большинстве случаев приходится иметь дело с нерасчетными деталями, сечения которых определяются условиями изготовления (например, технологией литья) или имеющими сложную конфигурацию, затрудняющую определение напряжений.
Здесь приходится прибегать к моделированию, эксперименту, опыту имеющихся аналогичных конструкций, а нередко полагаться только на чутье, вырабатывающееся с течением времени у конструктора. Опытный конструктор, зная направление и величину действующих усилий, оценивает более или менее правильно направление и величину деформации, выявляет слабые места и, пользуясь разнообразными приемами, увеличивает жесткость, компонуя рациональную конструкцию. Напротив, конструкции, спроектированные начинающими конструкторами, обычно страдают недостатком жесткости.
Критерии жёсткости
Жесткость — это способность системы сопротивляться действию внешних нагрузок с наименьшими деформациями. Для машиностроения можно сформулировать следующее определение: жесткость — это способность системы сопротивляться действию внешних нагрузок с деформациями, допустимыми без нарушения работоспособности системы. Понятием, обратным жесткости, является упругость, т.е. свойство системы приобретать относительно большие деформации под действием внешних нагрузок. Для машиностроительных конструкций наибольшее значение имеет жесткость. Однако в ряде случаев важным свойством оказывается и упругость (пружины, рессоры и другие упругие детали).
Жесткость оценивают коэффициентом жесткости, представляющим собой отношение силы Р, приложенной к системе, к максимальной деформации f, вызываемой этой силой.
Для случая растяжения-сжатия бруса постоянного сечения в пределах упругой деформации, коэффициент жесткости согласно закону Гука
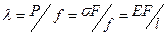 , (5.1)
, (5.1)
где F - сечение бруса, мм2; l - длина бруса в направлении действия силы, мм.
Обратную величину
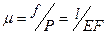 (5.2)
(5.2)
характеризующую упругую податливость бруса называют коэффициентом упругости.
Определенный по относительной деформации ( 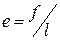 ) коэффициент жесткости
) коэффициент жесткости 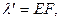 (5.3)
(5.3)
представляет собой условную нагрузку в (Н), вызывающую относительную деформацию е = 1. Соответствующий коэффициент упругости
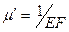 (5.4)
(5.4)
представляет собой относительную деформацию при приложении нагрузки 1Н .
Для случая кручения бруса постоянного сечения коэффициент жесткости равен отношению приложенного к брусу крутящего момента Т к вызываемому этим моментом углу 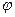 [рад] поворота сечений бруса на длине l [мм], где Jp — полярный момент инерции сечения бруса.
[рад] поворота сечений бруса на длине l [мм], где Jp — полярный момент инерции сечения бруса.
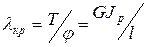 , (5.5)
, (5.5)
Для случая изгиба бруса постоянного сечения коэффициент жесткости
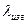
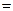
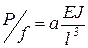 (5.6)
(5.6)
где J - момент инерции сечения бруса, мм4; l - длина бруса, мм;
а — коэффициент, зависящий от условий нагружения.
Таблица 5.1 Жёсткость при различных схемах изгиба
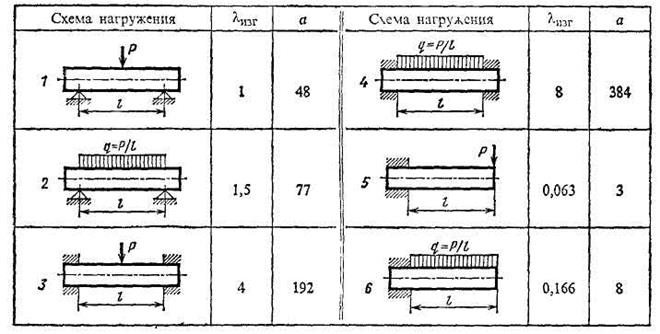
В табл. 5.1 приведены значения коэффициента жесткости для нескольких случаев нагружения изгибом. За единицу принято значение 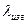 ,соответствующее изгибу двухопорного бруса, нагруженного сосредоточенной силой Р в середине пролета.
,соответствующее изгибу двухопорного бруса, нагруженного сосредоточенной силой Р в середине пролета.
Как видно из табл. 5.1, жесткость системы сильно зависит от условий приложения нагрузки. Брус, нагруженный равномерно распределенной нагрузкой, обладает в 1,5 раза большей жесткостью, чем брус, нагруженный сосредоточенной нагрузкой той же суммарной величины. Еще большее влияние на жесткость имеют тип и расположение опор. Например, жесткость двухопорного бруса с заделанными концами в 4-8 раз превышает жесткость бруса, свободно опертого по концам. Жесткость консольного бруса, нагруженного сосредоточенной силой, составляет только 0,063 жесткости двухопорного бруса той же длины, нагруженного той же силой посредине пролета.
При заданной величине нагрузки и заданных линейных размерах системы жесткость вполне определяется величиной максимальной деформации f. Эту величину часто применяют для практической оценки деформативности геометрически одинаковых систем.
Факторы, определяющие жёсткость конструкций
Жесткость конструкций определяют следующие факторы:
модуль упругости материала (модуль нормальной упругости Е при растяжении-сжатии и изгибе, модуль сдвига G — при кручении);
геометрические характеристики сечения деформируемого тела (сечение F при растяжении-сжатии, момент инерции J при изгибе, полярный момент инерции Jp при кручении); линейные размеры деформируемого тела (длина l); вид нагрузки и тип опор [фактор а в формуле (5.1)].
Модуль упругости является устойчивой характеристикой металлов, мало зависит от термообработки и содержания (в обычных количествах) легирующих элементов и определяется лишь плотностью атомно-кристаллической решетки основного компонента. Из технических металлов только W, Мо и Be имеют повышенный модуль упругости (соответственно Е= 40, 35 и 31*104 МПа).
Однако применение того или иного материала по большей части определяется условиями работы детали. Поэтому главным практическим средством увеличения жесткости является маневрирование геометрическими параметрами системы.
На жесткость сильно влияют размеры и форма сечений. В случае растяжения-сжатия жесткость пропорциональна квадрату, а при изгибе — четвертой степени размеров сечения (в направлении действия изгибающего момента).
Влияние линейных размеров детали невелико для случая растяжения-сжатия (жесткость обратно пропорциональна первой степени длины)и очень значительна при изгибе (жесткость обратно пропорциональна третьей степени длины).
Конструктивные, факторы, влияющие на жесткость, можно объединить в показателях [см. формулы (5.1), (5.6)]: при растяжении-сжатии 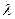 = F/l, при изгибе
= F/l, при изгибе 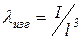 . Для бруса круглого сечения в случае растяжения-сжатия
. Для бруса круглого сечения в случае растяжения-сжатия 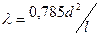 и в случае изгиба
и в случае изгиба 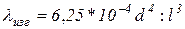 . Условие равножесткости для брусьев с различными значениями l и d, нагруженных одинаковой силой Р: при растяжении-сжатии d2/l= const, при изгибе d4/l3 = const. На жесткость конструкции косвенно влияет прочность материала. При прочих равных условиях деформации пропорциональны напряжениям. Но величину напряжений принимают, как правило, пропорционально прочности материала; напряжения представляют собой отношение предела прочности (или предела текучести) к коэффициенту надежности. Следовательно, чем выше прочность материала, тем больше величина принимаемых напряжений и при прочих равных условиях больше деформация системы. Напротив, чем меньше запас прочности и ближе величина действующих в системе напряжений к пределу прочности, тем больше деформация и меньше жесткость системы.
. Условие равножесткости для брусьев с различными значениями l и d, нагруженных одинаковой силой Р: при растяжении-сжатии d2/l= const, при изгибе d4/l3 = const. На жесткость конструкции косвенно влияет прочность материала. При прочих равных условиях деформации пропорциональны напряжениям. Но величину напряжений принимают, как правило, пропорционально прочности материала; напряжения представляют собой отношение предела прочности (или предела текучести) к коэффициенту надежности. Следовательно, чем выше прочность материала, тем больше величина принимаемых напряжений и при прочих равных условиях больше деформация системы. Напротив, чем меньше запас прочности и ближе величина действующих в системе напряжений к пределу прочности, тем больше деформация и меньше жесткость системы.
Наиболее простой способ уменьшения деформаций заключается в уменьшении уровня напряжений. Однако этот путь нерационален, так как он сопряжен с увеличением массы конструкции. В случае изгиба рациональным способом уменьшения деформаций является целесообразный выбор формы сечений, условий нагружения, типа и расстановки опор. Поскольку влияние линейных параметров системы при изгибе велико [формула (5.6)], то в данном случае имеются эффективные способы увеличения жесткости, позволяющие уменьшить деформации системы в десятки раз по сравнению с исходной конструкцией, а иногда практически полностью ликвидировать изгиб.
В случае кручения эффективными средствами повышения жесткости являются уменьшение длины детали на участке кручения и, особенно, увеличение диаметра, так как полярный момент инерции возрастает пропорционально четвертой степени диаметра. В случае растяжения-сжатия возможность увеличения жесткости гораздо меньше, так как форма сечения не играет никакой роли, а деформации зависят только от площади сечения, которая определяется условием прочности. Единственным способом повышения жесткости здесь является уменьшение длины детали. Если же длина задана, то остается только переход на материалы с более высоким модулем упругости.
Величина деформации зависит не только от максимального действующего в системе напряжения в опасном сечении детали, но и от закона распределения напряжений по всем остальным сечениям, т. е. от формы детали по ее длине. Равнопрочные детали (у которых максимальные напряжения во всех сечениях одинаковы) обладают наименьшей жесткостью.
Жесткость за пределами упругих деформаций. На практике приходится учитывать возможность появления пластических деформаций. Даже в системах, рассчитанных на работу в пределах упругости, нередко возникают местные пластические деформации в слабых местах конструкции, на участках концентрации напряжений и в элементах, неблагоприятно расположенных относительно действующих сил, и т. д. Общие или местные пластические деформации могут возникнуть на перегрузочных режимах. Важно, чтобы эти деформации не нарушали работоспособность детали.
Жесткость тонкостенных и составных конструкций. В тонкостенных, в частности оболочковых, конструкциях особое значение имеет устойчивость системы. Конструкции такого рода склонны в известных условиях при напряжениях, безопасных с точки зрения номинального расчета на прочность и жесткость, подвергаться резким местным или общим деформациям, носящим характер внезапного крушения.
Главным средством борьбы с потерей устойчивости (наряду с повышением прочности материала) является усиление легко деформирующихся участков системы введением местных элементов жесткости или связей между деформирующимися участками и узлами жесткости.
В составных конструкциях (в системах из нескольких деталей, соединенных на неподвижных посадках) жесткость зависит также от такого фактора, редко учитываемого, но имеющего на практике большое значение, как жесткость узлов сопряжения. Наличие зазоров в узлах сопряжения приводит к появлению деформаций, иногда во много раз превосходящих собственные упругие деформации элементов конструкции. В подобных узлах следует обращать особое внимание на жесткость крепления и заделки деталей.
Эффективными способами увеличения жесткости составных систем являются силовая затяжка узлов сочленения, посадка с натягом, увеличение опорных поверхностей и придание деталям повышенной жесткости на участках сопряжения.
5.2 Удельные показатели жёсткости
При сравнении жесткости, прочности и массы деталей, изготовленных из различных материалов, следует различать четыре основных случая:
1. Детали одинаковы по конфигурации (при равной нагрузке имеют одинаковые напряжения);
2. Детали равножесткие (имеют одинаковые деформации при различных сечениях и напряжениях);
3. Детали равнопрочные (имеют одинаковый запас надежности, различные сечения и напряжения, пропорциональные пределу прочности материала) ;
4. Детали имеют одинаковую массу.
Первый случай (замена материала детали другим без изменения ее геометрических размеров) практически встречается, когда сечения детали заданы технологическим процессом (например, литые корпусные детали). Это также случай нерасчетных деталей с неопределенными напряжениями. Второй и третий случай имеют место при замене материала детали другим с одновременным изменением ее сечений (расчетные детали, в которых напряжения и деформации определяются достаточно точно и назначаются с расчетом максимального использования прочности и жесткости материала). Четвертый случай — это случай, когда масса конструкции задана ее функциональным назначением и условиями эксплуатации.
При сравнении прочностных, массовых и жесткостных показателей деталей, изготовленных из различных материалов, будем предполагать, что длина деталей одинакова, а сечения в последних трех случаях изменяются геометрически подобно.
1. Детали одинаковой конфигурации (а = const). В случае растяжения-сжатия относительный коэффициент жесткости согласно формуле (5.3) 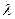 = EА, где А — сечение детали; Е — модуль нормальной упругости.
= EА, где А — сечение детали; Е — модуль нормальной упругости.
По условию F= const. Следовательно, 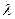 = const E т.е. жесткость деталей в данном случае зависит только от величины модуля упругости. Запас надежности
= const E т.е. жесткость деталей в данном случае зависит только от величины модуля упругости. Запас надежности
n = 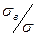 , где
, где 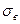 — предел прочности нарастяжение;
— предел прочности нарастяжение; 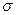 — действующее в детали напряжение. По условию
— действующее в детали напряжение. По условию 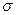 = const. Следовательно, п = const
= const. Следовательно, п = const 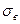 Масса детали
Масса детали
G = yАl = const 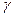 , где
, где 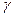 — плотность материала. Совершенно аналогичны соотношения в случае изгиба и кручения, той лишь разницей, что при кручении жесткость детали определяется «величиной модуля сдвига.
— плотность материала. Совершенно аналогичны соотношения в случае изгиба и кручения, той лишь разницей, что при кручении жесткость детали определяется «величиной модуля сдвига.
2. Равножесткие детали ( 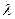 = const). Условие равножесткости в случае растяжения-сжатия согласно формуле (5.1)
= const). Условие равножесткости в случае растяжения-сжатия согласно формуле (5.1) 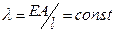
Следовательно, 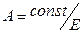 (5.7)
(5.7)
Масса равножестких деталей 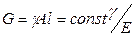 .
.
Напряжения 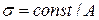 .
.
С учетом выражения (5.7) 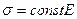 , запас надёжности
, запас надёжности 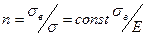 .
.
При изгибе масса равножёстких деталей 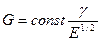 .
.
Запас надежности 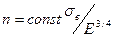 .
.
3. Равнопрочные детали (n = const). Условие равнопрочности при растяжении-сжатии 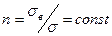 .
.
Ввиду того, что 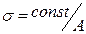 ,
, 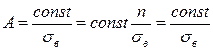 (5.8)
(5.8)
и масса 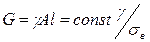 ;
;
Коэффициент жесткости с учетом формулы (5.8) 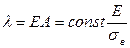 .
.
При изгибе 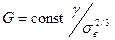 ;
; 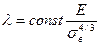 .
.
4. Детали равной массы (G = const). Условие равной массы при растяжении-сжатии G = 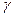 Аl = const. Следовательно, А = const/
Аl = const. Следовательно, А = const/ 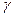 .
.
Напряжения 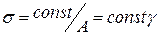 . Запас надёжности
. Запас надёжности 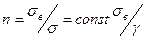 .
.
Коэффициент жёсткости 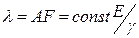 . При изгибе
. При изгибе 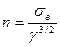 ;
; 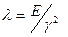 .
.
Для сравнительных целей пользуются наиболее простыми формулами для растяжения-сжатия.
Показатели массы, жесткости и прочности при растяжении-сжатии для всех разобранных выше случаев приведены в табл.5.2. Значения удельной прочности n/G = 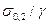 и удельной жесткости
и удельной жесткости 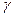 /G = Е/
/G = Е/ 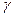 одинаковы для всех категорий деталей.
одинаковы для всех категорий деталей.
Таблица 5.2 . Характеристики массы, прочности и жесткости
| Детали | Масса, G | Прочность, п | Жесткость, 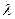
|
| Одинаковой конфигурации | 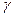
| 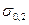
| Е |
| Равножесткие | у/Е | 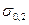 /Е /Е
| const |
| Равнопрочные | 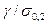
| const | Е/ 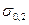
|
| Равной массы | const | 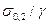
| E/ 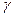
|
5.3 Конструктивные способы повышения жёсткости[36]
Главные конструктивные способы повышения жесткости без существенного увеличения массы:
всемерное устранение изгиба, замена его растяжением или сжатием;
для деталей, работающих на изгиб, — целесообразная расстановка опор, исключение невыгодных по жесткости видов нагружения;
рациональное, не сопровождающееся возрастанием массы, увеличение моментов инерции сечений;
рациональное усиление ребрами, работающими предпочтительно на сжатие;
усиление заделочных участков и участков перехода от одного сечения к другому;
блокирование деформаций введением поперечных и диагональных связей;
привлечение жесткости смежных деталей;
для деталей коробчатого типа — применение скорлупчатых, сводчатых, сферических, яйцевидных и тому подобных форм;
для деталей типа дисков — применение конических, чашечных, сферических форм; рациональное оребрение, гофрирование;
для деталей типа плит — применение арочных, коробчатых, двутельных, ячеистых и сотовых конструкций.
Замена изгиба растяжением-сжатием
Повышенная жесткость деталей, работающих на растяжение-сжатие, в конечном итоге обусловлена лучшим использованием материала при этом виде нагружения. В случае изгиба и кручения нагружены преимущественно крайние волокна сечения. Предел нагружения наступает, когда напряжения в них достигают опасных значений, тогда как сердцевина остается недогруженной. При растяжении-сжатии напряжения одинаковы по всему сечению; материал используется полностью. Предел нагружения наступает, когда напряжения во всех точках сечения теоретически одновременно достигают опасного значения. Кроме того, при растяжении-сжатии деформации детали пропорциональны первой степени ее длины. В случае же изгиба действие нагрузки зависит от расстояния между плоскостью действия изгибающей силы и опасным сечением; деформации здесь пропорциональны третьей степени длины.
Сравним консольную балку круглого сечения (d = 20 мм), нагруженную изгибающей силой Р (рис. 5.3.1), и треугольную ферму с одинаковым вылетом l, составленную из стержней того же диаметра. Верхний стержень фермы под действием силы Р работает на растяжение, нижний - на сжатие. При соотношениях, показанных на рисунке, максимальное напряжение изгиба в балке в 550 раз больше напряжений в стержнях фермы, а максимальная деформация (в точке приложения силы Р) больше в 9 *103 раз.
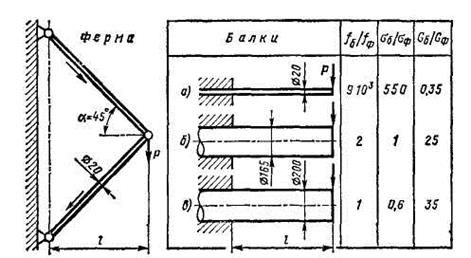
Рис. 5.3.1
Жёсткость, прочность и масса треугольной ферменной системы и консольных балок
Для того,чтобы сделать системы равнопрочными, необходимо увеличить диаметр балки до 165 мм (рис. 5.3.1, б). При этом масса балки (не считая заделочного участка) становится в 25 раз больше массы фермы, а максимальный прогиб оказывается в 2 раза больше прогиба фермы.
Для достижения одинаковой жесткости (равенство максимальных прогибов) необходимо увеличить диаметр балки до 200 мм (рис. 5.3.1, в). Напряжения снижаются, составляя 0,6 величины напряжений в стержнях фермы.
Связь между прогибом fб консольной балки круглого сечения в плоскости приложения силы и прогибом fф ферменной системы при одинаковых сечениях можно выразить соотношением 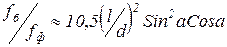 ,
,
где l - длина вылета; d — диаметр стержней балки и фермы; а - половина угла при вершине ферменного треугольника.
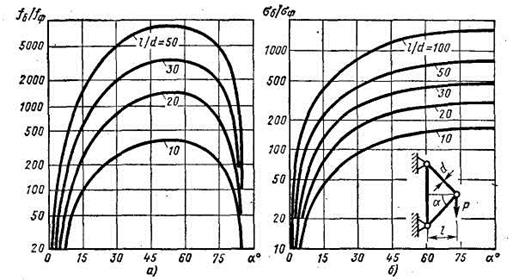 Отношение fб / fф в функции угла а для различных значений l/d приведено на рис. 5.3.2, а. При одинаковости сечений прогиб консольной балки может быть в сотни .и тысячи раз больше прогиба ферменной системы. Разница резко возрастает с увеличением отношения l/d, т. е. относительным утонением стержней. Однако и для наиболее жестких стержней (l/d = 10) разница в пользу ферменной системы весьма велика.
Отношение fб / fф в функции угла а для различных значений l/d приведено на рис. 5.3.2, а. При одинаковости сечений прогиб консольной балки может быть в сотни .и тысячи раз больше прогиба ферменной системы. Разница резко возрастает с увеличением отношения l/d, т. е. относительным утонением стержней. Однако и для наиболее жестких стержней (l/d = 10) разница в пользу ферменной системы весьма велика.
Рис.5.3.2
Сравнительные характеристики консольной балки и треугольной ферменной системы
Отношение fб / fф имеет пологий максимум при а = 45 — 60°. В этом диапазоне фермы типа, приведенного на рис. 5.3.1, обладают наибольшей жесткостью. Напряжения (рис. 5.3.2, б) в балке во много раз больше напряжений в стержнях (например, при а = 45° в 100 — 1000 раз).
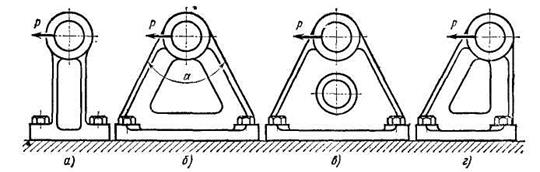
Рис. 5.3.3
Конструкции литых кронштейнов
Конструктивную аналогию системам, изображенным на рис. 5.3.1, представляет литой кронштейн (рис. 5.3.3). Жесткость узлов соединения стержней в раскосном кронштейне видоизменяет условия их работы по сравнению с чистой фермой, в которой стержни соединены шарнирами; все же в случае раскосного кронштейна (рис. 5.3.3, б) стержни работают преимущественно на растяжение-сжатие, тогда как балочный кронштейн (рис. 5.3.3, а) подвергается изгибу. Конструкция становится еще более прочной и жесткой, если стержни кронштейна соединить сплошной перемычкой', связывающей их в жесткую систему (рис. 5.3.3, в).
Кронштейн ферменного типа с вертикальным верхним стержнем (рис.5.3.3, г)значительно менее жесткий, чем кронштейн на рис. 5.3.3, б, так как конец вертикального стержня под нагрузкой перемещается приблизительно по направлению действия силы и для ограничения деформаций его жесткость не используется.
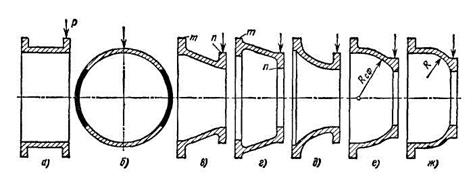
Рис. 5.3.4
Консольные тонкостенные системы
В тонкостенном цилиндрическом отсеке, несущем поперечную нагрузку Р (рис. 5.3.4, а), все участки, расположенные по образующим, подвергаются изгибу. Нагрузку воспринимают преимущественно боковые стенки (рис. 5.3.4, б), параллельные плоскости действия изгибающего момента (зачернены на рисунке), так как их жесткость в этом направлении во много раз больше жесткости стенок, расположенных перпендикулярно плоскости действия момента.
При конической форме (рис. 5.3.4, в, г), приближающей конструкцию к ферменной (рис. 5.3.1), стенки конуса, расположенные в плоскости действия изгибающего момента, работают: верхние на растяжение, а нижние подобно подкосу — на сжатие. Боковые стенки испытывают преимущественно изгиб; их жесткость соизмерима с жесткостью верхних и нижних стенок. Следовательно, при конической форме стенки отсека полностью включаются в работу; прочность и жесткость конструкции увеличиваются.
Связь между растянутыми и сжатыми стенками осуществляют кольца жесткости т, п, которые помимо силового замыкания предотвращают овализацшо конуса под действием нагрузки. Такие кольца являются непременным условием правильной работы тонкостенных отсеков.
Близки к конусам по жесткости тюльпанные (рис. 5.3.4, д), сферические (рис. 5.3.4, е), тороидные (рис. 5.3.4, ж) и аналогичные формы.
Еще пример устранения напряжений изгиба показан на рис. 5.3.5. Здесь двухопорная балка, подвергающаяся изгибу (рис. 5.3.5, а), заменена более выгодной стержневой системой (рис. 5.3.5, б), наклонные стержни которой работают на сжатие, а горизонтальные — на растяжение. Близка к этому случаю арочная балка (рис. 5.3.5, в), работающая также преимущественно на сжатие.
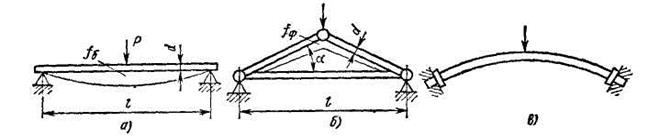 Рис. 5.3.5. Схемы свободно опертой балки (а), стержневой системы (б), и арочной балки (в)
Рис. 5.3.5. Схемы свободно опертой балки (а), стержневой системы (б), и арочной балки (в)
Блокирование деформаций
Вобщей постановке вопроса задача увеличения жесткости заключается в том, чтобы найти точки наибольших перемещений системы, деформируемой под действием нагрузки, и предотвратить эти перемещения введением элементов растяжения-сжатия, расположенных по направлению перемещений. Классическим примером решения этой задачи является увеличение жесткости рам и ферменных конструкций раскосами.
Жесткость стержневой рамы, подвергающейся действию сдвигающих сил Р (рис. 5.3.6, д), крайне незначительна и определяется только сопротивлением вертикальных стержней изгибу и жесткостью узлов соединения стержней. Введение косынок (рис. 5.3.6, б), приближает схему работы стержней к схеме работы заделанных балок и несколько уменьшает деформации.
Наиболее эффективно введение диагональных связей (раскосов), работающих на растяжение или сжатие. Раскос растяжения (рис. 5.3.6, в) должен при перекосе рамы удлиниться на величину ∆. Так как жесткость растягиваемого стержня во много раз больше изгибной жесткости вертикальных стержней, то общая жесткость системы резко возрастает. Аналогично действует раскос сжатия (рис. 5.3.6, г). Но в этом случае необходимо считаться с возможностью продольного изгиба сжатого стержня, что делает систему менее желательной.
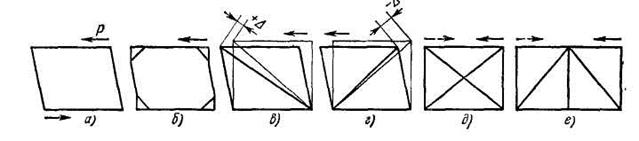
Рис. 5.3.6. Схемы действия диагональных связей
Если нагрузка действует попеременно в обоих направлениях, то применяют раскосы перекрестные или чередующегося направления (рис. 5.3.6, д и ё).
В порядке возрастающей жесткости на рис. 5.3.7, а…и представлены схемы плоских ферм и на рис. 5.3.7, к..н — сложных плоских ферм с усиливающими элементами, предотвращающими продольный изгиб и потерю устойчивости стержней.
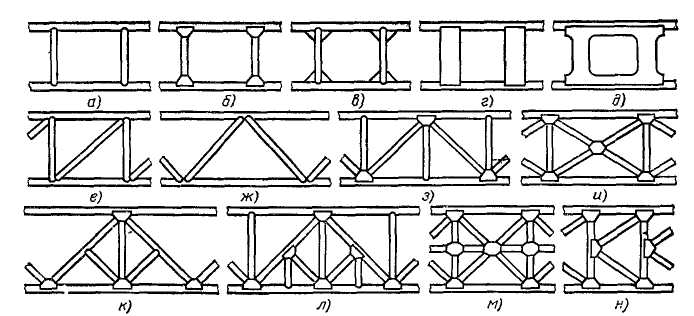
Рис. 5.3.7. Плоские фермы
Консольные и двухопорные системы
Если по конструкции и функциональному назначению детали нельзя избежать изгиба, то на первый план выступает задача уменьшения деформаций и напряжений изгиба.
На рис. 5.3.8 изображены основные схемы изгиба балок: консольной (а), опертой по концам (б) и с заделанными концами (в).
Из сопоставления величин максимальных изгибающих моментов и прогибов видно большое преимущество двухопорных балок в сравнении с консольной по жесткости и прочности. При одинаковых длине сечении балок и нагрузке максимальный изгибающий момент (а следовательно, и максимальные напряжения изгиба) в двухопорной балке в 4 раза а в двухопорной (заделанной) в 8 раз меньше, чем в консольной. Еще больше преимущества по жесткости. Максимальный прогиб двухопорной балки в 16 раз, а двухопорной заделанной - в 64 раза меньше, чем консольной. Практически различие между двухопорными и консольными деталями выражено не так резко, как в приведенном схематическом сравнении. В сравнимых конструктивных вариантах консольной и двухопорной балок длина консоли редко бывает равной расстоянию между опорами в двухопорной балке; чаще всего она значительно меньше.
В консольной (г) и двухопорной (д) установке вала-шестерни по габаритным условиям расстояние между опорами в двухопорной установке не удается сделать меньшим 2l, вследствие чего оба варианта приходится сравнивать на базе различных, а не одинаковых, как в предыдущем случае, длин.
Максимальный изгибающий момент при двухопорной установке в 2 раза меньше, чем в консольной. Выигрыш в максимальных напряжениях изгиба гораздо больше, потому что момент сопротивления в опасном сечении (в плоскости действия силы Р) двухопорного вала значительно больше момента сопротивления в опасном сечений (в плоскости переднего, ближайшего к нагрузке подшипника) консольного вала. При соотношениях, приведенных под рис. 5.3.8, напряжения в опасном сечении двухопорного вала в 5 раз меньше, чем в консоли.
Максимальный прогиб двухопорного вала формально в 2 раза меньше прогиба консольного вала, а если учесть большую величину момента инерции 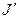 сечения двухопорного вала по сравнению с моментом инерции J консольного вала, то фактически еще меньше (при соотношениях, приведенных под рисунком — в 6,5 раза).
сечения двухопорного вала по сравнению с моментом инерции J консольного вала, то фактически еще меньше (при соотношениях, приведенных под рисунком — в 6,5 раза).
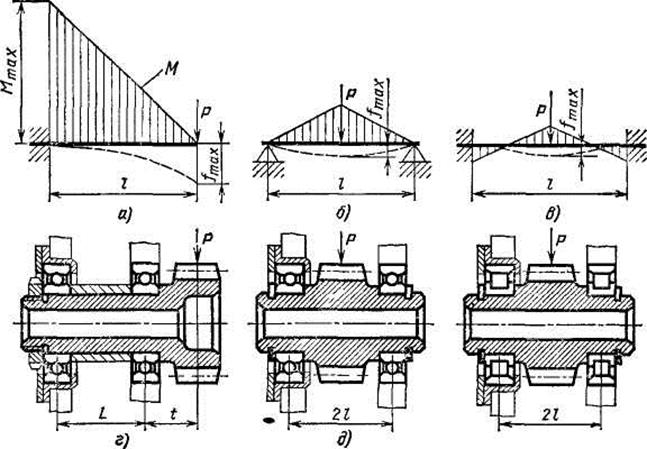 Рис. 5.3.8. Схемы нагружения:
Рис. 5.3.8. Схемы нагружения:
а) 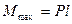 ;
; 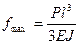 ; б)
; б) 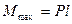 /4;
/4; 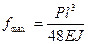 ; в)
; в) 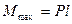 /8;
/8; 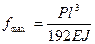 .
.
Нагрузка на подшипники двухопорного вала меньше нагрузки на передний подшипник консольного вала Р (1 + l/L) в 2 (1 + l/L) раза.
Еще благоприятнее соотношения для двухопорного вала с заделанными концами. Реальное приближение к этому случаю можно получить увеличением жесткости опор, например применением роликовых подшипников и усилением стенок корпуса
(рис. 5.3.8 , е). В данном случае максимальный изгибающий момент меньше в 4 раза по сравнению с консолью и в 2 раза по сравнению с двухопорным валом, установленным на шариковых подшипниках. Максимальный прогиб вала на жестких опорах соответственно меньше в 8 и 4 раза (без учета различия величин J и J').
Однако при коротких и жестких валах повышение жесткости опор практически не дает выгоды, так как жесткость вала стирает разницу между схемами валов свободно опертого и с заделанными концами.
Дата добавления: 2020-08-31; просмотров: 1664;











