Диффузия в твердых телах
При комнатной температуре диффузия в твердых телах обычно не проявляется. Тончайшее покрытие одного металла другим сохраняется длительное время практически неизмененным. Однако при температуре в несколько сот градусов покрытия уже не сохраняются: вследствие диффузии атомы покрытия проникают с заметной скоростью в глубь подложки. Это обстоятельство используется, например, в полупроводниковой технике для введения в полупроводник легирующих примесей при температуре в несколько сотен градусов по Цельсию.
Механизм диффузионных процессов в твердых телах можно понять, если использовать наши сведения о кристаллической структуре твердых тел. В равновесии атомы твердого тела совершают тепловые колебания около узлов кристаллической решетки. В идеальной структуре твердого тела все узлы решетки совершенно равнозначны и процесс диффузии происходить не может. Однако в реальном кристалле при заданной температуре существует некоторое число термических дефектов — нарушений кристаллической решетки. Впервые гипотеза о термических дефектах, согласно которой в результате тепловых флуктуации некоторые ионы могут покидать свои нормальные места в решетке и переходить в положения между другими узлами (межузлия), была предложена Френкелем. Впоследствии Шоттки предположил также, что в ионных кристаллах равное число катионов и анионов может уходить со своих нормальных мест в решетке, создавая катионные и анионные вакансии. Примером систем с преобладанием дефектов по Френкелю могут служить некоторые галогениды серебра (АgС1, АgВг). В кристаллах галогенидов щелочных металлов термические дефекты принадлежат к типу дефектов по Шоттки.
При повышении температуры кристалла возрастают равновесные концентрации вакансий и межузельных атомов, а при понижении температуры часть дефектов исчезает на стоках. Роль таких стоков могут играть другие дефекты решетки, в частности дислокации.
Если исходить из таких представлений о дефекте структуры кристаллической решетки, то становится понятным механизм диффузии и твердом теле. Пусть в соседстве с атомом, расположенным в узле решетки, расположен вакантный узел (дырка). Тогда колебательное движение атомов может приводить к перескоку атомаиз узла решетки в вакантный узел по «вакансионному механизму диффузии». В отсутствие внешних сил процесс диффузии является чисто релаксационным процессом, и определять его будет неравновесная характеристика образца, — например, градиент концентрации данного вещества или градиент температур.
Перескок атома в решетке определяется вероятностью нахождения дырки в окрестности данного атома, а также вероятностью преодоления атомом потенциального барьера, разделяющего начальное и конечное состояния атома. В более, усложненной модели Раиса кроме указанных вероятностей учитывается еще вероятность того, что в результате хаотического теплового движения другие атомы могут «помешать» перескоку, случайно увеличивая эффективную величину потенциального барьера.
Каждой температуре Т соответствует определенное равновесное число дырок:
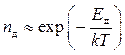 ,
,
где Ед — энергия, требуемая для образования одной дырки.
При всех температурах ниже точки плавления равновесное число дырок много меньше числа узлов N в кристаллической решетке, т.е.
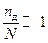 ,
,
 Рис. 4‑1 Энергетический барьер для движения нона в кристалле, находящемся в электрическом поле Е (вектор Е направлен по оси х).
Рис. 4‑1 Энергетический барьер для движения нона в кристалле, находящемся в электрическом поле Е (вектор Е направлен по оси х).
|
и корреляциями между положениями дырок можно пренебречь. Поэтому дырки можно рассматривать как «разреженный газ». Поскольку всякий перескок атома связан с перескоком в обратном направлении дырки, формально можно следить за потоком дырок и лишь из конечных результатов сделать вывод о поведении потока атомов.
Рассмотрим случай, когда на кристалл действует внешняя сила, а именно рассмотрим ионный кристалл в электрическом поле, напряженности 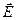 . Величина энергетического барьера U0 для перескоков иона (для простоты будем рассматривать движение ионов только одного вида, например катионов) в направлении поля уменьшится, а для перескоков в противоположном направлении соответственно увеличится на 1/2 qaE, где q — заряд иона, a — расстояние, на которое перемещается ион при одном перескоке (Рис. 4‑1). Таким, образом, вероятность перескоков иона в единицу времени в направлении поля увеличится в
. Величина энергетического барьера U0 для перескоков иона (для простоты будем рассматривать движение ионов только одного вида, например катионов) в направлении поля уменьшится, а для перескоков в противоположном направлении соответственно увеличится на 1/2 qaE, где q — заряд иона, a — расстояние, на которое перемещается ион при одном перескоке (Рис. 4‑1). Таким, образом, вероятность перескоков иона в единицу времени в направлении поля увеличится в  раз, а в направлении против поля — уменьшится во столько же раз. Это приведет к дрейфу анионов в направлении поля, т.е. к электропроводности, которая в данном случае есть просто вынужденная диффузия.
раз, а в направлении против поля — уменьшится во столько же раз. Это приведет к дрейфу анионов в направлении поля, т.е. к электропроводности, которая в данном случае есть просто вынужденная диффузия.
Связь между ионной электропроводностью σ и коэффициентом диффузии дается соотношением Эйнштейна:
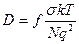 ,
,
где f — поправочный множитель;
N —концентрация ионов.
Соотношение можно понять следующим образом. При наложении электрического поля Е и наличия градиента концентрации ионов в кристалле возникает ток плотности
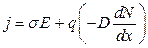 ,
,
 ,
,
где σ — удельная электропроводность;
Bи — подвижность ионов.
При статистическом равновесии полный ток равен нулю, т.е. ток поля ( 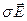 ) уравновешивается диффузионным током (
) уравновешивается диффузионным током ( 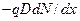 ). Поскольку
). Поскольку
 ,
,
где U — потенциал электрическогополя, при равновесии
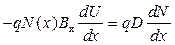 .
.
Интегрируя уравнение , получаем
 ,
,
где
 .
.
С другой стороны, в условиях равновесия концентрация ионов в электрическом поле должна подчиняться больцмановскому распределению
 .
.
Из сравнения выражений следует:
 .
.
Однако в ионных кристаллах мы сталкиваемся с отступлением от простого соотношения между коэффициентом диффузии и удельной электропроводностью. Именно поэтому в соотношении содержится поправочный множитель f. Наличие его легко понять. Так, при диффузии путем замещения вакансий подвижность, вычисленная из электропроводности, определяется подвижностью вакансий, а коэффициент диффузии меченого атома зависит от корреляции скачков атома. Очевидно, что после того как ион занял положение вакансии, вероятность скачка вперед и назад неодинакова: перескок меченого атома в прежнее положение при соседстве вакансии, занявшей место меченого атома, вероятней всякого другого перехода. В этом случае следует вводить множитель f как фактор корреляции последовательных перескоков. Вычисление фактора корреляции можно найти в оригинальных работах.
Поправочный множитель в может зависеть и от механизма диффузии.
Дата добавления: 2020-02-05; просмотров: 731;











