Уравнения переноса в физико-химической кинетике

В физико-химической кинетике часто приходится иметь дело с системами, состояние которых изменяется со временем случайным образом. Простейшим примером таких систем являются молекулы пли взвешенные частицы, находящиеся в тепловом движении. Это тепловое движение приводит к диффузии частиц, которая во многих случаях определяет ход химической реакции не только в газовой среде, но и в жидкостях и твердых телах. Поэтому вновь вернемся к феноменологической теории диффузии и прежде всего получим уравнение диффузии и его решения для некоторых важных случаев.[ii]

Уравнение диффузии

4.1.1. Как мы уже отмечали, диффузией называется процесс переноса вещества из одной части системы в другую, вызванный тепловым движением молекул. Мы видели, феноменологическая теория диффузии основана на законе Фика, устанавливающим связь между градиентом концентрации и потоком диффузии, который для удобства обозначений запишем в виде:

,

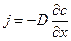где j — поток диффузии, т.е. количества вещества, проходящего за единицу времени через единицу площади поперечного сечения;
D — коэффициент диффузии;
c — концентрация;
х — координата в направлении нормали к поперечному сечению.

Коэффициент диффузии может зависеть, вообще говоря, как от координаты, так и от концентрации и имеет размерность (длина²/время). Во многих случаях коэффициент диффузии можно считать не зависящим от концентрации. Знак минус в уравнении показывает, что вещество диффундирует в обратном направлении по отношению к направлению роста концентрации.

Если на диффундирующие частицы действует какая-либо внешняя сила F (например, сила тяжести), направленная вдоль оси х, то частицы под ее влиянием будут двигаться со средней скоростью v == ВF (В — подвижность частиц). В этих условиях к потоку диффузии 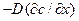добавится поток частиц под действием внешней силы и полный поток будет равен

.

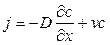Чтобы установить связь между коэффициентом диффузии D в подвижностью частиц B, рассмотрим стационарный случай (концентрация частиц не зависит от времени) при условии, что полный поток частиц равен нулю. Положим, что сила направлена в сторону уменьшающихся значений х, и обозначим ее 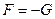. Решение уравнения дает:

.

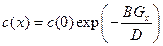Соотношение должно совпадать с формулой Больпмана для распределения частиц в поле силы:

,

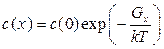где k — постоянная Больцмана;
Т — абсолютная температура.

Выражения и равны, если

, т.е. .

Таким образом, уравнение позволяет определить коэффициент диффузии частиц по их подвижности.

Подвижность сферической частицы в жидкости определяется хорошо известным законом Стокса.

,

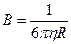где η — вязкость среды;
R — радиус частицы.

4.1.2. Уравнения и позволяют рассматривать лишь стационарные процессы диффузии, при которых концентрация и поток j не зависят от времени. Чтобы получить уравнение диффузии, дающее возможность рассматривать также и нестационарные процессы диффузии, используем соотношение

,

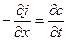которое показывает, что увеличение числа частиц на единичном интервале длины за единицу времени дс/дt равно разности между числом вошедших в этот интервал и вышедших из него частиц, — дj/дх. Подставив в уравнение величину j из , получим

.

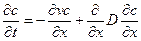При решении этого уравнения должны быть учтены начальные и граничные условия, соответствующие рассматриваемой задаче.

Решение такого уравнения, описывающего диффузию частиц, находящихся в начальный момент времени t = 0 в точке х = 0 ( ), имеет вид

,
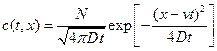где N — общее количество вещества.

Это решение представляет собой функцию нормального распределения относительно точки, движущейся в положительном направлении оси абсцисс со скоростью v. Ширина распределения может быть охарактеризована средним значением .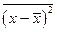

Среднее значение какой-либо функции по совокупности частиц с заданной зависимостью концентрации от координаты определяется соотношением

.

Легко показать, что

.

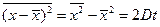Если в момент времени t=0 вещество не сосредоточено в одной точке, как полагали выше, а распределено определенным образом по х, то решение задачи о диффузии будет иметь вид

,

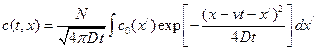где c₀(x) — начальная концентрация как функция координаты.

Положим теперь, что диффузия вещества происходит в какой-либо конечной области пространства. В этом случае следует указать, какие условия в соответствии с физической постановкой задачи нужно наложить на концентрацию или ее производные на границах данной области. Пусть, например, эта область ограничена поверхностью (например, стенкой сосуда), отражающей попадающие на нее частицы. На этой поверхности поток j должен равняться 0, т.е.

.

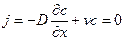Возможно, однако, существование и такой поверхности, которая захватывает все коснувшиеся ее частицы и прочно удерживает их. Для такой поверхности должно быть поставлено граничное условие

,

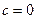свидетельствующее о том, что на ней нет способных к диффузии частиц.

В ряде диффузионных задач диффузионный поток на границе пропорционален концентрации частиц[17]:

.

Как оказалось, уравнения типа применимы не только для рассмотрения процессов диффузии, но и для решения некоторых задач физико-химической кинетики. Эти уравнения описывают большое число процессов, называемых марковскими.

Марковские процессы. Уравнение Фоккера — Планка.

Опишем состояние системы совокупностью переменных случайных величин 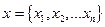. В частном случае, как мы уже говорили, под системой можно подразумевать броуновскую частицу или молекулу, а под х — ее координату, скорость, а также случайный заряд частицы или размер маленькой капли, которая случайным образом растет или испаряется в атмосфере своего пара и т.п. Пусть переменная х с течением времени последовательно принимает различные значения. Если эти последовательные значения х вообще не связаны друг с другом, т. е. не коррелируют, то процесс называют чисто стохастическим. Примером может служить последовательность появления разных сторон при выбрасывании монеты.

В более сложных случаях наблюдается корреляция между двумя последовательными событиями. Это — так называемый марковский процесс (по имени известного русского математика А.А. Маркова). Для этого процесса вероятность того или иного состояния в будущий момент времени зависит только от состояния в данный момент времени и не зависит от того, какие состояния система имела в прошлом. Примером марковского процесса может служить броуновское движение частиц; если мы знаем координату частицы, взвешенной в жидкости, в момент времени t₀, то можем предсказать вероятность ее местопребывания в определенной точке пространства в любой последующий момент времени.

Пример иного рода мы будем иметь, если рассмотрим процесс поглощения пара частицей сорбента при ее случайном движении в объеме с переменной концентрацией пара. Скорость поглощения пара зависит не только от количества сорбированного пара и его концентрации, но и от распределения поглощенного вещества по объему частицы, которое зависит от траектории движения частицы в предшествующие моменты времени.

Пусть 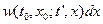обозначает марковскую вероятность перехода системы (частицы) из состояния (точки) x₀ в момент времени t₀ в интервал состояний x до x+dx к моменту времени t' > t₀ . Такой переход может быть совершен различными способами. Разбивая интервал времени на две части и интегрируя по всем положениям частицы в момент t, легко убедиться, что вероятность перехода 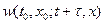удовлетворяет интегральному уравнению Смолуховского:

.

Действительно, вероятность перехода за время 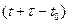из состояния x₀ в состояния, лежащие в интервале 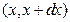равна сумме произведений вероятностей перехода за промежуток времени 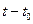в любое состояние 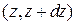и из него за промежуток времени τ в состояния, лежащие в интервале (х, х + dх).

Покажем теперь, что для некоторых случайных процессов интегральное уравнение Смолуховского сводится к дифференциальному уравнению. Если помножить выражение на произвольную функцию , которая вместе со своей производной обращается в нуль на концах изучаемого интервала, и проинтегрировать по всей области изменения х,то получим

.

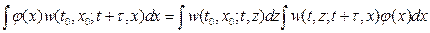Разложение по степеням (х—z) дает

,

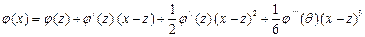где θ лежит между x и z.

Подставив это разложение в правую часть уравнения , перенеся первый член справа в левую часть уравнения и разделив обе части уравнения на τ (поскольку 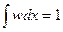), получим

.

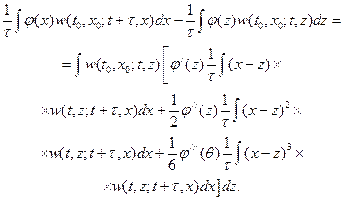Предположим, что для рассматриваемого процесса существуют пределы

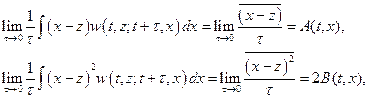
где А — средняя скорость процесса;
В — коэффициент, характеризующий случайные изменения переменной х.

Кроме того, предположим, что

.

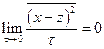т.е. будем считать, что вероятность больших отклонений за малое время достаточно быстро стремится к нулю. Проинтегрируем уравнение по частям и перейдем к пределу при . Тогда, в силу условий, наложенных на φ, получим

.

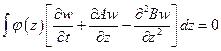Поскольку уравнение справедливо для произвольной функции 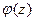, подынтегральная функция должна обращаться в нуль. Окончательное уравнение для вероятности w имеет вид

.

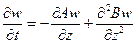где z — параметр, определяющий состояние системы (координаты частиц).

Полученное уравнение носит название уравнения Фоккера — Планка или Эйнштейна — Фоккера. Это уравнение может быть распространено на систему со многими переменными.

Уравнения диффузии и Фоккера —Планка равнозначны, если рассматривается диффузия невзаимодействующих частиц, т.е. коэффициент диффузии не зависит от концентрации. В этом случае переход от вероятности w к концентрации с осуществляется умножением на полное число частиц. Следует обратить, однако, внимание на различную форму записи уравнения диффузии и уравнения Фоккера — Планка . Уравнение Фоккера — Планка можно переписать в виде

.

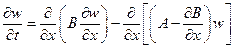Из уравнения и видно, что В имеет смысл коэффициента диффузии. Средняя скорость смещения А состоит из двух слагаемых

,

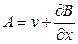одно из которых (v) является средней скоростью смещения под действием внешних сил, второе (dB/dx) связано с неоднородностью среды, в которой происходит диффузия.