Задача о достижении границы
Задача о вероятности достижения границ блуждающей частицей может быть решена на основании уравнения Фоккера — Планка. При этом, если частица, достигающая границ интересующей нас области, теряет способность к дальнейшему блужданию, концентрация с или соответственно вероятность w на границах области должны обращаться в нуль.
Однако возможен и второй путь решения этой задачи. Он заключается в решении уравнения для вероятности хотя бы одного достижения границ за время t. Рассмотрим одномерное движение частицы. Обозначим через W(х, t) вероятность того, что частица, находящаяся в момент времени t == 0 в точке х (а < х < b), за время t хотя бы раз достигнет границ области х == а или х = b. Через  обозначим вероятность перехода частицы за время t из точки х в интервал
обозначим вероятность перехода частицы за время t из точки х в интервал 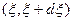 , предполагая при этом, что она не коснется границы области а или b. Вероятность того, что частица, находящаяся при t == 0 в точке х, будет находиться к моменту времени t в какой-либо точке между а и b, ни разу не коснувшись границ, будет равна
, предполагая при этом, что она не коснется границы области а или b. Вероятность того, что частица, находящаяся при t == 0 в точке х, будет находиться к моменту времени t в какой-либо точке между а и b, ни разу не коснувшись границ, будет равна
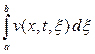 .
.
Кроме того, она равна 1 — W(x, t). Таким образом
 .
.
Для функции W(x, t) может быть записано интегральное уравнение по аналогии с уравнением Смолуховского для вероятности перехода w:
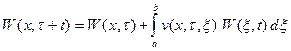 .
.
Действительно, вероятность W(x,τ+t) того, что за время τ+t произойдет хотя бы одно достижение границы, равно сумме вероятности W(x,t) хотя бы одного достижения границы за время τ и вероятности того, что за время τ достижения границы не произойдет, а оно произойдет за остальной промежуток времени t. Граничными условиями при х = а и х = b будут
 ,
,
поскольку уже при t = 0 граница достигнута. Для всех значений х внутри интервала (a, b) при t = 0 вероятность W(x,t), очевидно, равна нулю, т.е.
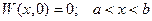 .
.
Так как v (х,τ,ξ) обозначает вероятность перехода частицыиз точки х в точку ξ за время t при условии отсутствия касания границ, а w(х,τ,ξ) — вероятность того же перехода без каких-либо дополнительных условий, ясно, что v (х,τ,ξ) < w (х,τ,ξ).
Если интервал времени τ стремится к нулю, то вероятность достижения границы за это время также будет стремиться к нулюдля всех точек х в интервале от a до b. Следовательно, при  v(х,τ,ξ) стремится к w (х,τ,ξ). Поэтому полагаем, что
v(х,τ,ξ) стремится к w (х,τ,ξ). Поэтому полагаем, что
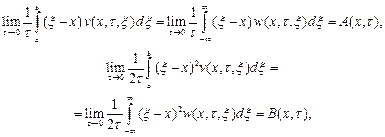
где A и B — коэффициенты, введенные в предыдущем параграфе.
Поскольку мы рассматриваем случайное движение в координатном пространстве, величина B имеет смысл коэффициента диффузии, т. е. B == D. Заметим также, что если для функции w выполняется условие ,то аналогичное условие будет иметь место и для v:
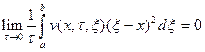 .
.
Кроме того
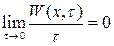 .
.
Поэтому при  из выражения имеем
из выражения имеем
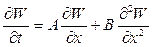 .
.
Это дифференциальное уравнение получено для вероятности хотя бы одного достижения границы за время t частицей, которая при t= 0 находилась в точке х. Граничными условиями его будут условия . Далее, для всех внутренних точек в интервале от a до b вероятность достижения границы за время t=0 равна нулю, т. е. начальные условия имеют вид
 .
.
Все полученные в этом параграфе уравнения, несмотря на то что говорится лишь о координате частицы, справедливы для любого случайного параметра, определяющего состояние системы. Уравнение может быть обобщено для системы со многими переменными. Если найдена вероятность W, то распределение частиц по времени пребывания в области (a, b) до достижения границы дается величиной  . Следует иметь в виду, что решение уравнений Фоккера— Планка или уравнения часто оказывается весьма сложным. Поэтому в ряде случаев вместо вероятности W, имеющей смысл функции распределения по времени пребывания частицы в области, приходится ограничиваться несколькими первыми моментами этого распределения.
. Следует иметь в виду, что решение уравнений Фоккера— Планка или уравнения часто оказывается весьма сложным. Поэтому в ряде случаев вместо вероятности W, имеющей смысл функции распределения по времени пребывания частицы в области, приходится ограничиваться несколькими первыми моментами этого распределения.
Дата добавления: 2020-02-05; просмотров: 663;











