Теория передачи импульса.

Основная цель проводимого ниже анализа диффузии ионов в газе в рамках теории передачи импульса при столкновении частиц состоит в том, чтобы показать, как простыми физически наглядными средствами можно получить зависимость сечения рассеяния σ_d согласно уравнению . К тому же мы увидим, что результаты для подвижности ионов при использовании приближения свободного пробега и импульсного приближения практически совпадают. Подобная аналогия не имеет, однако, общего характера и связана с тем, что рассматриваются лишь следы примеси ионов к газу. Для произвольной смеси газов соответствующие результаты оказываются различными, по крайней мере в первом приближении. Анализ подвижности ионов в смеси нескольких газов проводится особенно просто в рамках теории передачи импульса и также здесь затрагивается.

Представления о свободном пробеге частиц между столкновениями были сформулированы еще Максвеллом. Интересно отметить, что Максвелл первым подошел к описанию диффузии как процесса, связанного с передачей импульса между частицами при столкновении, но не сумел преодолеть возникшие трудности (из-за ошибки, которая была исправлена Клаузиусом). Последняя теория была независимо раз-вита Стефаном и позднее использована Ланжевеном при создании первой математически строгой теории подвижности ионов при слабых электрических полях. После этого никто, явно, не вспоминал об этой теории в течение многих лет, пока она не была открыта еще раз (по-видимому, тоже независимо) Френкелем и Презентом и де-Бетаном. Одним из стимулов для ее воссоздания явилась проблема разделения изотопов, вставшая в годы второй мировой войны.

Особенно просто представление об обмене импульсами при столкновении частиц объясняет подвижность ионов в газе. Из второго закона Ньютона следует, что электрическое поле передает импульс ионам, но поскольку последние в среднем не ускоряются, этот импульс должен быть передан молекулам, с которыми ионы сталкиваются. За одно столкновение от иона к молекуле газа передается импульс, компонента которого вдоль направления относительной скорости v_r имеет вид

.

Если теперь усреднить это выражение по многим столкновениям, то следует ожидать в среднем обращения в нуль всех случайных компонент движения и рассматривать вклад только от дрейфовой скорости иона. Отсюда получаем, что за одно столкновение молекуле газа передается импульс, в среднем равный 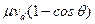. Среднее число столкновений, которые ион испытывает в единицу времени в единице объема, когда прицельное расстояние находится в интервале междуρ и ρ + dρ, равно

.

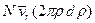Таким образом, полный импульс, переданный от иона газу и равный еЕ, имеет вид

.

С точностью до множителя ξ порядка единицы выражение совпадает с формулами и в теории свободного пробега, причем сечение рассеяния определяется соотношением

.

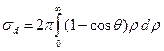Посколькумы стремились найти только вид сечения σ_d, проведенное выше достаточно грубое усреднение передаваемого импульса по столкновениям можно считать приемлемым; заметим, однако, что более строгий подход позволяет также определять и правильную численную величину множителя ξ.

Полученные выше соотношения можно использовать для дальнейшего построения теории рассматриваемого явления, но их вывод, очевидно, не отличается существенно от выводов теории свободного пробега и здесь может быть опущен. Только что описанный подход, однако, настолько непосредственно можно обобщить на случай ионов в многокомпонентных смесях газов, что провести это обобщение лучше всего сейчас. При учете только парных столкновений частиц полный импульс, переданный ионом в единицу времени газу в единице объема, является просто суммой импульсов, переданных ионом молекулам каждого сорта, так что обобщение выражения на случай смеси газов приводит к уравнению

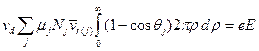
или, в более подробной записи,

.

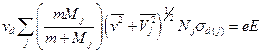Полученный результат справедлив при любой напряженности электрического поля. В расчетах мы вполне можем пренебрегать численным множителем ξ, поскольку в окончательном виде результаты будут выражены через скорости дрейфа ионов в чистых газах. В пределе слабого внешнего поля энергия движения ионов целиком определяется тепловым движением и

,

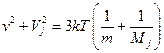так что из уравнения следует

.

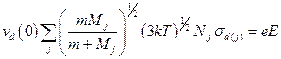Каждый член написанной суммы определяет скорость 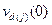дрейфа иона в чистом газе молекул j-го сорта с плотностью N, равной суммарной плотности числа частиц смеси:

,

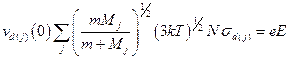используя это уравнение, приведем к виду

,

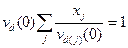где 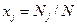называется мольной долей частиц j-го сорта в смеси газов.

Удобнее переписать последнее уравнение в другой форме

или, вводя подвижность ионов,

.

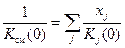Последний результат известен как закон Бланка.

При анализе движения ионов в сильном внешнем поле встает проблема определения вклада в среднюю энергию движения ионов от энергии дрейфового движения и случайной компоненты энергии, обусловленной электрическим полем. Задача решаемая, но мы ее рассматривать в данном курсе лекций не будем.