Теория слабого поля

Ввиду того что при слабых полях, наложенных на плазму, выполняется соотношение Эйнштейна, теория подвижности ионов в этих условиях вполне эквивалентна классической кинетической теории диффузии. Впервые строгая формулировка кинетической теории газов была дана во второй половине XIX в. в работах Максвелла и Больцмана, однако им не удалось преодолеть множества математических проблем, связанных с расчетом явлений переноса в газовой среде. Первые решения макроскопических уравнений переноса в 20-е годы нашего века независимо получили два исследователя — Чепмен, который исходил из максвелловского уравнения переноса частиц, и Энског, исходивший из больцмановского уравнения для функции распределения частиц. Здесь мы очень кратко, схематично изложим метод Чепмена—Энскога решения интегро-дифференциального кинетического уравнения.

Все явления переноса в газе возникают из-за отклонений функции распределения частиц от равновесной (максвелловской). Поэтому основная проблема строгой кинетической теории заключается в отыскании неравновесной функции распределения, из которой путем интегрирования находят потоки различных величин. Например, диффузионный поток определяется интегралом от произведения скорости молекулы на функцию распределения частиц. Сравнение этого выражения с феноменологическим уравнением, определяющим коэффициент диффузии (см. ) позволяет выразить D через параметры, характеризующие процессы столкновения частиц.

Функцию распределения частиц находят из решения уравнения Больцмана, имеющего вид уравнения непрерывности. При описании движения ионов в смеси газов больцмановское уравнение записывают в следующей форме:

,

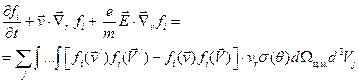где выражение в правой части определяет изменение числа ионов благодаря столкновениям с частицами сорта j[16]. Суммирование распространяется на все нейтральные молекулы в смеси газов; поскольку мы предполагаем наличие только исчезающе малого количества ионов в среде, никакого члена, ответственного за взаимные столкновения ионов между собой, в уравнении нет. Значки штрихов отмечают скорости частиц после столкновений. Используемые функции распределения нормированы на величину плотности числа частиц, так что

,

.

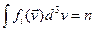Если найдено решение уравнения , то вычисление скорости дрейфа ионов проводится непосредственно

.

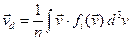При слабом внешнем поле средняя энергия ионов связана с температурой среды соотношением

,

которое учитывает, что энергия дрейфового движения пренебрежимо мала по сравнению с тепловой.

При выводе кинетического уравнения Больцмана предполагают, что на функцию распределения влияют только парные соударения частиц. Кроме того, запись правой части этого уравнения в формеотвечает учету только упругих столкновений.

Дальнейшие выкладки очень сложны. В итоге первое приближение дает следующую зависимость для коэффициента диффузии:

.

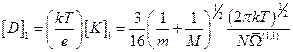Полученное соотношение аналогично результату в теории свободного пробега, поскольку 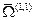представляет собой взвешенное среднее транспортное сечение рассеяния σ⁽¹⁾, которое в точности совпадает с σ_d.

Подводя итог, отметим, что эти результаты справедливы только в предельном случае нулевого электрического поля, когда полностью пренебрегают влиянием остальных частиц газа на процесс столкновения двух частиц, учитывают только упругие столкновения и считают отклонения от равновесия настолько малыми, что поток ионов линеен относительно градиента плотности числа частиц и напряженности электрического поля. Как уже отмечалось ранее, эти результаты верны в случае как квантовой, так и классической механики, но при условии, что кинетическое уравнение Больцмана справедливо.