Распределение частиц по скоростям в неравновесном газе
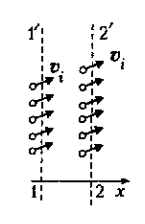 Рис. 1‑4 Рис. 1‑4
|
1.3.1.В неравновесном пространственно неоднородном газе максвел-ловское распределение по скоростям с очевидностью нарушается. В самом деле, это распределение изотропно. Оно утверждает, что в газе в любом направлении движется в среднем одно и то же число частиц с одними и теми же средними характеристиками. Но существование диффузионных потоков показывает, что в пространственно неоднородных состояниях в одну сторону либо движется больше частиц, чем в другую, либо они переносят с собой большую энергию, либо больший средний импульс.
Нетрудно понять, по какой причине возникают отклонения от максвелловского распределения. Рассмотрим группу частиц, движущихся с одинаковыми скоростями вблизи значения 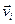 и предположим, что мы тем или иным способом сделали плотность их числа, ni меняющейся вдоль оси х. Тогда число частиц этой группы, Ni, заключенных в элементе объема V между двумя бесконечно близкими плоскостями. 11' и 22', перпендикулярными к оси х (Рис. 1‑4), начнет меняться[3].
и предположим, что мы тем или иным способом сделали плотность их числа, ni меняющейся вдоль оси х. Тогда число частиц этой группы, Ni, заключенных в элементе объема V между двумя бесконечно близкими плоскостями. 11' и 22', перпендикулярными к оси х (Рис. 1‑4), начнет меняться[3].
В самом деле, поток частиц, втекающих в объем через сечение 11', связан с плотностью их числа, 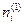 в точке 1:
в точке 1:

а вытекающих через сечение 22' — с плотностью 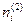 в точке 2:
в точке 2:
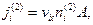
здесь A — площадь обоих сечений.
Так как 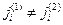 , втекать в объем V и вытекать из него будет разное число частиц. И разница
, втекать в объем V и вытекать из него будет разное число частиц. И разница 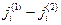 определит скорость
определит скорость 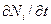 возрастания числа частиц Ni в этом объеме (если
возрастания числа частиц Ni в этом объеме (если 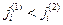 то «возрастание» будет отрицательным).
то «возрастание» будет отрицательным).
Представляя 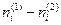 в виде
в виде 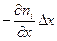 , где
, где 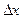 — расстояние между плоскостями, и учитывая, что V =АΔх, получим
— расстояние между плоскостями, и учитывая, что V =АΔх, получим
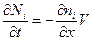 .
.
Мы пишем здесь круглые значки дифференциалов, потому что Ni и ni зависят от двух переменных, х и t, и мы дифференцируем каждый раз по одной из них.
1.3.2.Ясно, однако, что никакие изменения чисел Ni, не могут продолжаться до бесконечности. Им будут противодействовать те процессы, которые в изолированном газе обеспечивают установление максвелловского распределения. Эти процессы связаны со случайными столкновениями молекул рассматриваемой i-й группы с другими молекулами (в том числе и других сортов) находящимися в пределах объема V (между собой молекулы i-й группы не сталкиваются, ибо движутся с одной и той же скоростью vi).
Непосредственно после столкновения молекула не покидает объема V, она остается внутри него. Но ее скорость меняется, она получает другие значения, отличные от vi. Поэтому после столкновения молекула пополнит состав какой-то другой скоростной группы, а число молекул i-й группы уменьшится на единицу.
Число столкновений, которые молекула i-й группы испытывает в единицу времени, равно обратной величине времени ее свободного пробега, τi. Поэтому скорость их убывания из-за столкновений
 .
.
Индекс i у времени τi показывает, что оно может зависеть от скорости частиц, vi.
Конечно, место выбывших молекул (выбывших не из объема V, а из i-й группы) будут занимать молекулы других скоростных групп (но того же сорта), находящихся в объеме v и случайно получивших после соударения нужную скорость вблизи vi,. Вычислить число прибывающих таким способом в i-ю группу молекул гораздо сложнее. Его грубую оценку можно получить из следующих соображений.
Ясно, что в равновесных условиях число прибывающих молекул должно в точности компенсировать убыль, определяемую формулой . Поэтому, обозначая равновесные величины верхним индексом нуль, можно записать
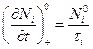 .
.
В правой части этого выражения стоят величины, относящиеся к частицам i-й группы. Но, в действительности, скорость  определяется столкновениями, в которых участвуют все частицы данного сорта, находящиеся в пределах объема V: любая из них может получить в результате столкновения нужную скорость и оказаться в i-й группе. Поэтому можно ожидать, что величина
определяется столкновениями, в которых участвуют все частицы данного сорта, находящиеся в пределах объема V: любая из них может получить в результате столкновения нужную скорость и оказаться в i-й группе. Поэтому можно ожидать, что величина  не будет слишком меняться при таких отклонениях от равновесия, когда полное число частиц в объеме V остается неизменным, и они только чуть иначе распределяются по скоростям.
не будет слишком меняться при таких отклонениях от равновесия, когда полное число частиц в объеме V остается неизменным, и они только чуть иначе распределяются по скоростям.
Значит, мы можем записать приближенно, что и в неравновесных условиях
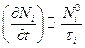 .
.
Полная же скорость возрастания чисел Ni вследствие столкновений получится вычитанием из :

(если Ni > N0, то «возрастание» будет отрицательным).
Физический смысл этого соотношения станет яснее, если, воспользовавшись тем, что Ni0 — постоянная величина, переписать его в виде
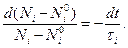
Отсюда следует, что
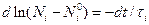 ,
,
т.е.
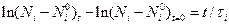
или
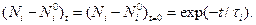
 Рис. 1‑5
Рис. 1‑5
|
Эта зависимость показана на Рис. 1‑5 для случая, когда 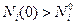 . Видно, что в результате столкновений начальное отклонение от равновесности, чем бы оно ни было вызвано, затухает по экспоненте за время ~ τi , если нет никаких причин, которые это отклонение поддерживали бы. Таким образом, время свободного пробега τi, играет роль микроскопического "времени памяти". В этом качестве его называют микроскопическим временем релаксации.
. Видно, что в результате столкновений начальное отклонение от равновесности, чем бы оно ни было вызвано, затухает по экспоненте за время ~ τi , если нет никаких причин, которые это отклонение поддерживали бы. Таким образом, время свободного пробега τi, играет роль микроскопического "времени памяти". В этом качестве его называют микроскопическим временем релаксации.
1.3.3.Ясно, что всякие изменения чисел Ni прекратятся, когда сумма скоростей и обратится в нуль:

Это условие и определяет значения Ni, устанавливающиеся в стационарном состоянии. Из него, учитывая, что Ni /V = ni, для стационарной плотности числа частиц i-й группы получим
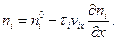
Так как второй член в правой части этого равенства при малых градиентах дает лишь небольшую поправку к максвелловской величине 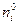 , можно без большой ошибки заменить в нем неизвестную величину ni, на максвелловское значение плотности числа частиц
, можно без большой ошибки заменить в нем неизвестную величину ni, на максвелловское значение плотности числа частиц 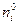 . Тогда окончательно
. Тогда окончательно
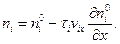
Наш анализ показывает, таким образом, что в пространственно неоднородном газе, когда  , распределение молекул по скоростям действительно становится анизотропным, не максвелловским, так что число частиц, движущихся со скоростями vix > 0, не равно числу частиц, имеющих такую же по величине, но противоположную по направлению скорость vix < 0. При этом полная плотность числа частиц в данной точке не меняется по сравнению с равновесной, поскольку увеличение числа первых компенсируется уменьшением числа вторых.
, распределение молекул по скоростям действительно становится анизотропным, не максвелловским, так что число частиц, движущихся со скоростями vix > 0, не равно числу частиц, имеющих такую же по величине, но противоположную по направлению скорость vix < 0. При этом полная плотность числа частиц в данной точке не меняется по сравнению с равновесной, поскольку увеличение числа первых компенсируется уменьшением числа вторых.
Отметим в заключение, что те рассуждения, которые привели нас к соотношению , довольно сильно огрубляют действительность. Поэтому в большинстве случаев уравнение , как показывает опыт, не годится для получения точных количественных результатов. Но оно всегда полезно для качественного анализа различных ситуаций.
Дата добавления: 2020-02-05; просмотров: 604;











