Диффузия и подвижность

Когда система находится во внешнем поле, на каждую частицу действует отличная от нуля сила F. Собственно говоря, одно внешнее поле такого типа присутствует всегда — это поле тяжести с 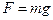. И если мы о нем не вспоминаем, это значит просто, что разные части системы находятся примерно на одной высоте. Для ионов в электролитах и электронов в металлах или полупроводниках таким полем может быть электрическое поле с F = еЕ, где e — заряд частицы, Е — напряженность поля.

Во всех таких случаях на случайное блуждание частицы накладывается ее направленный дрейф по полю, который приводит к возникновению потока частиц

,

где п и v_др — соответственно, плотность числа частиц и средняя скорость их дрейфа в некотором сечении сосуда площади А, перпендикулярного направлению скорости (и внешнего поля).

С помощью небольшой хитрости величину дрейфовой скорости можно найти, не вникая в детали движения частиц. Для этого нужно учесть, что в замкнутой системе направленный дрейф частиц данного сорта будет приводить к неоднородному их распределению в пространстве и вызывать, таким образом, диффузионный поток противоположного направления. Равновесие же наступит тогда, когда два этих потока, дрейфовый и диффузионный, станут равными по величине.

Поскольку все это происходит во внешнем поле, распределение частиц в пространстве будет определяться при этом формулой Больцмана: 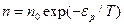из которой следует, что

,

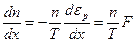где есть сила, действующая на частицу.

Приравнивая теперь дрейфовый поток диффузионному потоку 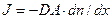и используя полученное выражение для dn/dx. получим:

.

Таким образом, под действием поля частица дрейфует с постоянной скоростью, пропорциональной действующей силе. Как если бы на нее помимо внешней силы действовала бы равная по величине и противоположная по направлению сила трения, пропорциональная скорости. Коэффициент пропорциональности между скоростью дрейфа и силой называют подвижностью. Из формулы видно, что между подвижностью, b, и коэффициентом диффузии, D, существует простая связь:

.

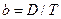Это соотношение, которое носит имя Эйнштейна, замечательно тем, что устанавливает связь между двумя совершенно различными по виду явлениями. Коэффициент диффузии характеризует случайное блуждание частиц, которое приводит, в частности к флуктуациям плотности. Подвижность же характеризует их регулярное движение под действием внешней силы. На первый взгляд это обычное механическое движение. Но оно сопровождается трением. В результате энергия этого упорядоченного движения, как говорят, диссипирует, т.е. превращается в энергию хаотического движения частиц.

Оказывается, таким образом, что диссипация энергии, а любой ее вид так и норовит перейти в тепло, тесно связана с наличием флуктуаций. Не было бы флуктуаций, исчезла бы и диссипация. Мир стал бы чисто механическим, в нем ничего бы не забывалось, и все было бы предопределено заранее. Данте приснилось, что тусклая надпись на воротах, ведущих в такой мир, кончается словами: «оставьте всякую надежду те, кто входит».

Задачи

Задача.

Оцените время, за которое газовая молекула доберется посредством диффузии от одного конца сосуда с линейными размерами порядка 10 см до другого.

Решение. Используя формулу и выбирая 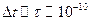с и 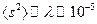см, получим с.

Задача.

2 Из формул , и следуют следующие простые соотношения: , , где 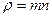— плотность газа. Пользуясь табличными данными, проверьте, насколько хорошо выполняются эти соотношения.

Задача.

В закрытой трубке, один конец которой поддерживается при температуре вдвое выше температуры второго конца, находится смесь легких и тяжелых молекул. Во сколько раз будет выше концентрация легких молекул у горячего конца?

Решение. Процесс термодиффузии будет продолжаться до тех пор, пока поток, определяемый формулой , не обратится в нуль. А для этого произведение 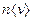должно перестать зависеть от х, или, иными словами — от температуры. Поскольку 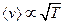, то в трубке установится распределение плотности числа легких частиц . А их концентрация, , будет меняться вдоль трубки как , поскольку 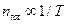. Таким образом, .

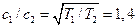Задача.

В условиях, когда нет конвекции, скорость испарения жидкости лимитируется скоростью диффузии ее паров. Учитывая это обстоятельство, оценить время, за которое испарится вода, заполняющая 1/3 стакана высотой l = 10 см. Стакан находится в помещении с относительной влажностью воздуха 70%. Плотность насыщенных паров воды при нормальных условиях 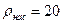г/м³.

Решение. Плотность числа молекул воды у поверхности жидкости, n_нас, определяется плотностью насыщенного пара. У верхнего же края стакана из-за конвективных потоков, "сдувающих" лишние молекулы воды, она будет определяться влажностью: n₀ = 0,7 n_нас.

Далее, в стационарных условиях, которые быстро установятся, поток молекул пара должен быть одинаков в любом сечении стакана. Поэтому будет постоянен и градиент плотности (Рис. 1‑10)

.

Таким образом, поток молекул воды в соответствии с равен

,

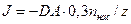где A — площадь сечения стакана (знак «-» означает, что поток направлен против оси z).

Этот поток определяет убыль числа молекул жидкости, N:

,

где n_B — плотность числа частиц в воде, V — объем жидкости. Приравнивая 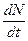и J, получаем уравнение

или

Рис. 1‑11

.

Интегрируя левую сторону по z в пределах до l, а правую —по t от 0 до t, получим

.

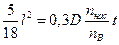Отсюда

.

Для оценки коэффициента диффузии паров воды в воздухе воспользуемся формулой , взяв характерные значения см и с. Получим D = 0,3 см²/с, что является типичной величиной для газов. Используя это значение D, найдем

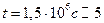месяцев.

Задача.

Датчик термопарного вакууметра использует для своей работы зависимость теплопроводности разреженного газа от давления. Он содержит нагреваемую током металлическую проволочку, температура которой определяется балансом между подводимой к проволочке мощностью и отводимым по газу теплом. Эта температура измеряется термопарным термометром, который служит, таким образом, индикатором давления. Оценить верхнюю границу давлений, которые можно хорошо измерять с помощью такого датчика, если характерный диаметр сосуда d, в котором он заключен, имеет порядок 1 см, а теплопроводность воздуха при нормальных условиях 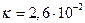Вт/К•м. Относительная молекулярная масса воздуха μ=29.

Решение. По формуле . Для двухатомного газа с_v = 5/2, а средний модуль скорости можно оценить из соотношения 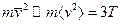, что дает см/с. Таким образом, для площади эффективного сечения получаем

.

Вакуумметр будет хорошо работать, когда длина свободного пробега . Отсюда получаем условие . Учитывая, что плотность частиц в газе при нормальных условиях см^-3 , получаем

.

Задача.

Стирающее память случайное воздействие жидкой среды на движение больших посторонних молекул можно представлять как действие обычной силы трения, обусловленной вязкостью. Время корреляции есть интервал времени, за который исчезает любое направленное движение молекул. Его можно оценить как время, за которое сила трения меняет средний импульс частицы на величину порядка его самого: . Оцените из этих соображений величину τ_c для молекулы молекулярной массы μ ~ 500 и линейными размерами 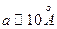, находящейся в воде. Вязкость воды η = 10^-2 г/см • с. Для оценки силы трения считайте, что в движение частицы вовлекаются слои жидкости, находящиеся от нее на расстояниях порядка ее радиуса, а более далекие остаются неподвижными.

Решение

В соответствии с формулой

.

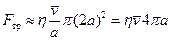Из условия 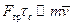получаем: 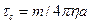. Подставляя числа, находим τ_с ~ 10^-13 с.

Задача.

При Т = 20°С проводимость 15% раствора КС1 в воде (15 г КС1 на 100 г раствора) σ = 0,2 Ом^-1см^-1. Считая подвижности ионов К⁺ и С1^- одинаковыми, оцените из этих данных величину их коэффициента диффузии в воде. Относительная молекулярная масса КС1 и μ = 74,5. Считайте, что удельный вес раствора близок к единице.

Решение. Под действием электрической силы еЕ, где е — заряд иона, E — напряженность электрического поля, ион получает дрейфовую скорость v_др = bеЕ, где b — подвижность. Это приводит к среднему потоку ионов каждого сорта 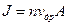, где n — плотность их числа, А — площадь сечения. Учитывая, что в величину электрического тока, I_e , дают вклад оба сорта ионов, получаем

.

С другой стороны, по определению проводимости, I_e = σEA. Отсюда σ = 2ne²b, т.е. b = σ/2ne², a D = bТ = σT/2ne². Считая, что m = 15 г КС1 заключено в 100 см³ раствора, оцениваем

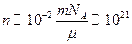см^-3.

При вычислении удобно выразить Т в электрон-вольтах: 1 эВ = 1,14•10⁴ К, а е² представить в виде е•1,5•10^-19 кулон. Тогда для D получится правильная размерность:

,

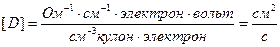так как

.

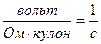Подставляя числа, получаем

см²/c.

Задача.

Состояние разомкнутого концентрационного элемента можно рассматривать как стационарное состояние, в котором диффузионный поток ионов NO₃^- , текущий через пористую перегородку вследствие разницы концентраций этих ионов в двух половинах сосуда, уравновешивается их дрейфовым потоком, возникающим под действием электрической силы еЕ. Пользуясь этими соображениями, вычислить величину ЭДС элемента.

Решение. Диффузионный ток в некотором сечении внутри перегородки

.

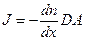Дрейфовый ток

.

Приравнивая эти токи, получаем

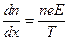
или

.

При интегрировании по толщине перегородки учтем, что есть работа по перемещению единичного заряда из одной половины сосуда в другую, т.е. величина ЭДС. Таким образом,

.

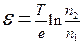2 Процессы переноса в применении к газам[i]