Диффузия как процесс случайного блуждания

1.5.1.Для описания процесса диффузии можно использовать совершенно другой подход, связанный с именами Эйнштейна и Смолуховского, который пригоден не только для газов, но и для жидкостей и твердых тел.

Рис. 1‑7

Пусть одна из частиц жидкости, твердого тела или газа, чем-то отличается от других, так что можно, хотя бы в принципе, следить за ее перемещениями. Реально это можно сделать, конечно, только если частица достаточно велика, как это имеет-место, например, в коллоидных взвесях, используемых для наблюдения броуновского движения. Но в принципе можно вести речь о любой частице, хоть как-то отличающейся от других.

Если отметить точками 0, 1, 2, 3, ... положение частицы через равные промежутки времени Δt, то получится картина, схематически изображенная на Рис. 1‑6. Стрелками на этом рисунке показаны перемещения частицы, , за последовательные интервалы времени [6]. А полное перемещение 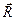будет иметь вид суммы:

Величина и направление перемещений , будут случайно меняться от наблюдения к наблюдению. Поэтому какие-то определенные суждения можно сделать только об их поведении в среднем. При этом процедура осреднения подразумевает, как всегда, проведение многократных измерений. Можно представить себе, например, что мы следим за перемещениями, , множества N идентичных частиц ( - номер частицы), помещенных в начальный момент в какую-то точку среды.

В однородной среде в отсутствии внешних полей направления «туда» и «обратно» равноправны. Поэтому числа частиц, переместившихся за один шаг вперед или назад, должны быть в среднем одинаковы. Это значит, что средние значения компонент векторов будут равны нулю. А вместе с ними будет равно нулю и среднее перемещение частицы за время t, . Но частицы будут при этом, конечно, расползаться в пространстве. Одни из них уйдут в одну сторону, другие — в другую, и средний квадрат их перемещения, , будет отличен от нуля.

Рис. 1‑8

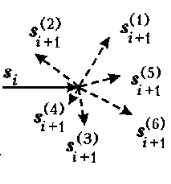
Чтобы понять, как он будет зависеть от времени наблюдения, выберем величину Δt не слишком малой. Тогда случайное воздействие среды на движение частицы приведет к тому, что ее последовательные перемещения 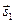, , ,... станут статистически независимыми. Это значит, что, если мы, проводя опыт с N частицами, отберем те N* из них, которые на i-м шаге переместились на одно и то же расстояние , мы увидим, что их перемещения 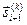( ) за следующий интервал времени будут совершенно произвольны в том смысле, что величина и направление этих перемещений никак не будут связаны с величиной и направлением (Рис. 1‑7).

В этом случае , поэтому

В стационарном состоянии, когда в среднем со временем ничего не меняется, все члены этой суммы одинаковы и равны просто среднему квадрату смещения частицы за время Δt, . А так как их число равно числу интервалов, t/Δt, в результате получаем:

.

В отличие от случая свободного движения, времени теперь пропорционален не сам путь, а его средний квадрат. Это фундаментальное следствие рассматриваемого подхода к описанию случайного движения частиц было экспериментально проверено Перреном на броуновских частицах.

1.5.2.Характерную величину интервала Δt, после которого стирается память о предыдущем движении, называют временем корреляции и обозначают τ_c. Его величина определяется конкретными свойствами среды.

Для частицы газа, например, это время будет опять порядка времени свободного пробега τ, величина которого ~ 10^-10 с. На меньших интервалах вероятность соударения будет невелика, и скорость частицы, а значит, и ее последующее перемещение, будут оставаться большей частью неизменными. Но уже одно гарантированное соударение полностью стирает память о предыдущем движении частицы ввиду случайности передаваемого ей импульса.

а) б) Рис. 1‑9

При этом существенно, впрочем, чтобы масса рассматриваемой частицы была меньше или порядка массы остальных молекул газа. Если же речь идет о тяжелой посторонней частице, находящейся в газе легких молекул, одного соударения будет недостаточно. Средняя энергия такой частицы, , где Π —ее импульс, а M — масса, будет равна средней энергии молекул газа, , где p и m — соответственно импульс и масса молекулы. Поэтому в среднем импульс частиц будет в раз больше импульса молекул, и нужно, грубо говоря, соударений, чтобы он существенно изменился. Это значит, что время корреляции будет примерно в раз больше времени свободного пробега частицы, τ, понимаемого как время между двумя последовательными соударениями.

Совсем иной характер имеет движение частиц в жидкости или в твердом теле. Здесь у них вообще не бывает свободного пробега. В твердом теле атомы в основном совершают колебания около положений равновесия. А дальние прыжки происходят лишь изредка. При этом атом может либо «сесть» в междоузлие, потеснив соседние атомы (Рис. 1‑8а), либо, оторвавшись от своих соседей, прыгнуть на один из пустых узлов, которые всегда существуют в реальной решетке (Рис. 1‑8б). В обоих случаях достаточно буквально одного колебания на новом месте, чтобы забыть о направлении предыдущего прыжка. Это значит, что τ_с ~ 10^-13 с.

Рис. 1‑10

В жидкостях картина гораздо запутаннее. С одной стороны, взаимное расположение молекул сохраняет здесь заметную долю ближнего порядка. И это приводит к прыжкам того же типа, который характерен для твердого тела. С другой стороны, в жидкости возможны и небольшие перемещения, когда целая группа молекул подается разом в ту или другую сторону. Но, так или иначе, времена корреляции в этом случае тоже очень малы.

1.5.3.Комбинация , появившаяся в формуле , оказывается, определяет и величину коэффициента диффузии. Чтобы показать это, вычислим в картине случайных блужданий поток частиц, возникающий из-за неоднородности состава системы.

Пусть для простоты плотность числа частиц рассматриваемого сорта меняется только вдоль оси х. Будем следить за такой группой этих частиц, перемещения которых вдоль оси х за время t по абсолютной величине лежат вблизи значения ξ_i,. Если , то половина этих частиц в среднем сместится на расстояние ξ_i вправо, а половина — влево[7]. При этом сечение АА', перпендикулярное к оси х (Рис. 1‑9), пересекут, очевидно, те из них, которые находятся от него слева или справа на расстоянии, не превышающем величины ξ_i, и движутся в нужную сторону.

Эти области показаны на Рис. 1‑9 штриховкой. Их объем , где A — площадь сечения АА'. А число интересующих нас частиц в этих областях можно приближенно найти, умножив этот объем на плотность их числа, n_i, взятую в средних точках областей, 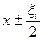. Здесь x — координата плоскости АА'.

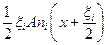Таким образом, за время t сечение АА' слева направо пересекут , а справа налево — частиц рассматриваемой группы. Это даст вклад в поток

.

А полный поток частиц рассматриваемого сорта через сечение АА' найдется суммированием этого выражения по всем возможным значениям абсолютной величины прыжка, ξ_i:

,

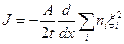мы внесли здесь ξ_i под знак производной, потому что это — заданное нами число. Оно не зависит от х.

При этом нужно, конечно, считать, что доля частиц, перемещающихся за время t на такие большие расстояния ξ_i, на которых заметно меняется плотность частиц, невелика. Иначе нельзя будет при всех ξ_i полагать 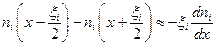. Это условие будет выполняться тем лучше, чем меньше τ_с (поскольку у нас ) и чем массивнее частицы. Либо, если этого нет, нужно уповать на малость градиентов.

Если п(х) — полная плотность числа частиц рассматриваемого сорта, то отношение п_i(х)/п(х) есть вероятность того, что частица, находящаяся вблизи плоскости АА' совершит за время t перемещение вдоль оси х величиной ξ_i. Поэтому

.

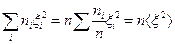Далее, если система изотропна, то средние квадраты перемещений по трем осям, 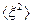, , 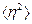, будут одинаковы: . Отсюда, воспользовавшись формулой , получаем для потока:

.

Это выражение имеет вид закона Фика с коэффициентом диффузии

.

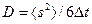Теперь формулу для среднего квадрата смещения частицы за время t можно записать в виде

.

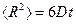Это соотношение было установлено Эйнштейном.

1.5.4.Формула для коэффициента диффузии, в принципе, годится для любых систем, твердых, жидких или газообразных. При ее выводе предполагалось лишь, что система изотропна. Однако ее универсальность в какой-то мере лишь кажущаяся, поскольку все различия между разными случаями запрятаны здесь в величине интервала Δt (который должен быть порядка или больше времени корреляции τ_c) и в среднем квадрате смещения частицы, , за это время. Этим величинам большей частью трудно придать точный количественный смысл, несмотря на их ясное физическое содержание. Но практически всегда для них можно получить полезные качественные оценки, как экспериментальные, так и теоретические.

При диффузии в газах легких частиц или частиц, чья масса сравнима с массой собственных молекул газа, интервал Δt проще всего выбрать порядка времени корреляции, которое, как мы говорили, примерно равно времени свободного пробега, τ.

Если же речь идет о диффузии небольшой примеси тяжелых (по сравнению с молекулами газа) частиц, то мы видели, что нужно выбирать , где τ — среднее время между двумя последовательными соударениями тяжелой частицы с легкими молекулами газа. 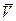Эти соударения мало меняют скорость тяжелой частицы, поэтому средний путь, проходимый ею за время τ_c, будет примерно в раз больше длины ее свободного пробега , где — средняя скорость тяжелой частицы. 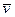Если учесть, что , где — средняя скорость молекул газа, то для коэффициента диффузии в этом случае легко получить простую оценку: .

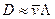Он определяется произведением скорости легких молекул на длинупробега тяжелых

При диффузии частиц в твердом теле время корреляции так мало, что для любого интервала можно считать 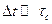. А заданной, скорее, является величина перемещения, имеющая порядок межатомных расстояний, d. Среднее время, за которое совершается такое перемещение, можно оценить из следующих соображений.

Чтобы оторваться от своих соседей и занять новое положение, атом должен случайно получить большую энергию активации, ε_a , порядка его энергии связи, ε_b,. Вероятность такого события в соответствии с каноническим распределением пропорциональна экспоненте 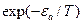. Поэтому частоту прыжков на соседние узлы можно оценить, умножив частоту попыток оторваться от своего окружения, ν, на 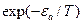. Но частота попыток оторваться есть просто частота колебаний атома: при каждом колебании он делает попытку уйти со своего места, но терпит неудачу и возвращается обратно. Поэтому среднее время, Δt, прыжка на расстояние d имеет порядок . Отсюда для коэффициента диффузии получаем оценку

.

В этой связи говорят, что диффузия в твердом теле является термически активированным процессом. При этом характерная величина энергии активации ε_a составляет 0,1—1 эВ. Качественно такая же температурная зависимость коэффициента диффузии наблюдается и в жидкостях. Только энергия активации здесь поменьше.