Экономическая постановка и общий вид математической модели задач нелинейного программирования.

В экономике и управлении имеется определенный ряд задач нелинейного характера, т.е. экономические показатели как-то нелинейного зависят от различных факторов.

f.e. зависит ….. стоимости от V продолжительности.

с/стоимость

V продолжительности

В этом классе задач выделяется 3 основных направления:

1) Дробно-линейное применение:

f.e. целевая функция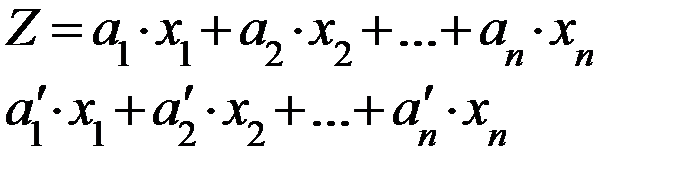

f.e. средняя стоимость V продолжительности, рентабельность ( )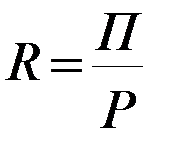

2) Квадратическое применение:целевая функция может содержать квадраты переменных и / или их произведения.

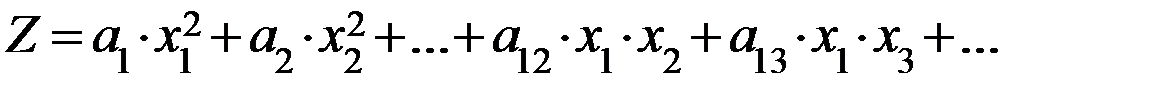
3) Выпуклое применение: класс считается наиболее простым, у которого целевая функция нелинейная, но выпуклая, а ограничения линейны или обратная задача (целевая функция линейна, а ограничения нелинейные).

Выпуклые функции - это функции, у которых отрезки, соединяющие 2 точки находятся в нутрии функции Ө

Линейное применение:

Ограничения: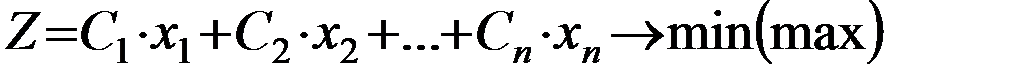

·

·

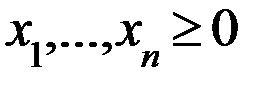
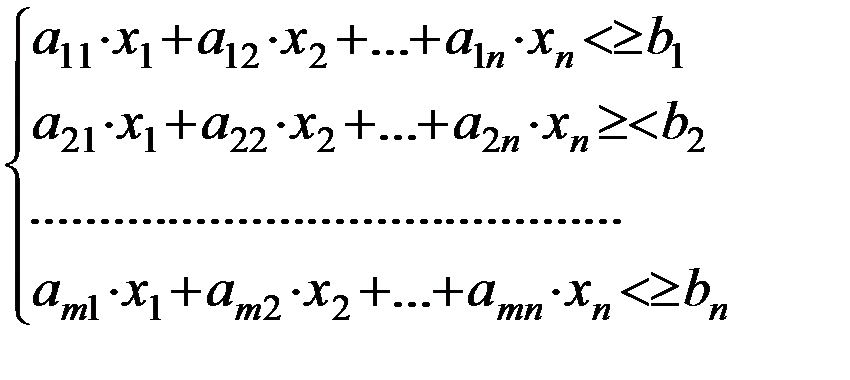
Задачи нелинейного применения:

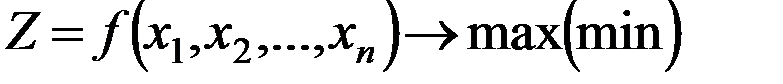
Ограничения:

·

·

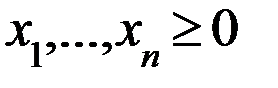
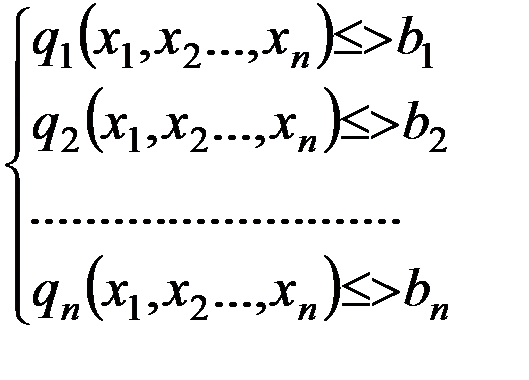
Геометрическая интерпретация задач линейного программирования.

Y нелинейная

X²+y²=1

1 оптимальное решение

ОДЗ

1 x

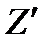
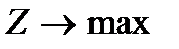
Z – прямая характеризующая целевую функцию f.e. линейная

y

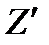
X

Z

ОДЗ- область допустимых значений

y

ОДЗ x

Z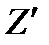

Если ОДЗ не линейна и не выпукла, то появляется понятие локального оптимума и глобального оптимума.

Глобальный оптимум – здесь достигается оптимальное значение целевой функции по сравнению с другой точкой допустимого пространства.

Локальный оптимум – значение целевой функции лучше, чем у соседних точек.

В линейном программировании базисное и оптимальное решение содержит столько переменных, сколько ограничений имеется в данной задаче. Для нелинейного программирования данная закономерность не соблюдается.