Формула Циалковского .

Формула (7) это приращение скорости , которое нужно сообщить КК , при переходе с одной круговой орбиты на другую . Возникает необходимость , при расчете о переходе КК с орбиты на орбиту , знать какое количество топлива необходимо для этого маневра .

Будем считать , что КК движется в воздушном пространстве и вне поля тяготения планеты (идеальный полет) .

Читаем , что сила тяги КК направлена по вектору скорости , т.е. движение можно рассматривать , как прямолинейное .

Запишем дифференциальные уравнения КК в проекции на вектор скорости .

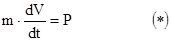
m – масса КК ;

V – скорость КК ;

P – тяга двигателей КК .

Так как движение КК происходит в безвоздушном пространстве , то можно записать :

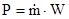
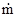- массовый секундный расход топлива ;

W – скорость истечения продуктов сгорания (ПС) на срезе сопла .

Подставим (**) в (*)

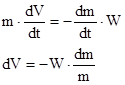
Проинтегрируем это выражение (W=const)

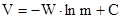
Для определения С используем начальные условия полета :

При t=0 : m=m₀ ; V=V₀

При t : m=m(t) ; V=V(t)

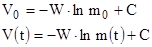
Рассмотрим приращение скорости за время t

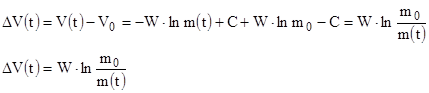
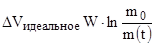- формула идеальной скорости (Циалковского) .

В реальных условиях величину импульса скорости ΔV необходимо увеличивать на некоторую величину ΔV_ПОТЕРЬ , которая возникает из-за наличия сил тяжести , действующих на КК , а также некомпланарности вектора тяги и вектора скорости , Таким образом :

ΔU+ΔV_ПОТЕРЬ=ΔV_{ХАРАКТЕРИСТИЧЕСКОЕ}

ΔV_ХАР – это реальная скорость , которая должна быть сообщена КК , для выполнения двух импульсного перелета .

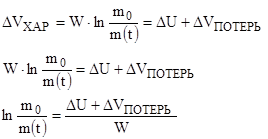
Рассмотрим случай :

m_o – стартовая масса ракеты ;

w_т – масса топлива ;

m_к – масса конструкции КК (сухой вес) .

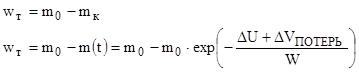
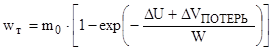
Формула показывающая , сколько нужно израсходовать топлива , чтобы сообщить КК дополнительную скорость (ΔU+ΔV_ПОТЕРЬ) .

В первом приближении ,когда нам неизвестны особенности КК , параметры орбиты и т.д. можно принять , что ΔV_ПОТЕРЬ≈0 и тогда

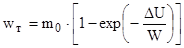
Полученная зависимость между величиной импульса (ΔU) необходимого для маневра и запаса топлива (w_т) позволяет нам ограничиться анализом потребного импульса скорости и не рассматривать характеристики самого КК , при решении многих задач механики космического полета .