Обратная фильтрация (деконволюция)

Сейсмическую трассу y(t) можно представить сверткой начального импульса s₀(t) и импульсной реакцией или оператором фильтра h(t), который характеризует воздействие среды на начальный импульс 8.1. или в спектральной области 8.2. Где Y(f) – амплитудо-частотная характеристика сигнала, S(f) – спектр начального сигнала, H(f) –АЧХ среды.

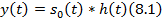
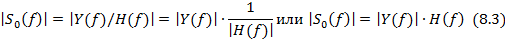
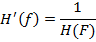
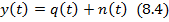
Где y(t) – трасса, q(t) – отраженная волна, n(t) – помехи.

Чтобы найти спектр начального сигнала нужно 8.3. Отсюда следует, что если к спектру сейсмической трассы применить фильтр H’(f), обратный характеристике среды, то мы получим спектр начального сигнала. С другой стороны если взять формулу 8.1. то, чтобы найти s­₀(t) нам нужно сделать процедуру обратную свёртке, т.е. деконволюцию.

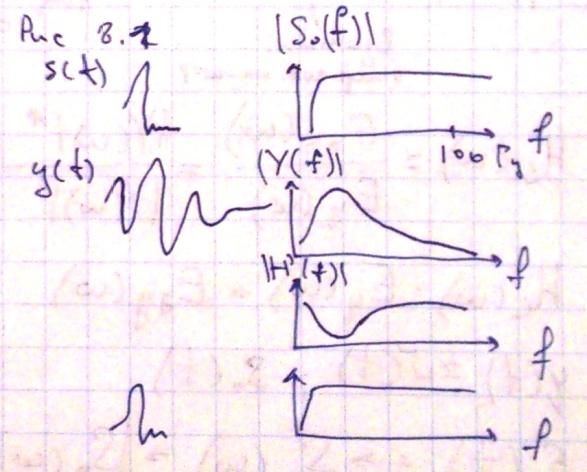При возбуждении колебаний у нас возникает сигнал, который считается коротким во времени, но этот сигнал обладает достаточно широким спектром. При распространении импульса в среде он меняется, рис 8.1. При этом с увеличением длительности сигнала, временная разрешающая способность записи уменьшается. Чтобы восстановить форму начального сигнала, нам нужно применить фильтр, частотная характеристика которого является обратной характеристике воздействия среды. Если перемножить эти частотные характеристики, то мы снова получим примерно начальный спектр начального сигнала и соответственно сигнал станет более коротким.

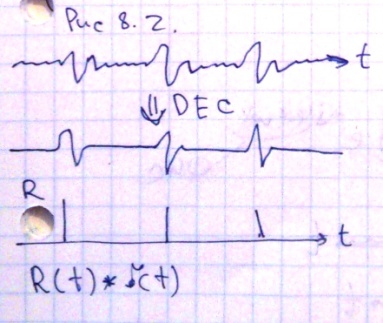Рис 8.2. в идеальном случае мы преобразуем наш начальный сигнал в единичный импульс, или импульс соответствующий коэффициентам отражения. В силу наличия различных помех, такой результат мы получить не можем, но тем не менее мы можем в той или иной степени (в зависимости от соотношения сигнал/помеха) сделать сигнал более коротким или решить ряд других задач.