Задачи на построение.
Задача.Даны a∩b=S, причем точка S расположена за пределами чертежа, и точка С 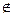 a, C
a, C 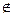 b. Построить прямую (CS).
b. Построить прямую (CS).
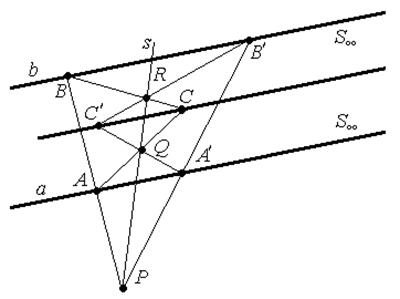
Решение. Задачу можно решить, применяя теорему Дезарга.
(недоступная точка чертежа отделена волнистой чертой).
Построение:
1. 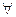 А, А′
А, А′ 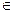 а и
а и 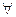 В, В′
В, В′ 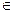 b.
b.
2. (АВ)∩(А′В′)= Р. Проведем 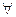 прямую через точку Р - s.
прямую через точку Р - s.
3. (АС)∩ s = Q и (ВС)∩ s= R.
4. (А′Q)∩(В′R)=С′, (СС′) - искомая прямая.
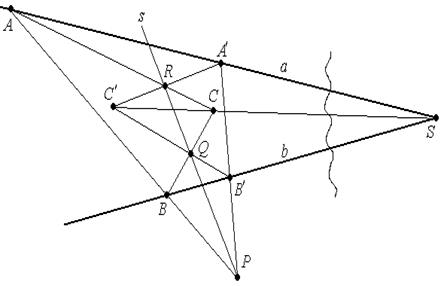
Замечание:Прямые а и b могут быть параллельными, задача решается аналогично. (Обоснуйте)
Опишите построение самостоятельно:
Простое отношение
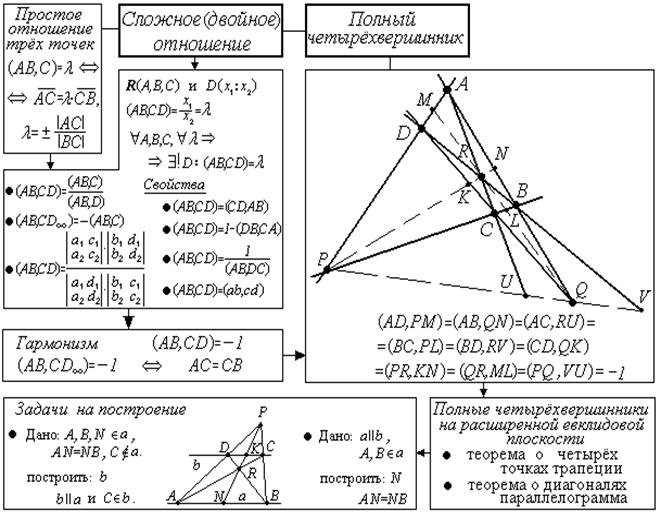
Среди любых трех точек лежащих на одной прямой (евклидовой), одна всегда лежит между двумя другими.
Определение: Простым отношением трех различных точек А, В, С 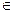 l называется число λ такое, что
l называется число λ такое, что 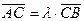 .
.
Тогда λ=± 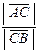 .
.
Обозначение: λ=(АВ,С)
Если С 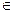 (АВ), тогда
(АВ), тогда 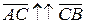 , а значит λ > 0.
, а значит λ > 0.
Если С 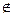 (АВ), тогда
(АВ), тогда 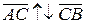 , а значит λ < 0.
, а значит λ < 0.
При λ = 0 получим 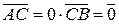
 А=С, при λ = - 1 получим
А=С, при λ = - 1 получим 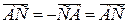
 А=В. Но точки А, В, С различны, значит λ ≠ 0 и λ ≠ - 1.
А=В. Но точки А, В, С различны, значит λ ≠ 0 и λ ≠ - 1.
На расширенной евклидовой плоскости 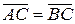 возможно в случае, когда С∞.
возможно в случае, когда С∞.
Будем считать на расширенной евклидовой прямой, что (АВ,С∞) = -1.
Пусть точки имеют аффинные координаты А(α), В(β), С(γ). Тогда вектор 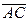 = ( γ - α ), а вектор
= ( γ - α ), а вектор 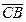 = ( β – γ ).
= ( β – γ ).
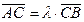
 ( γ - α ) = λ∙( β – γ )
( γ - α ) = λ∙( β – γ )  λ =
λ = 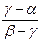 - здесь уже учтен знак простого отношения.
- здесь уже учтен знак простого отношения.
Схема для запоминания формула для вычисления

Задача. Даны аффинные координаты точек А(3), В(-2), С(2), М(3,5). Найти простые отношения (АВ,С), (ВС,А), (ВС,М), (СМ,А).
Решение.
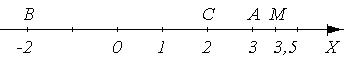
(АВ,С) = 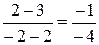 = 0,25, (
= 0,25, ( 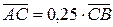 ).
).
(ВС,А) = 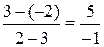 = -5, (
= -5, ( 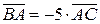 ).
).
(ВС,М) = 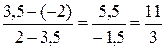 , (
, ( 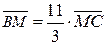 )
)
(СМ,А) = 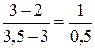 = 2, (
= 2, ( 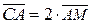 ).
).
Сложное отношение
На проективной прямой одна из трёх точек всегда лежит между двумя другими.

Нет смысла говорить о простом отношении трех точек. Необходима дополнительная точка.
Рассмотрим A, B, C, D, причем А, В, С – различны и D ≠ А.
Из первых трёх точек можно составить репер - R(А,В,С) и пусть точка D 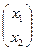 в этом репере.
в этом репере.
Определение: Число λ = 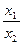 называется сложным (или двойным) отношением четырёх точек лежащих на одной прямой.
называется сложным (или двойным) отношением четырёх точек лежащих на одной прямой.
Обозначение: λ=(AB,CD).
Замечание: Так как D ≠ А 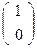 , значит х2 ≠ 0
, значит х2 ≠ 0  (AB,CD)=
(AB,CD)= 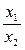 - всегда определено.
- всегда определено.
Теорема. Для 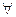 А, В, С - различных точек на проективной прямой и любого действительного числа λ существует единственная точка D на этой прямой такая, что (AB,CD) = λ.
А, В, С - различных точек на проективной прямой и любого действительного числа λ существует единственная точка D на этой прямой такая, что (AB,CD) = λ.
Доказательство. Так как А, В, С – различны, то они могут образовать репер R(А,В,С). Тогда в этом R(А,В,С) существует некоторая точка D с координатами 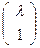 и по определению сложного отношения (AB,CD)=
и по определению сложного отношения (AB,CD)= 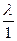 = λ (существование).
= λ (существование).
Докажем единственность от противного: Пусть существует еще одна точка D1 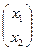 такая, что
такая, что
(AB,CD1)=λ= 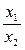
 х1=λ∙х2
х1=λ∙х2  D1
D1 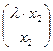 =
= 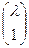 =D
=D  D1=D (единственность). □
D1=D (единственность). □
Вывод: По любым трем точкам и λ всегда можно найти четвертую.
Пусть А 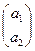 , В
, В 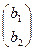 , С
, С 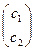 , D
, D 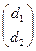 - различные точки.
- различные точки.
Возьмем первые три в качестве нового репера, если 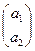 +
+ 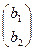 ≠
≠ 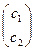 , то репер R′(А , В , С) не согласован. Согласуем репер:
, то репер R′(А , В , С) не согласован. Согласуем репер:
k1 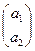 + k2
+ k2 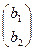 =
= 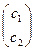
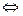
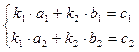
∆= 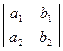 , ∆1=
, ∆1= 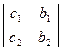 , ∆2=
, ∆2= 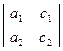
 k1 =
k1 = 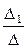 , k2 =
, k2 = 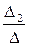 .
.
Тогда матрица преобразования координат - M= 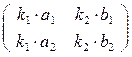 .
.
Обратная для неё- M-1 = 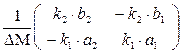 .
.
По формулам преобразования координат: μ DR′ = М-1 ∙ DR
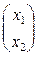 =
= 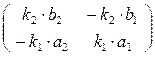 ∙
∙ 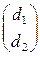 =
= 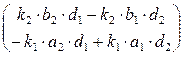
Множитель 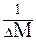 можно отбросить. (Почему?)
можно отбросить. (Почему?)
 (AB,CD) =.
(AB,CD) =. 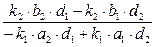 =
= 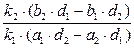 =
= 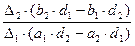
= 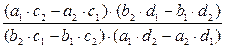
Эту формулу можно записать с помощь определителей (проверьте самостоятельно):
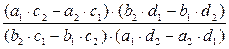 =
= 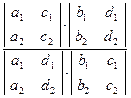
Схема для запоминания формула для вычисления
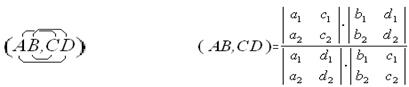
Свойства:
1. Сложное отношение не зависит от выбора репера.
Доказательство основано на формулах перехода к новому реперу
λ ХR =А∙XR′ и μ XR′ = А-1 ∙ ХR и свойствах определителя.
2. При перестановке пар сложное отношение не меняется: (AB,CD) =( CD, AB).
3. При перестановке точек в паре сложное отношение меняется на обратное:
(AB,CD)= 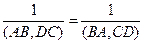 .
.
Доказательство свойств 1 - 3.Самостоятельно.
4. При перестановке крайних точек сложное отношение меняется на дополнительное к единице. При перестановке внутренних точек сложное отношение меняется на дополнительное к единице.
(AB,CD) = 1 - (DB,CA) или (AB,CD)= 1 - (AC,BD).
Доказательство. Рассмотрим репер из первых трёх точек А, В, С и пусть точка D 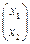 в этом репере,тогда(АВ,СD)=
в этом репере,тогда(АВ,СD)= 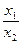 = λ .
= λ .
(DВ,СА)= 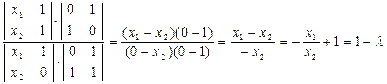
Докажите это свойство другим способом.
Из точек A, B, C, D можно составить 24 комбинации сложных отношений точек (4!) , некоторые из них будут совпадать. Например (AB,CD) =( CD, AB) = (DC,BA) = (BA,DC) (проверьте).
Таким образом, будет 6 различных сложных отношений (проверьте).
(AB,CD) = λ → 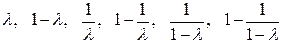 .
.
Определение: Если (AB,CD) > 0, то говорят, что пара AB не разделяет пару CD. Если (AB,CD) < 0, то говорят, что пара AB разделяет пару CD.
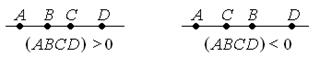
5. (AB,CD) = 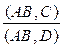 (поэтому сложное отношение называется двойным).
(поэтому сложное отношение называется двойным).
Доказательство. Рассмотрим однородную проективную систему координат. Пусть известны аффинные координаты точек А(α), В(β), С(γ), D (δ), тогда их проективные координаты будут
А 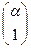 , В
, В 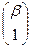 , С
, С 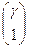 , D
, D 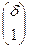 .
.
С одной стороны (AB,CD) = 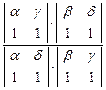 =
= 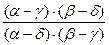 .
.
С другой стороны (AB,C) = 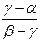 и (AB,D) =
и (AB,D) = 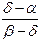

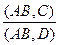 =
= 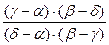 =
= 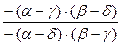 =
= 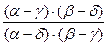 □
□
6. Если D∞ - несобственная точка, тогда (AB,CD∞) = - (AB,C).
Доказательство. Рассмотрим однородную проективную систему координат R(Е1∞, Е2, Е). Пусть известны аффинные координаты собственных точек А(α), В(β), С(γ), тогда их проективные координаты будут А 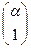 , В
, В 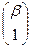 , С
, С 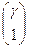 .
.
Так как точка D несобственная, то D=Е1∞,  D
D 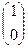 .
.
С одной стороны (AB,CD∞) = 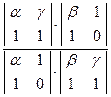 =
= 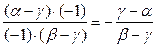 .
.
С другой стороны (AB,C) = 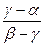 .
.
Попробуйте доказать это свойство другим способом. □
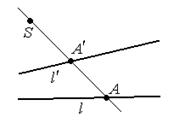 Определение: Центральной проекцией прямой ℓ на прямую ℓ' из точки S называется отображение, при котором каждой точке А прямой ℓ ставится в соответствие точка А'прямой ℓ'
Определение: Центральной проекцией прямой ℓ на прямую ℓ' из точки S называется отображение, при котором каждой точке А прямой ℓ ставится в соответствие точка А'прямой ℓ'
такая что А'= ℓ' ∩ (SА).
7. При центральном проектировании сложное отношение четырёх точек, лежащих на одной прямой не меняется. (AB,CD)=(A'B',C'D').
Доказательство. (AB,CD) =λ, доказать, что (A'B',C 'D') = λ.
 На прямой (SС) возьмем точку Е и рассмотрим репер
На прямой (SС) возьмем точку Е и рассмотрим репер
R( А, В, S, Е).
Тогда А 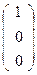 , В
, В 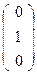 , S
, S 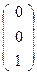 , Е
, Е 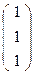 .
.
D 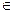 (АВ)
(АВ)  D
D 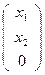 , С=Е30=
, С=Е30= 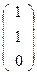 .
.
Тогда в согласованном репере R(А,В,С) - D 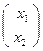
 (AB,CD)=
(AB,CD)= 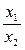 =λ (обоснуйте).
=λ (обоснуйте).
А' 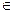 (АS)
(АS)  А'
А' 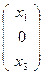 , сократим на х1 , получим
, сократим на х1 , получим 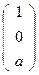 .
.
В' 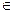 (ВS)
(ВS)  В'
В' 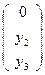 , сократим на у2 , получим
, сократим на у2 , получим 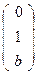 .
.
Рассмотрим репер R'(А',В',S,Е). Он не согласован т.к. 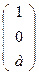 +
+ 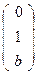 +
+ 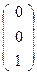 ≠
≠ 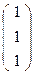 .
.
Решая систему 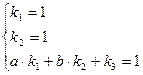 , получим k1 = 1, k2 = 1, k3 = - а – b.
, получим k1 = 1, k2 = 1, k3 = - а – b.
Тогда, М 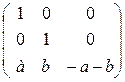 и М -1
и М -1 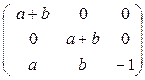
Пусть точка D в репере R' имеет координаты 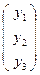 , тогда по формулам преобразования координат μ ХR′ =М-1 ∙ХR
, тогда по формулам преобразования координат μ ХR′ =М-1 ∙ХR
DR′ = 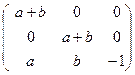 ·
· 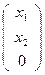 =
= 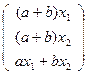

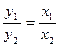 .
.
СR′ = 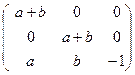 ·
· 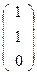 =
= 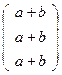 =
= 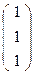 .
.
Так как точка D' является проекцией точки D из точки S (вершины нового репера) на координатную прямую (А'В'), то по теореме о проекциях D'R′= 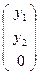 . Точка С' является проекцией точки С из точки S на (А'В'), то С'R′=
. Точка С' является проекцией точки С из точки S на (А'В'), то С'R′= 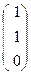 . Значит в репере из точек А', В', С' точка D'
. Значит в репере из точек А', В', С' точка D' 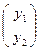 ,
,
тогда (A'B',C 'D')= 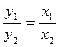 . □
. □
Замечание: Это свойство позволяет вычислять сложное отношение для точек, заданных своими координатами на проективной плоскости.
Задача. Найти сложное отношение точек A 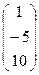 , B
, B 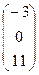 , C
, C 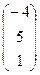 , D
, D 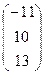 .
.
Решение. Проверим коллинеарность точек.
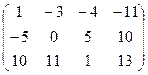 ~
~ 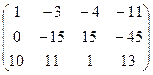 ~
~ 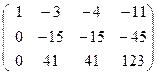 ~
~ 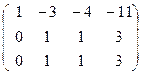 ~
~ 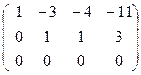
 rang = 2
rang = 2  точки коллинеарны.
точки коллинеарны.
(Какими ещё способами можно проверить коллинеарность точек?)
Спроектируем точки из какой-либо вершины репера на какую-либо координатную прямую. Например, из Е3 на (Е1Е2), получим точки
A3 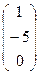 ,B3
,B3 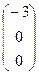 ,C3
,C3 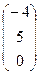 ,D3
,D3 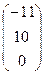 .
.
В репере R( Е1, Е2, Е30) эти точки будут иметь координаты A3 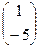 ,B3
,B3 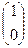 ,C3
,C3 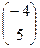 ,D3
,D3 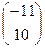 .
.
По свойству (7) получим
 (AB,CD) = (A3B3 ,C3D3) =
(AB,CD) = (A3B3 ,C3D3) = 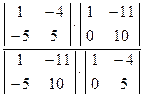 =3.
=3.
Замечание: Проверка коллинеарности точек на плоскости обязательна!
Замечание: Это свойство позволяет вводить понятие сложного отношения четырёх прямых пучка. Проводя любую прямую, не принадлежащую пучку, мы будем получать четвёрки точек с одинаковым сложным отношением.
Определение: Сложным отношением 4 прямых пучка будем называть число (ab,cd) = (AB,CD).
Задача. Найти сложное отношение прямых а: х1 – 3х2 + 5х3 =0, b: 4х1 + 3х2 - х3 =0,
c: 2х1 – х2 + 3х3 =0, d: 3х1 – 4х2 + 8х3 =0.
Решение.
Первый способ: Проверим принадлежность прямых одному пучку.
Найдем точку пересечения прямых а и b:
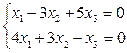 →
→ 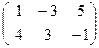 →
→ 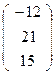 или
или  - М.
- М.
Проверим, принадлежит ли точка М прямым с и d:
для прямой с: 2∙(-4) – 7 + 3∙5= 0, для прямой d: 3∙(-4) - 4∙7 + 8∙5 = 0.
 прямые принадлежат одному пучку. (Какими ещё способами можно проверить принадлежность прямых одному пучку?)
прямые принадлежат одному пучку. (Какими ещё способами можно проверить принадлежность прямых одному пучку?)
Выберем любую прямую не проходящую через точку М, например прямую (Е2Е3), её уравнение х1 = 0. Найдем точки пересечения данных прямых с прямой (Е2Е3):
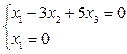 →
→ 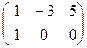 →
→ 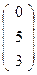 - точка А,
- точка А,
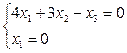 →
→ 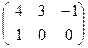 →
→ 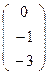 или
или 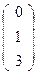 - В,
- В,
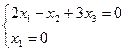 →
→ 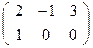 →
→ 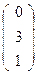 - точка С,
- точка С,
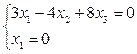 →
→ 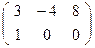 →
→ 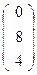 или
или 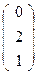 - D.
- D.
Точки лежат на прямой (Е2Е3), найдем их сложное отношение:
(AB,CD) = 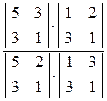 =
= 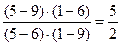 = 2,5
= 2,5  (ab,cd)=2,5.
(ab,cd)=2,5.
Второй способ. Применим принцип двойственности:
а: х1–3х2+5х3=0, → A 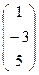 , b: 4х1+3х2-х3=0, → B
, b: 4х1+3х2-х3=0, → B 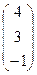 ,
,
c: 2х1–х2+3х3=0, → C  , d: 3х1–4х2+8х3=0, → D
, d: 3х1–4х2+8х3=0, → D 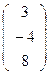 .
.
Принадлежность прямых одному пучку  коллинеарности точек.
коллинеарности точек.
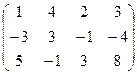 ~
~ 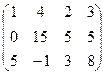 ~
~ 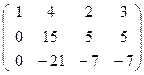 ~
~ 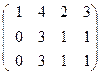
 rang = 2
rang = 2  точки коллинеарны.
точки коллинеарны.
Спроектируем точки из какой-либо вершины репера на какую-либо координатную прямую. Например из Е2 на (Е1Е3 ), получим точки A2 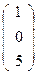 , B2
, B2  , C2
, C2 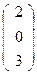 , D2
, D2 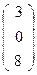 .
.
В репере R( Е1, Е3, Е20) эти точки будут иметь координаты A2 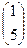 , B2
, B2 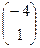 , C2
, C2 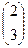 , D2
, D2 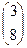 .
.
По свойству (7) получим (AB,CD) = (A2B2 ,C2D2)= 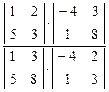 =2,5.
=2,5.
Рассмотрим частные случаи сложного отношения.
Пусть репер R( А, В, С).
1. В=D  D
D 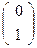
 (AB,CD) =
(AB,CD) = 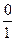 = 0.
= 0.
2. С=D  D
D 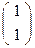
 (AB,CD) =
(AB,CD) =  = 1.
= 1.
3. А=D  D
D 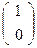
 (AB,CD) =
(AB,CD) = 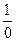 - не существует.
- не существует.
Вывод: Точка D может совпадать с любой точкой кроме точки А.
Гармонизм
Определение: Если (AB,CD) = - 1, то четверка точек A,B,C,D называется гармонической.
Рассмотрим гармоническую четверку точек (AB,CD) = -1.
По свойству (2)  (CD, AB) = (AB,CD) = -1.
(CD, AB) = (AB,CD) = -1.
По свойству (3)  (AB,DC) =
(AB,DC) = 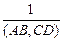 = -1.
= -1.
Вывод: При перестановке пар и/или точек в паре гармонизм не нарушается.
Теорема. Четвёрка точек A, B,C, D∞ - гармоническая тогда и только тогда, когдаточка C - середина AB . (третья точка – середина отрезка из первых двух).
Доказательство. C – середина AB  (AB,C) = 1.
(AB,C) = 1.
 По свойству (6)
По свойству (6)  (AB,CD∞) = - (AB,C) = - 1 - гармоническая четвёрка. В обратную сторону докажите самостоятельно □
(AB,CD∞) = - (AB,C) = - 1 - гармоническая четвёрка. В обратную сторону докажите самостоятельно □
Построение гармонических четвёрок.
Задача 1. В пучке П(S) даны три прямые а, b, с. Построить прямую d такую, что (аb, сd) = -1.
Решение. Сложное отношение прямых пучка определяется сложным отношением точек пересечения этих прямых с какой-либо прямой не инцидентной пучку. Мы должны подобрать прямую таким образом, чтобы точки пересечения давали некоторый отрезок вместе с его серединой, тогда по теореме четвёртая гармоническая точка будет несобственной точкой. А значит, четвёртая гармоническая прямая в пучке будет параллельна подобранной прямой.
 Построение:
Построение:
1. На третьей прямой с выбираем 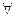 М.
М.
2. Через неё проводим прямые параллельные а и b. (АМ)|| b и (ВМ)|| а
3. А=(АМ)∩а и В=(ВМ)∩b.
4. С=(АВ) ∩ с.
5. Четырехугольник АSВМ – параллелограмм, по свойству параллелограмма точка пересечения диагоналей является серединой диагонали. Т.е. С середина АВ. По теореме
четвертая гармоническая точка будет
несобственной, т.е. D∞ .
6. Искомая прямая - d=(SD∞).
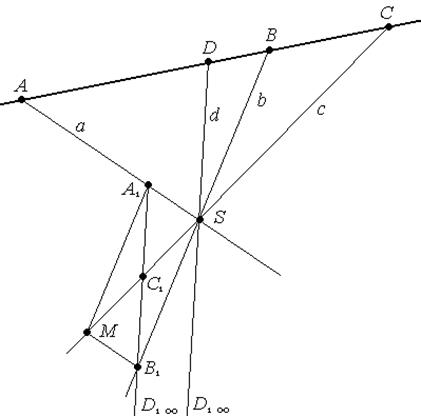
Задача 2. В на прямой даны три точки A, B, C. Построить точку D такую, что (AB,CD) = -1.
Решение. Будем использовать предыдущую задачу Возьмем  S'
S'  (АВ).
(АВ).
Обозначим а=(АS'), b=(ВS), с=(СS'). Далее решение задачи 1.
Опишите последовательность построения самостоятельно.
Дата добавления: 2022-02-05; просмотров: 705;











