Преобразование координат
Рассмотрим проективную прямую Р1 и два репера
R(Е1 ,Е2 ,Е) и R′(Е′1 ,Е′2 , Е′). Пусть известны координаты точек второго репера в первом репере:
Е′1 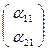 , Е′2
, Е′2 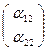 , Е′
, Е′ 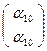 , т.е. ē′1 = α11 ē1+ α21 ē2, ē′2 = α12 ē1 + α22 ē2 , ē′ = α10 ē1 + α20 ē2 .
, т.е. ē′1 = α11 ē1+ α21 ē2, ē′2 = α12 ē1 + α22 ē2 , ē′ = α10 ē1 + α20 ē2 .
В общем случае репер R′(Е′1 ,Е′2 ,Е′) может оказаться не согласованным (ē′1+ ē′2 ≠ ē′). Согласуем точки второго репера, т.е. найдем такие числа k1 и k2 , что ē′ = k1ē′1 + k2ē′2 , для этого необходимо решить систему: 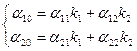 .
.
Пусть матрица системы А 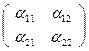 ,тогда ∆А≠0 (почему?).
,тогда ∆А≠0 (почему?).
Система имеет единственное решение (k1 , k2) и тогда будем считать координатами точек Е′1 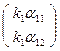 и Е′2
и Е′2 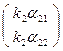 , репер в этом случае будет согласованным.
, репер в этом случае будет согласованным.
Замечание: В дальнейшем будем считать, что второй репер – согласован (если нет, то мы знаем, как его согласовать).
Пусть точка Х 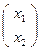 в репере R и та же точка в репере R′ имеет координаты
в репере R и та же точка в репере R′ имеет координаты 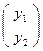 .
.
Тогда вектор 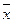 , порождающий эту точку может выражаться через вектора первого и второго базисов:
, порождающий эту точку может выражаться через вектора первого и второго базисов: 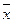 = х1 ∙ē1 + х2 ∙ē2 или
= х1 ∙ē1 + х2 ∙ē2 или 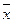 = у1∙ē′1 + у2∙ē′2
= у1∙ē′1 + у2∙ē′2

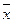 = у1∙ē′1 + у2∙ē′2 = у1∙(α11∙ē1 + α21∙ē2)+ у2∙(α1∙ē1 + α22∙ē2) = =(у1∙α11+ у2∙α12)∙ē1+ (у1∙α21+ у2∙α22)∙ē2 = х1∙ē1+ х2∙ē2
= у1∙ē′1 + у2∙ē′2 = у1∙(α11∙ē1 + α21∙ē2)+ у2∙(α1∙ē1 + α22∙ē2) = =(у1∙α11+ у2∙α12)∙ē1+ (у1∙α21+ у2∙α22)∙ē2 = х1∙ē1+ х2∙ē2  х1 = у1∙α11 + у2∙α12 и х2 = у1∙α21 + у2∙α22 ,
х1 = у1∙α11 + у2∙α12 и х2 = у1∙α21 + у2∙α22 ,
или 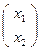 =
= 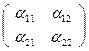 ∙
∙ 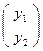 , в матричной записи: ХR =A∙XR′ ,
, в матричной записи: ХR =A∙XR′ ,
где ХR - столбец координат точки Х в первом (старом) репере,
а XR′ - столбец координат той же самой точки Х во втором (новом) репере.
Матрица А 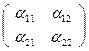 будет матрицей перехода от старого репера к новому реперу.
будет матрицей перехода от старого репера к новому реперу.
Замечание: Матрица Аявляется невырожденной. (Почему?).
Вывод: Зная матрицу перехода и координаты точки в новом репере можно находить координаты точки в старом репере:
ХR =A∙XR′ │∙А-1 слева
А-1 ∙ ХR =А-1∙A∙XR′ = XR′  XR′ = А-1 ∙ ХR .
XR′ = А-1 ∙ ХR .
Вывод:Формулы преобразования координат точек при переходе к другому реперу имеют вид:
λ ХR =A∙XR′ и μ XR′ = А-1 ∙ХR .
Аналогичные рассуждения можно применить для Р2,
Пусть Е'1 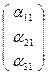 , Е'2
, Е'2 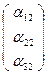 , Е'3
, Е'3 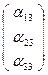 , Е'
, Е' 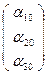 .
.
Для согласования второго репера будем находить k1 , k2 , k3 .
Получим матрицу третьего порядка А.
Формулы преобразования координат точек будут такими же:
λ ХR =A∙XR′ и μXR′ = А-1∙ХR .
Рассмотрим прямую и∙Х=0.
Пусть её координаты в старом репере - иR и в новом - uR′ .
Уравнение прямой в старом репере иR ∙ХR=0, в новом иR′ ∙ХR′=0.
Подставим формулы преобразования координат, получим 0= иR∙ХR = иR∙A∙XR′ = иR′ ∙ХR′ ,
где иR∙A=иR′ или λ иR′= иR∙A, тогда μ иR = иR′ ∙A-1 .
Вывод: Формулы преобразования координат точек и прямых на проективной плоскости имеют вид:
Для точек λ ХR =A∙XR′ и μ XR′ = A -1 ∙ХR .
Для прямых λ иR′= иR ∙A и μ иR = иR′ ∙A -1.
Замечание:Обратите внимание на умножение матриц: для точек матрица перехода умножается слева, а для прямых справа.
Задача. Даны два репера R(Е1 , Е2 , Е3 , Е) и R′(Е′1 , Е′2 , Е′3 , Е′). Известны координаты точек второго репера в первом:
Е′1 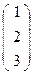 , Е′2
, Е′2  , Е′3
, Е′3 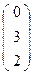 , Е′
, Е′ 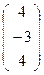 .
.
Найти формулы преобразования координат при переходе от одного репера к другому. Найти координаты точки М во втором репере если известны её координаты в первом МR 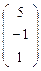 . Найти координаты точки К в первом репере если известны её координаты во втором КR ′
. Найти координаты точки К в первом репере если известны её координаты во втором КR ′ 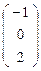 .
.
Найти уравнение прямой а :5 х1 - 2 х2+3 х3 = 0 в новом репере.
Решение. Проверим, согласованы ли точки второго репера:
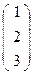 +
+  +
+ 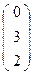 =
= 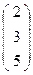 ≠
≠  - второй репер не согласован.
- второй репер не согласован.
Согласуем его, для этого решим систему 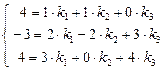 ,
,
её решением будет: k1 = 2, k2 = 2, k3= -1,
тогда матрица перехода будет A 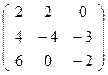 ,
,
обратной является A-1= 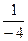
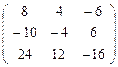 =
= 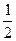
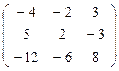 .
.
Так как координаты определяются с точностью до пропорциональности коэффициент 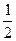 можно отбросить.
можно отбросить.
Формулы преобразования координат примут вид:
λХR= 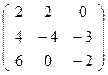 ∙XR′ и μXR′ =
∙XR′ и μXR′ = 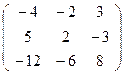 ∙ХR .
∙ХR .
μМR′ = A -1 ∙МR = 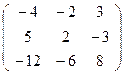 ∙
∙ 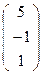 =
= 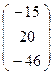 .
.
λКR=A ∙КR′ = 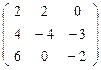 ∙
∙ 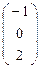 =
= 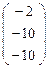 , с учетом пропорциональности координаты точки К в старом репере будут
, с учетом пропорциональности координаты точки К в старом репере будут 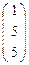 .
.
λ аR′= аR∙A= 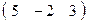 ∙
∙ 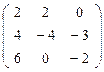 =
= 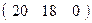 , с учетом пропорциональности координаты прямой будут
, с учетом пропорциональности координаты прямой будут 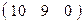
 аR′ : 10 х′1 + 9 х′2 = 0
аR′ : 10 х′1 + 9 х′2 = 0
Дата добавления: 2022-02-05; просмотров: 636;











