Принцип двойственности
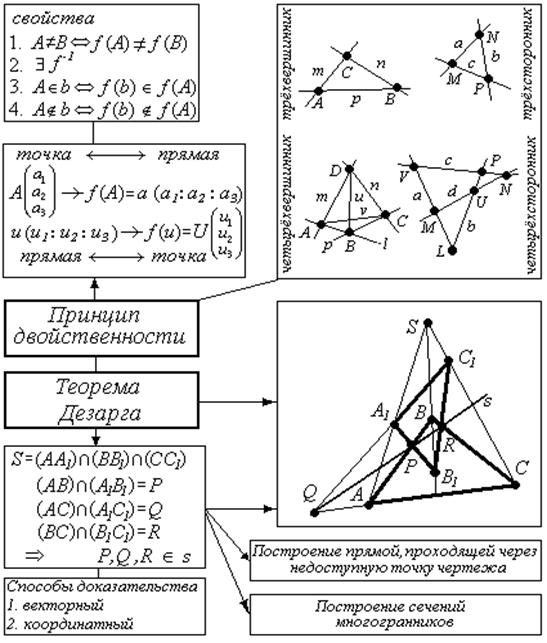
Пусть на P2 фиксирован репер R(Е1 , Е2 , Е3 , Е), пусть даны какие-либо точка А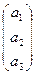 
и прямая и (и1 : и2 : и3).
Рассмотрим отображение f : P2 → P2 такое, что точке в соответствие ставится прямая с такими же координатами, а прямой – точка:
А 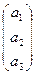→ f (А)=а ( а1 : а2 : а3) и и( и1 : и2 : и3) → f (и) = 
.
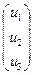Определение: Такое отображение называется корреляция.
Свойства:
1. А≠В 
f (А) ≠ f (В)
2. 
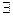f -1.
Теорема. Корреляция сохраняет отношение принадлежности.
Доказательство. Докажем, что А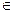 
и f (и) 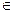f (А).
Пусть А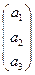 
и прямая и ( и1 : и2 : и3), т.е. и1 х1 + и2 х2 + и3 х3 = 0.
Если А 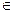и и1 а1 + и2 а2 + и3 а3 = 0.
f (А)=а ( а1 : а2 : а3), значит а1 х1 + а2 х2 + а3 х3 = 0.
f (и) = U 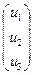и f (и) 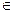f (А) а1 и1 + а2 и2 + а3 и3 = 0.
Очевидно, что эти условия одинаковы. □
Замечание: Таких отображений может быть много, они зависят от репера.
Замечание: В дальнейшем вместо термина «принадлежность» будем применять термин «инцидентность».
Примеры: «точка принадлежит прямой» ↔ «точка инцидентна прямой», или «прямая проходит через точку» ↔ «прямая инцидентна точке», или «две прямые пересекаются в одной точке» ↔ «две прямые инцидентны одной точке»
Вывод: Точки и прямые ведут себя одинаково.
Таким образом, можем сформулировать следующий принцип.
Малый принцип двойственности: Пусть верно некоторое предложение, касающееся точек и прямых и отношения инцидентности на проективной плоскости Р2 , тогда будет верным предложение в котором слово «точка» заменено на слово «прямая», слово «прямая» заменено на слово «точка», отношение инцидентности не меняется.
Это принцип справедлив в силу свойств заданного выше отображения и теоремы. Вспомним свойства проективного пространства.
· Через две точки проходит одна прямая - Двум точкам инцидентна одна прямая.
· Две прямые пересекаются в одной точке - Двум прямым инцидентна одна точка.
Такие предложения называются двойственными.
Двойственными могут быть фигуры на проективной плоскости.
Определение: Фигура, состоящая из трёх различных точек, не лежащих на одной прямой и трёх прямых, проходящих через эти точки, называется трёхвершинником. Точки называются вершинами, а прямые сторонами.
Замечание: На расширенной евклидовой плоскости трёхвершинник может иметь несобственные точки. (Сколько?).
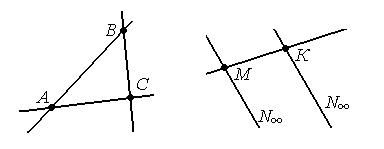
Обозначение: ∆АВС или ∆МКN∞ .
Двойственной фигурой будет фигура, состоящая из трёх различных прямых не инцидентных одной точке и трёх точек не лежащих на одной прямой. Такую фигуру можно назвать трёхсторонником, но она состоит из тех же элементов что и трёхвершинник. Поэтому трёхвершинник считается фигурой, двойственной самой себе и термин «трехсторонник» обычно не применяют.
Определение: Фигура, состоящая из четырёх различных точек, среди которых никакие три не лежат на одной прямой и шести прямых, проходящих через эти точки, называется четырёхвершинником.
Замечание: На расширенной евклидовой плоскости четырёхвершинник может иметь несобственные точки. (Сколько?).
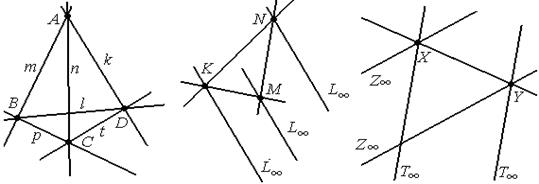
Обозначение: АВСD, или МКNL∞ , или ХYZ∞T∞ .
Рассмотрим четырёхвершинник АВСD. Точки А, В, С, D – вершины, прямые (АВ), (АС), (АD), (ВС), (ВD), (СD) - стороны.
Определение: Стороны, не имеющие общих вершин, называются противоположными: (АВ) и (СD), (АС) и (ВD), (АD) и (ВС) – пары противоположных сторон.
Определение:Точки пересечения противоположных сторон называются диагональными точками
Определение:Трёхвершинник, составленный из диагональных точек называется диагональным трёхвершинником, а его стороны называются диагоналями.
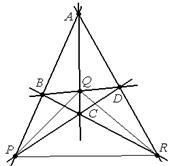
Например, четырёхвершинник АВСD
(АВ)∩(СD)=Р,
(АС)∩(ВD)=Q,
(АD)∩(ВС)=R,
∆PQR - диагональный трёхвершинник, а прямые (PQ), (PR), (QR) – диагонали.
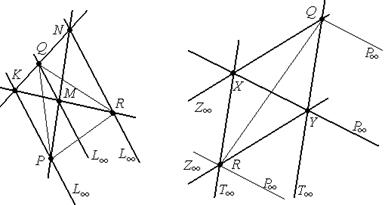
Четырехвершинники МКNL∞ и ХYZ∞T∞ :
Двойственной фигурой будет фигура, состоящая из четырёх различных прямых среди которых никакие три не инцидентны одному пучку и шести точек пересечения этих прямых. Такую фигуру называют четырёхсторонником.
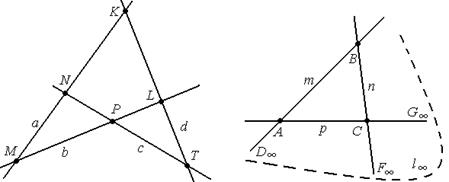
Обозначение: abcd или mnpl∞
Теорема Дезарга
Теорема. Пусть даны два ∆АВС и ∆А′В′С′ между вершинами, которых установлено соответствие (А↔А′, В↔В′, С↔С′).
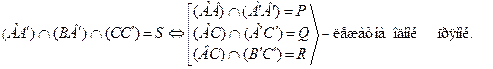
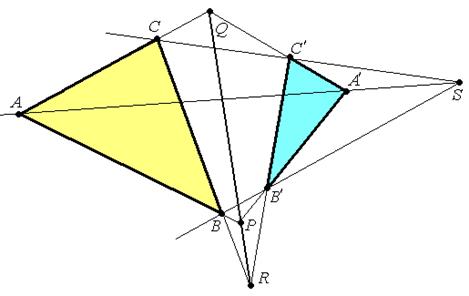
Доказательство. Нам даны два трехвершинника ∆АВС и ∆А′В′С′, причем (АА′)∩(ВВ′)∩(СС′) = S .
Пусть (АВ)∩(А′В′)=Р, (АС)∩(А′С′)=Q, (ВС)∩(В′С′)=R.
Докажем, что точки Р, Q, R - принадлежат одной прямой. Обозначим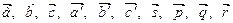 
- векторы, порождающие соответствующие точки.
Точка S 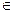(АА′) 
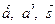- линейно зависимы 
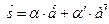(1)
Точка S 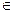(ВВ′) 
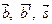- линейно зависимы 
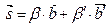(2)
Точка S 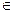(СС′) 
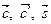- линейно зависимы 
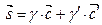(3)
Рассмотрим разности этих равенств:
(2) - (1):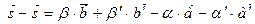 
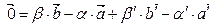
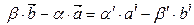- вектор который зависит от 
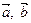, а значит точка порождаемая этим вектором лежит на прямой (АВ), в то же время этот вектор зависит от 
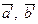, а значит точка лежит на прямой (А′В′). Т.е. эта точка является пересечением прямых (АВ) и (А′В′) 
это точка Р 
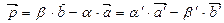
(3) - (1):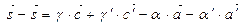 
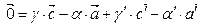
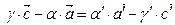- вектор который зависит от 
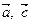, а значит точка порождаемая этим вектором лежит на прямой (АС), в то же время этот вектор зависит от 
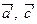, а значит точка лежит на прямой (А′С′). Т.е. эта точка является пересечением прямых (АС) и (А′С′)
это точка Q 
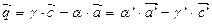
(3) - (2):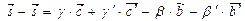 
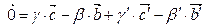
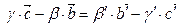- вектор который зависит от 
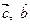, а значит точка порождаемая этим вектором лежит на прямой (BС), в то же время этот вектор зависит от 
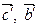, а значит точка лежит на прямой (B′С′). Т.е. эта точка является пересечением прямых (BС) и (B′С′)
это точка R 
.
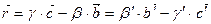Итак: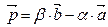 
, 
, 
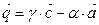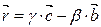
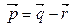
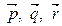- линейно зависимы точки Р, Q, R - принадлежат одной прямой. □
Замечание: Теорема, двойственная теореме Дезарга, тоже будет верна в силу принципа двойственности. (Самостоятельно).
Замечание: Теорема Дезарга справедлива и в случае, если трёхвершинники лежат в разных плоскостях.
Конфигурация Дезарга состоит из 10 точек и 10 прямых. На каждой прямой 3 точки через каждую точку проходит 3 прямые. Конфигурация Дезарга двойственна сама себе.
Определение: Точка S - называется центром конфигурации, дезарговой точкой или дезарговым центром.
Определение: Прямая, содержащая точки P, Q, R - называется осью конфигурации, дезарговой осью или дезарговой прямой.
Замечание:Любая точка в конфигурации может быть дезарговой точкой. Любая прямая может быть дезарговой прямой.
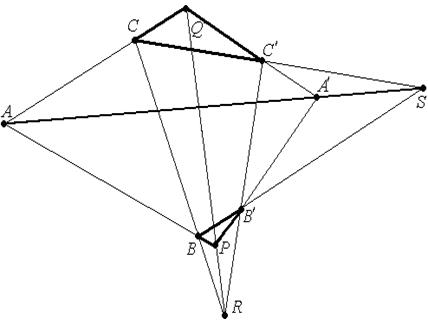
Задача. Найти трехвершинники в конфигурации Дезарга, если дезаргов центр - точка А.
Решение. А=(СQ)∩(SА′)∩(ВР), остались точки С′, В′, R – они образуют дезаргову ось:
С′=(А′Q)∩(СS), В′=(А′Р)∩(ВS), R=(QР)∩(СВ).
Теперь можно увидеть из каких точек состоят трёхвершинники, это тройки точек А′, Q, Р и В, С, S.
Осталось установить соответствие: А′↔S, Q↔С, Р↔В, ∆А′QР и ∆SСВ.
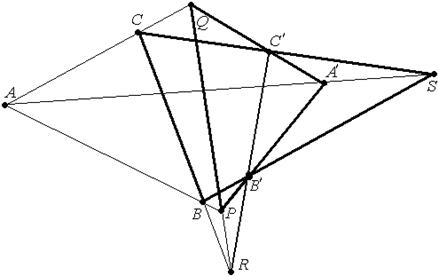
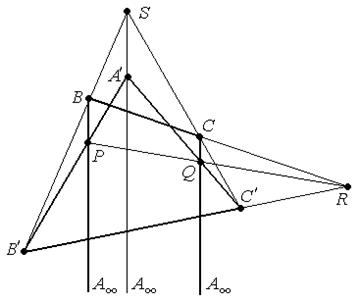
Задача. Найти трехвершинники в конфигурации Дезарга, если дезаргова ось – (АА′).
Решение. На прямой (АА′) лежит ещё одна точка - S. А=(СQ)∩(ВР),
А′=(С′Q)∩(В′Р),
S=(С′С)∩(В′В).
Теперь можно увидеть из каких точек состоят трёхвершинники, это тройки точек С, С′, Q и В, В′, Р.
Осталась точка R - она является дезарговым центром - R=(ВС)∩(В′С′)∩(QР)
В′↔С′, В↔С, Q↔Р, ∆В′ВР и ∆С′СQ.
Замечание: На расширенной плоскости конфигурация Дезарга может содержать несобственные элементы. (Сколько и какие?)
Дата добавления: 2022-02-05; просмотров: 252;
Поиск по сайту
Узнать еще
- I. Понятие о принципах обучения, их взаимосвязь.
- III. Общий принцип сочетания методов в процессе обучения.
- III. Части речи и принципы их классификации
- IV. Критерии и принципы обеспечения безопасности
- IV. Основные принципы этикета государственного служащего
- VIII. Принципы развивающего обучения.
- А.7 Устройство и принципы действия адсорбционных аппаратов
- Абсолютный идеализм Г.В.Ф. Гегеля. Диалектика и принцип системности в философии Гегеля.
Публикации по технике и механике
Публикации по биологии
Публикации по информатике
Публикации по строительству
Публикации по физике
Публикации по химии
Публикации по электронике
Публикации по искусству
Публикации по истории
