Взаимное расположение двух прямых
Рассмотрим две прямые заданные однородными уравнениями.
и : и1 х1+ и2 х2+ и3 х3 =0 и v : v1 х1+ v2 х2+ v3 х3 =0.
Найдем общие точки. Для этого надо решить систему линейных уравнений:
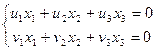 .
.
Из курса алгебры известно, что число линейно-независимых решений однородной системы зависит от ранга матрицы системы и равно число неизвестных минус ранг матрицы.
Пусть r = rg 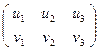 , тогда r
, тогда r 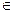 {0, 1, 2}.
{0, 1, 2}.
Случай r = 0 невозможен, так как хотя бы один коэффициент в каждом уравнении отличен от нуля.
Случай r = 1 означает, что строки матрицы пропорциональны, т.е. мы имеем одно и то же уравнение, что означает - прямые совпадают.
При r = 2 , число линейно-независимых решений 3 – 2 = 1, т.е. одно линейно-независимое решение, которое дает одномерное линейное подпространство L1 которое в свою очередь порождает Р0 – проективную точку. Это означает, что прямые пересекаются в одной точке. Других вариантов нет.
Замечание: Тем самым мы доказали, что любые две различные прямые пересекаются в одной точке.
Замечание: Одним из решений однородной системы из двух уравнение от трёх неизвестных будет:
х1= 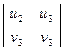 ; х2=
; х2= 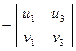 ; х3=
; х3= 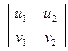 .
.
Вывод:Прямая на проективной плоскости (так же как и точка) определяется набором чисел - и1 , и2 , и3 , с точностью до пропорциональности, которые одновременно не обращаются в ноль.
Определение:Числа ( и1 : и2 : и3 ) называются координатами прямой.
Замечание: Договоримся в дальнейшем записывать координаты точек в виде матрицы-столбца, а координаты прямых в виде матрицы-строки.
Тогда, если Х 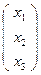 - точка, а и ( и1 и2 и3 ) - прямая, то однородное уравнение прямой можно записать в матричном виде: (и1 и2 и3)∙
- точка, а и ( и1 и2 и3 ) - прямая, то однородное уравнение прямой можно записать в матричном виде: (и1 и2 и3)∙ 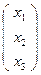 =0 или и∙Х=0.
=0 или и∙Х=0.
Задача. Определить взаимное расположение прямых:
l : 2 х1 - х2+ х3 =0и т : х1+ 3 х2 - 2 х3 =0.
Решение. Координаты прямых будут ( 2 -1 1) и ( 1 3 -2 ) , так как они не пропорциональны, значит прямые различны, а следовательно они пересекаются в одной точке. Найдем эту точку:
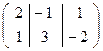 →
→ 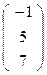 (у второй координаты меняем знак!).
(у второй координаты меняем знак!).
Дата добавления: 2022-02-05; просмотров: 480;











