Координаты точки и уравнение прямой в пространстве
Рассмотрим п –мерное проективное пространство Pп.
Определение: Е1 , Е2 ,…, Еп+1 , Е - упорядоченная система различных точек среди которых никакие три не лежат на одной прямой (Р1), никакие четыре не лежат на одной плоскости (Р2), никакие пять не принадлежат (Р3), и т.д. называется проективным репером в пространстве Pп.
Обозначение:R(Е1, Е2, …, Еп+1, Е) - проективный репер на прямой.
Названия: Е1, Е2,… , Еп+1 - вершины репера или базисные точки,
Е - единичная точка,
(Е1Е2), (Е1Е3), …, (ЕпЕп+1) - координатные прямые.
Проективное пространство Pп порождается Vп+1.
Пусть Е1, Е2,…, Еп+1, Е порождаются - ē1 , ē2 ,…, ēп+1 , ē 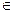 Vп+1.
Vп+1.
Векторы ē1 , ē2 ,…, ēп+1 – линейно независимы (почему?), а значит могут быть базисом в Vп+1.
Определение: Система векторов ē1 , ē2 , ,…, ēп+1 , ē - называется согласованной,
если ē1+ē2 +…+ ēп+1 =ē.
Пусть ē1, ē2, ,…, ēп+1 , ē - согласованная система векторов и пусть точка М 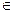 Pп порождается вектором
Pп порождается вектором 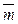 , тогда
, тогда 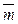 = х1∙ē1+ х2∙ē2 +…+ хп+1 ∙ēп+1
= х1∙ē1+ х2∙ē2 +…+ хп+1 ∙ēп+1
Определение:Набор чисел ( х1 : х2 : … : хп+1 ) называется координатами точки в данном репере.
По аналогии с проективной прямой и проективной плоскостью, координаты точки в Pп определяются с точностью до пропорциональности.
Точки могут лежать на одной прямой или не лежать на одной прямой.
1. А, В, С 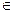 P1 , тогда векторы
P1 , тогда векторы 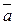 ,
, 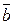 ,
, 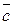
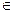 L2
L2 
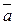 ,
, 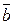 ,
, 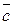 - линейно-зависимы
- линейно-зависимы 
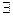 α, β такие, что
α, β такие, что 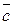 = α∙ā + β∙
= α∙ā + β∙ 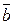

 =α∙
=α∙ 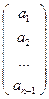 + β∙
+ β∙ 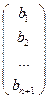 , или rg
, или rg 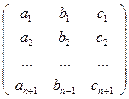 = 2.
= 2.
2. А, В 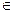 P1 и С
P1 и С 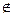 P1 , тогда векторы
P1 , тогда векторы 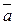 ,
, 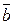 ,
, 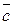
 L2
L2 
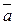 ,
, 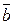 ,
, 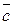 - линейно-независимы
- линейно-независимы 
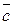 ≠ α∙
≠ α∙ 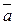 + β∙
+ β∙ 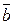

 ≠α∙
≠α∙ 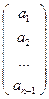 + β∙
+ β∙ 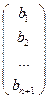 , или rg
, или rg 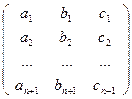 ≠ 2.
≠ 2.
Пусть даны две различные точки А 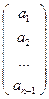 и В
и В 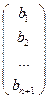 , по свойствам Рп через две различные точки проходит одна и только одна прямая - (АВ).
, по свойствам Рп через две различные точки проходит одна и только одна прямая - (АВ).
Пусть точка Х 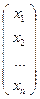
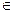 (АВ), тогда
(АВ), тогда 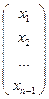 = λ∙
= λ∙ 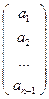 + μ∙
+ μ∙ 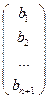 или Х=λ∙А+ μ∙В – параметрическое уравнение прямой в пространстве.
или Х=λ∙А+ μ∙В – параметрическое уравнение прямой в пространстве.
Замечание: В проективном пространстве прямая может задаваться только параметрическим уравнением (сравнить с заданием прямой в евклидовом пространстве).
Однородное уравнение вида и1 х1+ и2 х2+…+ ип+1 хп+1 = 0 не будет задавать прямую.
Дата добавления: 2022-02-05; просмотров: 440;











