Однородные проективные координаты
Рассмотрим расширенную евклидову прямую. Пусть одна из базисных точек будет несобственной, например Е1∞ . Так как на расширенной прямой только одна несобственная точка, то у всех остальных точек х2 ≠0.
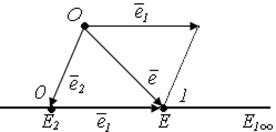 Возьмем базис в V2 следующим образом:
Возьмем базис в V2 следующим образом:
ē = 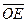 , ē2 =
, ē2 = 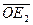 ,
,
тогда ē1 = 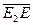 .
.
Пусть М 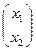

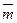 = х1 ∙ē1 + х2 ∙ē2 , или
= х1 ∙ē1 + х2 ∙ē2 , или 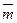 =
= 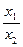 ∙ē1+1∙ē2 =
∙ē1+1∙ē2 = 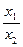 ∙
∙ 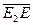 +1∙ē2, но коэффициент 1 перед ē2 будет у всех векторов, кроме ē1, а значит все точки кроме Е1∞ определяются отношением
+1∙ē2, но коэффициент 1 перед ē2 будет у всех векторов, кроме ē1, а значит все точки кроме Е1∞ определяются отношением 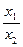 . Если точку Е2 взять в качестве начала отсчета, а точку Е в качестве единицы, то на прямой получается аффинная система координат с базисным вектором ē1=
. Если точку Е2 взять в качестве начала отсчета, а точку Е в качестве единицы, то на прямой получается аффинная система координат с базисным вектором ē1= 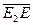 и для построения точки достаточно знать аффинную координату х=
и для построения точки достаточно знать аффинную координату х= 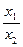 . Единственная точка, у которой не может быть аффинной координаты - точка Е1∞ .
. Единственная точка, у которой не может быть аффинной координаты - точка Е1∞ .
Задача. Найти аффинные координаты точек А 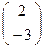 , В
, В 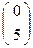 , С
, С 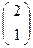
Решение. А 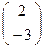 имеет аффинную координату хА= - ⅔,
имеет аффинную координату хА= - ⅔,
В 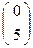 имеет аффинную координату хВ= 0, С
имеет аффинную координату хВ= 0, С 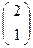 → хС= 2.
→ хС= 2.
Замечание: Если х - аффинная координата точки Х, тогда проективными координатами точки будут - 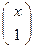 .
.
Точка Е1∞ - не имеет аффинных координат, т.к. её нет на аффинной прямой.
Замечание: Несобственной точкой в репере может быть точка Е2∞ , тогда аффинный репер будет состоять из точек Е1 (начало)и Е (единица), а аффинная координата будет х = 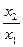 .
.
Определение: Проективный репер прямой, в котором одна из вершин является несобственной точкой называется однородным. (однородная проективная система координат).
Определение: Аффинная система координат, связанная с однородной проективной системой координат называется неоднородной аффинной системой координат.
Замечание: Если несобственной будет единичная точка Е, то репер не будет однородным.
Рассмотрим расширенную евклидову плоскость.
Пусть две базисные точки будут несобственными, например Е1∞ .и Е2∞ .
Если у точки плоскости координата х3 = 0, тогда точка лежит на прямой (Е1∞ Е2∞) которая является несобственной прямой, а значит и сама точка является несобственной.
Рассмотрим точки, для которых х3 ≠ 0.
Возьмем базис в V3 следующим образом: ē= 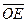 , ē3=
, ē3= 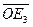 , тогда ē1=
, тогда ē1= 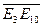 и ē2=
и ē2= 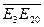 .
.
Пусть М 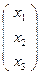 - собственная точка
- собственная точка 
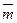 =х1∙ē1+ х2∙ē2+ х3∙ē3, или
=х1∙ē1+ х2∙ē2+ х3∙ē3, или
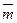 =
= 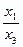 ∙ē1+
∙ē1+ 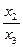 ∙ē2+ ē3=
∙ē2+ ē3= 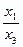 ∙
∙ 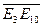 +
+ 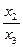 ∙
∙ 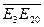 + ē3, но коэффициент 1 перед ē3 будет у всех точек плоскости, для которых х3 ≠ 0, а значит, такие точки определяются отношениями
+ ē3, но коэффициент 1 перед ē3 будет у всех точек плоскости, для которых х3 ≠ 0, а значит, такие точки определяются отношениями 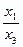 и
и 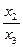 .
.
Если обозначить 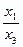 = х и
= х и 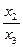 = у, то получим
= у, то получим 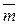 = х ∙ē1 + у ∙ē2 .
= х ∙ē1 + у ∙ē2 .
Это означает, что х и у - аффинные координаты собственных точек на плоскости.
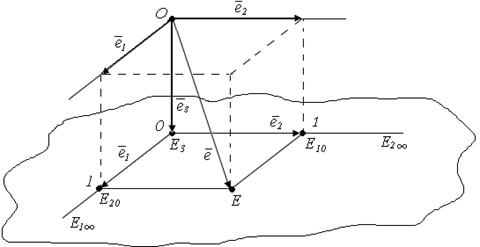
Начало координат в точке Е3 , оси ОХ и ОY - это прямые (Е1∞ Е3) и (Е2∞ Е3), единицы на осях - Е10 и Е20 , базисные векторы ē1 = 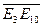 и ē2 =
и ē2 = 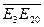 .
.
Вывод: Любая собственная точка М 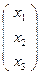 на расширенной евклидовой плоскости будет иметь аффинные координаты - ( х ; у ), где х =
на расширенной евклидовой плоскости будет иметь аффинные координаты - ( х ; у ), где х = 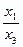 и у =
и у = 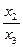 . И наоборот, точка с аффинными координатами - ( х ; у )будет иметь проективные координаты -
. И наоборот, точка с аффинными координатами - ( х ; у )будет иметь проективные координаты - 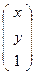 .
.
Если точка несобственная - N∞ , то задать её можно только с помощью прямой на которой она лежит (т.к. каждая прямая имеет только одну несобственную точку).
У всех несобственных точек х3=0, вектор порождающий такую точку будет - 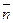 = х1∙ē1+ х2∙ē2+ 0∙ē3 или
= х1∙ē1+ х2∙ē2+ 0∙ē3 или 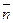 = х1∙ē1+ х2∙ē2 - это направляющий вектор прямой, на которой лежит несобственная точка N∞ .
= х1∙ē1+ х2∙ē2 - это направляющий вектор прямой, на которой лежит несобственная точка N∞ .
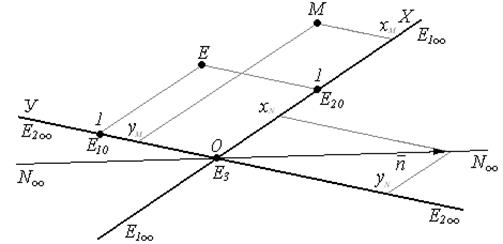
Задача. Найти аффинные координаты точек
А  , В
, В 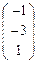 , С
, С 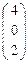 , D
, D 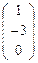 .
.
Решение. Для А  аффинные координаты будут (0,4;-0,6), для точки В
аффинные координаты будут (0,4;-0,6), для точки В 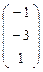 - ( -1 ; -3 ), для С
- ( -1 ; -3 ), для С 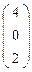 - ( 2 ; 0 ). Точка D
- ( 2 ; 0 ). Точка D 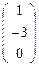 является несобственной, т.к. х3=0 , аффинных координат у этой точки нет. Тогда эту точку можно задать только с помощью прямой на которой она лежит. Направляющий вектор этой прямой будет -
является несобственной, т.к. х3=0 , аффинных координат у этой точки нет. Тогда эту точку можно задать только с помощью прямой на которой она лежит. Направляющий вектор этой прямой будет - 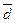 = 1∙ē1 - 3∙ē2 .
= 1∙ē1 - 3∙ē2 .
Задача. Найти проективные координаты точек А( 4 ; -3 ), В( 5 ; 0 ).
Решение. А( 4 ; -3 ) имеет проективные координаты 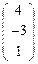 . Точка В( 5 ; 0 ) -
. Точка В( 5 ; 0 ) - 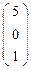 .
.
Задача. Найти координаты несобственной точки, лежащей на прямой т : 2 х + 7 у =0.
Решение. Направляющий вектор прямой будет ( 7 ; -2 )  проективные координаты точки М∞
проективные координаты точки М∞ 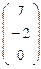 .
.
Замечание: Несобственными точками могут быть точки Е1∞ и Е3∞ , тогда аффинные координаты будут - х = 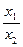 и у =
и у = 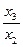 .
.
Или несобственными точками в репере могут быть точки - Е2∞ и Е3∞ (аффинные координаты определите самостоятельно).
Определение: Проективный репер плоскости, в котором две из трёх вершин являются несобственными точками, называется однородным (однородная проективная система координат).
Определение: Аффинная система координат, связанная с однородной проективной системой координат, называется неоднородной аффинной системой координат.
Замечание: Если одной из несобственных точек будет единичная точка Е, то репер не будет однородным.
Дата добавления: 2022-02-05; просмотров: 495;











