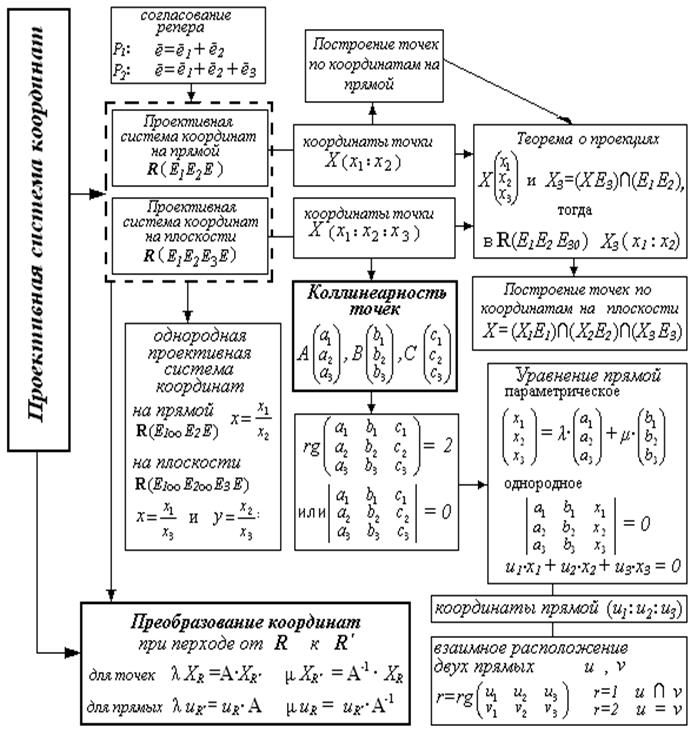
ПРОЕКТИВНАЯ СИСТЕМА КООРДИНАТ
Проективный репер
Рассмотрим проективные прямую P1. и плоскость P2.
Определение: Упорядоченная система из трех различных точек Е1 , Е2 , Е - называется проективным репером на прямой P1.
Обозначение:R(Е1 , Е2 , Е) - проективный репер на прямой.
Определение: Упорядоченная система точек
Е1 , Е2 , Е3 , Е , среди которых никакие три не лежат на одной прямой, называется проективным репером на плоскости.
Обозначение: R(Е1 , Е2 , Е3 , Е) - проективный репер на плоскости.
Названия: Е1 , Е2 , Е3 - вершины репера или базисные точки,
Е - единичная точка,
(Е1Е2), (Е1Е3), (Е2Е3) - координатные прямые.
Пусть R(Е1 , Е2 , Е) - проективный репер на прямой (на P2 все определяется аналогично). P1 порождается V2.
Пусть Е1, Е2 , Е порождаются векторами - ē1 , ē2 , ē 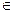 V2.
V2.
Замечание: Так как Е1 ≠Е2  ē1 , ē2 – не коллинеарны, а значит они могут образовывать базис в V2. В дальнейшем будем считать ē1 , ē2 – базисом V2. Аналогично для Р2 - векторы ē1 , ē2 , ē3 – линейно независимы (почему?), а значит могут быть базисом в V3.
ē1 , ē2 – не коллинеарны, а значит они могут образовывать базис в V2. В дальнейшем будем считать ē1 , ē2 – базисом V2. Аналогично для Р2 - векторы ē1 , ē2 , ē3 – линейно независимы (почему?), а значит могут быть базисом в V3.
Определение: Система векторов ē1 , ē2 , ē - называется согласованной, если ē1+ē2=ē (для Р2 - ē= ē1+ ē2+ē3).
Теорема. Всегда существует система векторов согласованная с данным репером.
Доказательство. Докажем для проективной прямой, для проективной плоскости доказывается по аналогии.
Точки Е1 , Е2 , Е порождаются векторами ē1 , ē2 , ē 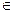 V2
V2  они линейно зависимы
они линейно зависимы 
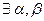 такие, что α∙ē1 + β∙ē2 = ē. Но ē'1=α∙ē1 - порождает точку Е1, а ē'2 =β∙ē2 - точку Е2 (аксиома 2). Тогда система ē'1, ē'2, ē – будет согласованной с данным репером. □
такие, что α∙ē1 + β∙ē2 = ē. Но ē'1=α∙ē1 - порождает точку Е1, а ē'2 =β∙ē2 - точку Е2 (аксиома 2). Тогда система ē'1, ē'2, ē – будет согласованной с данным репером. □
Замечание: Систем векторов согласованных с данным репером много.
Теорема. Пусть R(Е1 , Е2 , Е) репер на прямой, а ē1 , ē2 , ē и ā1 , ā2 , ā - две системы векторов, согласованные с данным репером, тогда 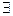 λ ≠ 0 , причем ā1= λ∙ē1 , ā2= λ∙ē2 , ā= λ∙ē.
λ ≠ 0 , причем ā1= λ∙ē1 , ā2= λ∙ē2 , ā= λ∙ē.
Доказательство. Так как вектора ē1 , ē2 , ē и ā1 , ā2 , ā порождают одинаковые точки  по аксиоме 2 они коллинеарны, т.е.ā1=λ1∙ē1 , ā2=λ2∙ē2 , ā=λ∙ē, но системы согласованны
по аксиоме 2 они коллинеарны, т.е.ā1=λ1∙ē1 , ā2=λ2∙ē2 , ā=λ∙ē, но системы согласованны  ē1+ ē2= ē и ā1+ ā2=ā
ē1+ ē2= ē и ā1+ ā2=ā  λ1∙ē1+λ2∙ē2=λ∙ē
λ1∙ē1+λ2∙ē2=λ∙ē  λ1∙ē1+λ2∙ē2=λ∙ē | : λ≠0
λ1∙ē1+λ2∙ē2=λ∙ē | : λ≠0
 ē=
ē= 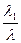 ∙ē1+
∙ē1+ 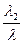 ∙ē2=ē1+ē2
∙ē2=ē1+ē2 
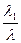 =1 и
=1 и 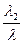 =1
=1
 λ1=λ2=λ
λ1=λ2=λ  ā1=λ∙ē1 , ā2=λ∙ē2 , ā=λ∙ē.
ā1=λ∙ē1 , ā2=λ∙ē2 , ā=λ∙ē.
Для проективной плоскости Р2 рассмотреть самостоятельно (по аналогии). □
Определение: Базисы ē1 , ē2 , ē3 и ā1 , ā2 , ā3, такие, что ēi=λ āi называются гомотетичными.
Дата добавления: 2022-02-05; просмотров: 608;











