Могут ли три координаты точки равняться 0? А две?
Пусть точка Х отлична от вершин репера.
Определение: Проекцией точки Х из Е3 на (Е1Е2) называется точка Х3 такая, что Х3= (ХЕ3)∩(Е1Е2).
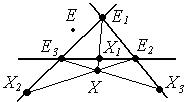
Аналогично определяются проекции из Е2 и Е1:
Х1= (ХЕ1)∩(Е2Е3),
Х2=(ХЕ2)∩(Е1Е3).
Тогда Х= (Х1Е1) ∩ (Х1Е2) ∩ (Х3Е3).
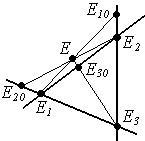
Пусть Е10 , Е20 , Е30. - проекции точки Е на координатные прямые,
тогда на каждой прямой возникает свой репер:
на (Е1Е2) - R(Е1 , Е2 , Е30),
на (Е1Е3) - R(Е1 , Е3 , Е20),
на (Е2Е3) - R(Е2 , Е3 , Е10).
Теорема о проекциях. Пусть R(Е1 , Е2 , Е3 , Е) - репер на проективной плоскости, точка Х 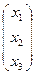 отлична от точек репера, точки Х1 , Х2 , Х3 – проекции точки Х на соответствующие координатные прямые. Тогда
отлична от точек репера, точки Х1 , Х2 , Х3 – проекции точки Х на соответствующие координатные прямые. Тогда
точка Х1 в R(Е2 , Е3 , Е10) будет иметь координаты ( х2 : х3),
точка Х2 в R(Е1 , Е3 , Е20) будет иметь координаты - ( х1 : х3),
точка Х3 в R(Е1 , Е2 , Е30) будет иметь координаты - ( х1 : х2).
Доказательство. Докажем для одной проекции точки, для остальных доказательство по аналогии.
Пусть Х1 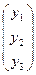 , т.к. Х1
, т.к. Х1 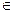 (Е2Е3), тогда у1= 0
(Е2Е3), тогда у1= 0  Х1
Х1 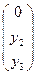 .
.
Точки Х, Х1 , Е1 - принадлежат одной прямой 
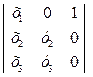 =0
=0  х2∙у3 – х3∙у2=0
х2∙у3 – х3∙у2=0 
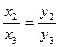
 у2= λ ∙х2 , у3 = λ ∙х3
у2= λ ∙х2 , у3 = λ ∙х3 
Х1 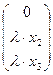 или Х1
или Х1 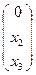 , аналогично: Х2
, аналогично: Х2 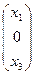 и Х3
и Х3 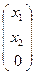 .
.
Тогда проекции точки Е на координатные прямые будут иметь координаты:
Е10 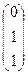 , Е20
, Е20 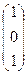 , Е30
, Е30 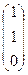 т.к. Е
т.к. Е 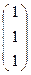 .
.
Рассмотрим: Е10 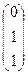 , Е2
, Е2 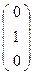 , Е3
, Е3 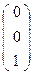 и Х1
и Х1 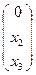 - они все лежат на прямой (Е1Е2).
- они все лежат на прямой (Е1Е2).
Рассмотрим векторы, порождающие эти точки в базисе ē1 , ē2 , ē3 :
ē10 = 0 ∙ ē1 + 1 ∙ ē2 + 1 ∙ē3 , → ē10 = 1 ∙ ē2 + 1 ∙ē3 ,
ē2 = 0 ∙ ē1 + 1 ∙ ē2 + 0 ∙ē3 , → ē2 = 1 ∙ ē2 + 0 ∙ē3 ,
ē3 = 0 ∙ ē1 + 0 ∙ ē2 + 1 ∙ē3 , → ē3 = 0 ∙ ē2 + 1 ∙ē3 ,
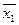 = 0 ∙ ē1 + х2 ∙ ē2 + х3 ∙ē3 , →
= 0 ∙ ē1 + х2 ∙ ē2 + х3 ∙ē3 , → 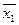 = х2 ∙ ē2 + х3 ∙ē3 .
= х2 ∙ ē2 + х3 ∙ē3 .
Но векторы ē2 , ē3 линейно-независимы, система ē2, ē3 , ē10 - согласована (ē2+ ē3=ē10), а значит точки Е2 , Е3 , Е10 образуют репер R(Е2 , Е3 , Е10 ) и точка Х1 в нем имеет координаты ( х2 : х3). □
Замечание: Это теорема позволяет легко строить точки на проективной плоскости по их проекциям, т.к. Х= (Х1Е1)∩(Х1Е2)∩(Х3Е3).
Дата добавления: 2022-02-05; просмотров: 482;











