Модели проективной прямой, проективной плоскости
1. 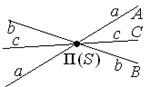 Модель P1 - «пучок прямых» на плоскости П(S).
Модель P1 - «пучок прямых» на плоскости П(S).
Точка S на плоскости – центр пучка.
Прямые пучка – проективные точки.
Пучок прямых – проективная прямая.
2. 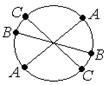 Модель P1 - «окружность».
Модель P1 - «окружность».
Проективными точками являются пары точек –
концы диаметров.
Проективной прямой является окружность.
Определение: Расширенная евклидова прямая – это прямая дополненная одной несобственной (бесконечно-удаленной) точкой.
3. 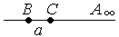 Модель P1 - «расширенная евклидова прямая».
Модель P1 - «расширенная евклидова прямая».
Проективными точками являются: точки прямой – собственные точки,
 и единственная несобственная точка.
и единственная несобственная точка.
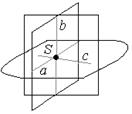
4. Модель P2. – «пучок прямых» в пространстве.
Прямые пучка – проективные точки.
Плоскости пучка – проективные прямые.
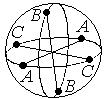
5. Модель P2 - «сфера».
Проективными точками являются пары точек – концы диаметров.
Определение: Расширенная евклидовая плоскость – это плоскость, дополненная несобственной (бесконечно-удаленной) прямой, состоящей из несобственных точек всех прямых лежащих в плоскости.
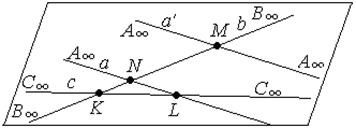
6. Модель P2. – «расширенная евклидова плоскость».
Задача. Докажите что, расширенная евклидова прямая является P1.
Решение. Для доказательства необходимо:
1. Найти V2 – порождающее векторное пространство.
2. Построить отображение, удовлетворяющее аксиомам 1, 2.
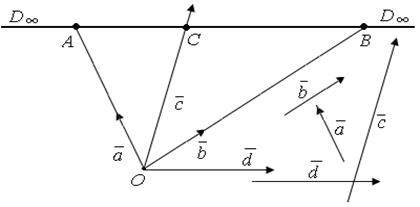
В качестве V2 - берем плоскость, фиксируем базис на плоскости.
Отображение φ: V 02. → P1 зададим: 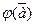 =А,
=А, 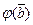 = В,
= В, 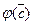 =С,
=С, 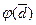 =D∞.
=D∞.
Так как каждая точка на расширенной прямой имеет хотя бы один прообраз – вектор плоскости, то аксиома 1 выполняется.
Так как через точку О можно провести только одну прямую коллинеарную вектору ā, то точка А единственна и все вектора коллинеарные вектору ā будут порождать ту же самую точку А.
Т.о. аксиома 2 выполняется. □
Задача. Докажите, что расширенная плоскость - P2. (самостоятельно).
План: 1. Найти V3 .
2. Построить отображение, удовлетворяющее аксиомам.
Расширенная евклидова прямая и расширенная евклидова плоскость - наиболее наглядные примеры проективной прямой и проективной плоскости.
Свойства несобственных элементов:
1. Любая расширенная прямая имеет единственную несобственную точку.
2. Любая расширенная плоскость имеет единственную несобственную прямую, состоящую из несобственных точек всех прямых, лежащих на этой плоскости.
3. Любые параллельные прямые (в евклидовом смысле) пересекаются в одной несобственной точке.
Свойства P3:
1. Существуют точки общего положения в P3.
а) три точки, не лежащие на одной прямой;
b) четыре точки, не принадлежащие одной плоскости.
Доказательство. P3 порождается V4. Пусть ā1, ā2, ā3, ā4 - базис V4.
φ( ā1 )=А1 , φ( ā2 )=А2 , φ( ā3 )=А3 , φ( ā4 )=А4 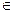 P3 .
P3 .
а) От противного.
Пусть точки А1, А2, А3 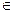 P1 и пусть P1 порождается L2
P1 и пусть P1 порождается L2 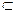 V3, тогда ā1, ā2, ā3
V3, тогда ā1, ā2, ā3 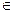 L2
L2  ā1, ā2, ā3 - линейно-зависимы (противоречие). □
ā1, ā2, ā3 - линейно-зависимы (противоречие). □
b) Самостоятельно (от противного, см. (а)).
2. На P2 существует три точки общего положения, т.е. три точки, не лежащие на одной прямой
(самостоятельно).
3. Через любые две различные точки проходит одна и только одна прямая.
Доказательство. Пусть А ≠ В, ā и 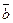 – векторы порождающие эти точки. Тогда ā ≠ α∙
– векторы порождающие эти точки. Тогда ā ≠ α∙ 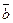
 они линейно-независимы, а значит, могут образовать базис в L2
они линейно-независимы, а значит, могут образовать базис в L2 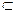 V3 .
V3 .
Подпространство L2 порождает P1, а значит 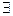 P1 (существование).
P1 (существование).
Пусть 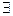 P'1 ≠ P1 , причем А , В
P'1 ≠ P1 , причем А , В 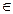 P1 и А , В
P1 и А , В 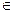 P'1 .
P'1 .
Пусть подпространство L'2 порождает P'1, так как А , В 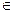 P'1
P'1  ā ,
ā , 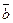
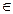 L'2 , но ā ,
L'2 , но ā , 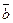
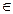 L2
L2  L'2 = L2 (по свойствам линейных подпространств)
L'2 = L2 (по свойствам линейных подпространств)  P'1= P1 (единственность)□
P'1= P1 (единственность)□
4. Через любые три точки не лежащие на одной прямой проходит одна и только одна плоскость.
Доказательство. Самостоятельно (см. (3)).
5. Если две различные точки принадлежат плоскости, то и вся прямая принадлежит плоскости.
Доказательство. Самостоятельно (см. (3)).
6. Любые две различные прямые лежащие в одной плоскости пересекаются в одной точке.
Доказательство. Пусть P'1 ≠ P1 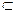 Р2. Пусть пространство V3 порождает P2 , подпространство L2 порождает P1 , а подпространство L'2 порождает P'1 .
Р2. Пусть пространство V3 порождает P2 , подпространство L2 порождает P1 , а подпространство L'2 порождает P'1 .
P1 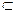 P2
P2  L2
L2 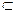 V3 и P'1
V3 и P'1 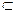 P2
P2  L'2
L'2 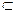 V3 , причем L'2 ≠ L2
V3 , причем L'2 ≠ L2  L'2∩L2=L1
L'2∩L2=L1 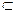 V3 (по свойству подпространств).
V3 (по свойству подпространств).
Таким образом, L1 порождает Р0 - проективную точку, причем Р0 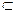 P1 и Р0
P1 и Р0 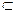 P'1, а значит является точкой пересечения проективных прямых P1 и P'1. Эта точка единственна, иначе противоречие с аксиомой 2. □
P'1, а значит является точкой пересечения проективных прямых P1 и P'1. Эта точка единственна, иначе противоречие с аксиомой 2. □
7. Любые две различные плоскости пересекаются по единственной прямой.
Доказательство. Самостоятельно (см. (6)).
8. Любая плоскость и прямая не принадлежащая этой плоскости пересекаются в одной точке.
Доказательство. Самостоятельно (см. (6)).
Замечание: Любую плоскость в P3 можно рассматривать как проективную плоскость P2.
Изоморфизм моделей
Определение: Две модели называются изоморфными, если существует взаимно-однозначное соответствие между ними, сохраняющее основные отношения между элементами моделей.
Замечание: Основными отношениями между элементами (точками) моделей является отношение «принадлежности».
Для изоморфных моделей в силу взаимной однозначности справедливы сходные утверждения. Это позволяет доказывать утверждения для одной модели и переносить его на другую модель.
Изоморфизм моделей проективной прямой или проективной плоскости доказать самостоятельно (установить биекцию между моделями).
Дата добавления: 2022-02-05; просмотров: 694;











