Цилиндр (прямой, круговой)
Во вспомогательной школе рассматривается только прямой, круговой цилиндр.
При ознакомлении учащихся с понятием цилиндра учитель приносит на урок модели цилиндров различного диаметра, различной высоты, изготовленных из разных материалов, предметы цилиндрической формы; карандаш, стакан, кусок трубы, консервную банку и др. Учитель показывает модель цилиндра, выясняет, знают ли учащиеся название этого геометрического тела, спрашивает, относится ли цилиндр к геометрическим фигурам или телам и почему.
Учащиеся рассматривают модели цилиндров, выделяют и называют верхнее и нижнее основания, боковую поверхность.
Каждый ученик получает модель цилиндра. Учитель просит поставить цилиндр на лист бумаги (сначала одно основание, затем другое) и обвести основания карандашом. Накладывая основания цилиндра на эти круги, учащиеся приходят к выводу, что основания цилиндра — равные круги.
«Если соединить центры кругов — оснований,— говорит учитель,— то получим высоту цилиндра».
Конус (прямой, круговой)
При знакомстве учащихся с конусом учитель демонстрирует различные модели конусов, предметы, имеющие форму конуса (воронка, игрушечная пирамида, бумажный фунтик и т. д.).
Рассматривая модели конуса, дети устанавливают, что основанием конуса является круг. Отделив основание и разрезав боковую поверхность, дети увидят, что боковая поверхность конуса представляет собой часть круга, т. е. сектор.
Пирамида (правильная, полная)
Сначала рассматривается правильная пирамида, в основании которой лежит квадрат.
Учащиеся получают модели пирамид и знакомятся с их элементами. Пирамида имеет основание, боковые грани, ребра, вершины, высоту. Это, например, квадрат (у него все стороны равны, все углы прямые). Боковых граней у такой пирамиды четыре. Учащиеся убеждаются путем измерения, что боковыми гранями являются равнобедренные треугольники, боковые ребра пирамиды равны.
Шар
С этим геометрическим телом учащиеся знакомы с младших классов. В VIII классе их знания о шаре расширяются. Учащиеся узнают о центре шара. Это точка, расстояние от которой до любой точки на поверхности шара одинаково. Радиус шара — это отрезок, соединяющий центр шара с любой точкой поверхности шара. Сечение шара надо показать на модели шара. Однако удобно и даже убедительно показать сечение шара на фруктах или овощах, напоминающих по форме шар.
ПЛОЩАДИ И ОБЪЕМЫ
Площадь
Первое представление о площади геометрических фигур учащиеся получают при рассмотрении и сравнении различных геометрических фигур и установлении между ними отношений больше, меньше, равны.
Ученики знают два способа сравнения отрезков и углов — наложение и измерение сравниваемых фигур. Они имеют также опыт сравнения кругов путем наложения. Теперь следует показать им, как сравнивать различные многоугольники. Например, четырехугольник А больше треугольника Е, так как если их вырезать (учащиеся это должны сделать) и наложить фигуру Е на фигуру А, то она целиком поместится внутри фигуры А. В этом случае говорят: площадь треугольника меньше площади четырехугольника (рис. 44).
Можно предложить сравнить площадь крышки стола и журнала, площадь пола класса и площадь классной доски.
Учащиеся изготавливают к этому уроку различные прямоуголь-

Рис. 44.
ники, круги разных размеров, путем наложения сравнивают их площади, устанавливая отношения больше, меньше, равны.
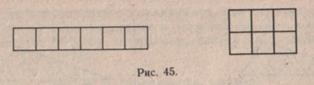
Наконец, учитель предлагает сравнить площади двух равновеликих, но не равных прямоугольников (рис. 45). Сравнение их наложением невозможно (одна фигура не помещается внутри другой и не совмещается с ней). Учитель переворачивает фигуры, и ученики видят, что обратные стороны прямоугольников разделены на одинаковые квадраты. Учащиеся пересчитывают квадраты и делают выводы о равенстве площадей этих прямоугольников. Аналогично сравниваются площади неравновеликих прямоугольников.
Учитель просит сравнить площади, занимаемые окружающими предметами, чтобы развить у ребят глазомер.
Учащимся предлагается сравнить площади знакомых геометрических фигур, вырезанных из клетчатой бумаги. Они пересчитывают число клеточек, которое помещается в каждой фигуре, и сравнивают их количество.
Если фигуры, сравниваемые по площади, будут начерчены на бумаге в клетку, но с разной величиной клеток, подсчет уложившихся в фигурах клеток не позволит выполнить сравнение точно. Поэтому возникает необходимость введения единой меры для измерения и вычисления площади. Можно ввести единицу площади — квадратный сантиметр и познакомить учащихся с нахождением площади прямоугольника путем измерения, а затем и вычисления.
Опыт показывает, что определение площади с помощью мер площади (квадратных мер) целесообразно сравнить с измерением отрезков с помощью мер длины (линейных мер). «В каких единицах выражаются длины отрезков?» — спрашивает учитель. Учащиеся вспоминают единицы мер длины — миллиметр, сантиметр, дециметр, метр. «Можно ли этими единицами измерить площадь?» — задает вопрос учитель. Учащиеся убеждаются, что площадь этими единицами измерить нельзя. Известно, что длина измеряется единицами мер длины, время — единицами мер времени и т. д. Следовательно, площадь должна измеряться единицами мер площади.
Учитель сообщает, что для измерения площади служит площадь квадрата, сторона которого равна 1 см. Площадь такого квадрата называется квадратным сантиметром. Учитель показывает квадратный сантиметр и тут же сравнивает его с линейной мерой —

|
сантиметром. Учащиеся сами должны начертить квадратный сантиметр, вырезать его. Они знакомятся с обозначением этой меры при числах: 1 кв. см. Следует показать и иное обозначение этой меры — 1 см2, с ним они могут встретиться в жизни, на производстве.
Для дифференциации квадратных и линейных мер полезны задания: начертить отрезок длиной 1 см и начертить 1 см2, начертить 2 см2 и два отрезка длиной по 2 см.
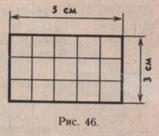
Знакомить учащихся с различными мерами площади сразу не следует, так как они смешивают эти меры, с трудом дифференцируют их. После знакомства с квадратным сантиметром ученики знакомятся с измерениемплощади прямоугольникапутем укладывания квадратных сантиметров и подсчета их (рис. 46). Например, надо измерить площадь прямоугольника ABCD. «Какими единицами мер,— спрашивает учитель,— будем измерять площадь этого прямоугольника? Покажите эти единицы мер площади. Измерять будем так: сначала уложим квадратные сантиметры вдоль нижнего основания. Сколько квадратных сантиметров уложилось в ряду вдоль основания? А какова длина прямоугольника? Обратите внимание, ребята, это очень важно, что квадратных сантиметров по основанию уложилось столько, сколько сантиметров составляет длина прямоугольника. Теперь будем квадратные сантиметры укладывать во второй ряд. Сколько их уложилось во втором ряду? Весь ли прямоугольник заполнен квадратами? Будем заполнять третий ряд. Сколько квадратных сантиметров уложилось в третьем ряду? Сколько всего рядов? Обратите внимание, ребята, что рядов столько же, сколько сантиметров имеет ширина прямоугольника. Подсчитаем, сколько квадратных сантиметров уложилось на всем прямоугольнике. Как их подсчитать?» Таких практических работ должно быть достаточно много. При этом учитель ставит вопросы: «Какова длина прямоугольника? Сколько квадратных сантиметров уложилось вдоль основания? Какова ширина прямоугольника? Сколько рядов квадратных сантиметров уложилось по боковой стороне прямоугольника?»
Полезны упражнения на листе бумаги, расчерченной на квадратные сантиметры. Учащиеся цветными карандашами чертят на этих листах прямоугольники различных размеров, находят их площадь, подсчитывая количество квадратных сантиметров.
Учитель постоянно подчеркивает, что квадратных сантиметров укладывается вдоль основания прямоугольника столько, какова его длина. Рядов укладывается столько, сколько сантиметров составляет ширина прямоугольника.
Далее единицей квадратных мер выкладывается не вся площадь
фигуры: квадратная мера укладывается только вдоль основания, а на смежной стороне отмечается количество рядов. Например, в первом ряду уложилось 6 кв. см (длина прямоугольника б см), а так как ширина его 3 см, то таких рядов будет 3, т. е. должно уложиться 3 ряда по 6 кв. см. Наконец, учащиеся могут не укладывать в основании квадратные сантиметры, а чертить квадратные сантиметры, которые уложатся в основании, и отмечать количество рядов.
Вывод: чтобы определить площадь прямоугольника, надо измерить его длину (определить, сколько квадратных сантиметров уложится в один ряд) и ширину (определить, сколько уложится таких рядов) и эти числа перемножить.
Например, для прямоугольника, длина которого 5 см, а ширина 3 см, площадь (S) вычисляется так: Sпр=5 кв. см х 3, или Sпр = 5 см2 х 3 Sпр= 15 кв. см, Sпр= 15 см2
Очень важно на этом этапе проводить упражнения на дифференциацию понятий периметр и площадь. Например, длина прямоугольника 5 см, ширина 2 см, вычислить его периметр и площадь. Полезно решать задачи, в которых для определения площади прямоугольника (или предмета, имеющего форму прямоугольника) требуется предварительно получить необходимые данные (путем измерения).
Можно устно решить задачи на вычисление длины (ширины) прямоугольника по известной площади и ширине (длине).
После усвоения правила вычисления площади прямоугольникаи проведения упражнений на вычисление площади вводятся новые единицы измерения площади: квадратный дециметр, квадратный метр, квадратный миллиметр, квадратный километр.
Введение каждой новой единицы должно быть обосновано. Учащиеся самостоятельно изготавливают единицы квадратных мер и производят ими измерения. Необходимо развивать глазомер учащихся, определяя площадь сначала на глаз, а затем проверяя точность глазомера путем измерений и вычислений.
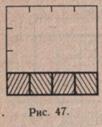
Площадь квадратарассматривается как частный случай площади прямоугольника (рис. 47). Учитель спрашивает у учащихся, как можно найти площадь квадрата. Например, если длина стороны квадрата равна 5 см, то Sкв =5 кв.см х 5 = 25 кв. см, или 5кв = б см2 х 5 = 25 см2.
Более подготовленных учащихся (сверх программы) на уроках или во внеклассной работе по математике можно познакомить с измерением и вычислением площадей других геометрических фигур (параллелограмма, треугольника, круга) и формулами вычисления площадей.
При изучении площади прямоугольника (VIII класс) учитель
 |  |
|
 предлагает обозначить буквой не только площадь (S), но и длину буквой а, ширину буквой Ъ, тогда формула вычисления площади прямоугольникабудет записана так: Sn!,=ab (кв. ед.).
предлагает обозначить буквой не только площадь (S), но и длину буквой а, ширину буквой Ъ, тогда формула вычисления площади прямоугольникабудет записана так: Sn!,=ab (кв. ед.).
Площадь квадрата со стороной а может быть вычислена умножением: Sкв = a х a (кв. ед.), или Sкв = a 2 (кв. ед.).
После знакомства школьников с формулами вычисления периметра и площади сравниваются формулы, порядок выполнения арифметических действий, запись наименований.
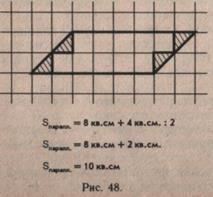
Для расширения знаний учащихся о параллелограмме учитель может вывести формулу вычисления площади параллелограмма.Но сначала дети знакомятся с измерением его площади. Площадь геометрической фигуры учащиеся могут определить, подсчитав количество квадратных мер, которые укладываются на этой фигуре, но это занимает много времени, поэтому используется особое приспособление — палетка-квадрат, разделенный на квадратные сантиметры. Палетку накладывают на фигуру и подсчитывают число полных, а затем неполных квадратов. Число полных квадратов делят пополам и находят общую сумму (рис. 48).
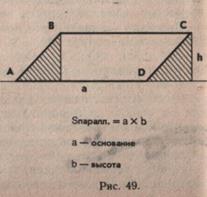
Учащиеся знакомятся с выводом формулы площади параллелограмма. Для этого нужно по высоте параллелограмма отрезать треугольник и приставить его с другой стороны для преобразования параллелограмма в его частный вид — прямоугольник (рис. 49). Чертеж следует делать после работы с моделью. Площадь данного параллелограмма равна площади прямоугольника с такими же основанием и высотой, как у параллелограмма, и, следовательно, равна произведению длины основания и его высоты. Для большей убедительности нужно сравнить результаты вычисления площади по формуле 5паралл=а-А (а — основание, h — высота) с площадью, вычисленной с помощью палетки.
|
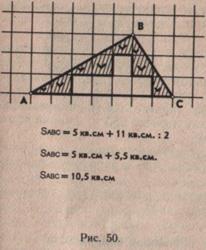
Площадь треугольникасначала находится с помощью палетки (рис. 50). Для вывода формулы учитель предлагает взять парал-
|
Вначале площадь кругаучащиеся измеряют с помощью палетки (рис. 51). Для вывода формулы площади круга предлагается разрезать 4 круга разных радиусов: первый на 4, второй на 8, третий на 16, четвертый на 32 равных сектора. Секторы каждого круга надо наклеить в тетрадь так, как показано на рисунке 52, т. е. один сектор дугой вверх, следующий — дугой вниз, чтобы радиусы совпали.
При увеличении числа секторов, на которые разбивается круг, получающиеся фигуры по форме все более приближаются к прямоугольнику. Если бы мы продолжили деление круга на секторы и дальше, то получили бы прямоугольник с основанием, равным половине длины окружности, и высотой, равной ее радиусу. Учащиеся знают, что длина окружности равна 2pг, где p » 3,14.
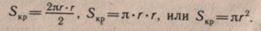
Дата добавления: 2022-02-05; просмотров: 575;












