ЗАДАЧИ ГЕОМЕТРИЧЕСКОГО СОДЕРЖАНИЯ

В связи с тем что геометрический материал во вспомогательной школе тесно связан с арифметическим, то задачи геометрического содержания должны быть направлены как на формирование и закреп­ление геометрических представлений и понятий, вычерчивание и построение геометрических фигур, формирование чертежных, графи­ческих и измерительных навыков, так и на закрепление арифме­тических знаний. Решение задач геометрического содержания позво­ляет теснее увязать изучение геометрического и закрепление ариф­метического материала на уроках математики.

Анализ программы и учебников математики для учащихся вспо­могательной школы показывает, что они содержат систему геомет­рических задач для закрепления теоретических знаний по наглядной геометрии, а также для формирования умений и навыков по черче­нию, моделированию, измерению и др.

Эта система включает: 1) задачи на узнавание, выделение гео­метрических фигур и их элементов; 2) задачи на измерение; 3) за­дачи на вычерчивание и построение геометрических фигур; 4) задачи на классификацию геометрических фигур; 5) задачи на сравнение геометрических фигур; 6) задачи на видоизменение фигур (деление на части, составление одних фигур из других); 7) задачи на вычисление и построение геометрических фигур.

1) Задачи на узнавание, выделение геометрических фигур и тел и их элементов.

Знакомство с геометрическими фигурами и телами начинается с их узнавания, называния и различения. Учащиеся знакомятся с геометрическими фигурами и телами различной формы (кругом, ша­ром, квадратом, кубом, треугольником, прямоугольником, брус­ком), учатся их узнавать, выделять среди других (по внешнему виду).

Сначала перед учениками ставится задача найти такую же фи­гуру (или тело) — среди множества фигур учащиеся должны уз­нать фигуру, одинаковую с данной по форме, цвету, размерам. Они запоминают названия этих фигур, обводят их на листе бумаги, чертят «от руки».

Затем перед учащимися ставится более трудная задача: из мно­жества фигур (или тел) выделить фигуру (тело), одинаковую с данной по форме, например отобрать все треугольники. В этом случае учащиеся должны отвлечься от несущественных признаков фигур, а учитывать только существенный признак. Узнавание фигур уча­щимися происходит как на моделях, так и на чертежах.

Начиная со II класса учащиеся решают задачи на выделение в фигурах различных элементов: сторон, углов, вершин. Учащиеся знакомятся с задачами такого содержания: «Покажите и сосчитайте углы (стороны, вершины) данной фигуры. Сосчитайте углы в много­угольнике и скажите, как называется этот многоугольник».

Решение задач такого вида сопровождается непосредственным показом, рассмотрением моделей геометрических фигур, чертежей, выделением на них элементов (углов, вершин, сторон). Можно также выделить цветом отрезки, образующие отдельные фигуры.

Задачи вида «В многоугольнике 6 углов. Как называется такой многоугольник? Представьте себе восьмиугольник. Сколько углов, вершин, сторон в восьмиугольнике?» могут решаться без исполь­зования пособий: их цель — развивать воображение учащихся. Од­нако для проверки правильности решения целесообразно показать модели фигур.

Наряду с уже известными геометрическими фигурами учащиеся

узнают углы: прямой, больше прямого, меньше прямого. Затем они учатся называть углы: острые, прямые, тупые. Узнавание углов происходит сначала «на глаз», а затем с помощью чертежного тре­угольника путем наложения его на модель или чертеж.

В VII классе узнавание углов и их различение по величине уча­щиеся выполняют с помощью транспортира. Решаются задачи та­кого содержания: «На чертеже назвать и показать сначала острые, затем прямые и тупые углы (на чертеже даны все виды углов, они либо пронумерованы, либо обозначены буквами). Назвать и пока­зать тупые углы в пятиугольнике (учащимся предлагается модель или чертеж пятиугольника, и они должны с помощью чертежного треугольника или транспортира измерить углы, определив их виды, назвать и показать тупые углы многоугольника)».

В VII классе учащиеся, наряду с прямыми, острыми и тупы­ми углами, учатся узнавать и выделять развернутые, полные, смеж­ные углы.

Во всех классах вспомогательной школы учащиеся учатся на­ходить указанную фигуру на чертеже. Например, определить, сколько треугольников возможно выделить на чертеже (рис. 58), сколько на этом чертеже прямоугольников (рис. 59).

Для решения задач такого вида учитель вначале помогает уча­щимся отыскать фигуры на чертеже, закрывая его части. В этом случае искомые фигуры выделяются рельефнее. Этим способом постепенно учатся пользоваться ученики сами. В результате разви­вается наблюдательность, воображение учащихся.

В VIII классе проводится большая работа с моделями любого прямоугольного параллелепипеда и их развертками. Рассматривая отдельные детали развертки, учащиеся определяют (узнают) гео­метрическое тело.

2) Задачи на измерение.

В I классе учащиеся получают представление о длине, учатся сравнивать отрезки наложением, приложением, «на глаз», а затем знакомятся и с их измерением с помощью единицы измерения дли­ны — сантиметра (см. с. 50). В этот период они решают задачи на измерение заданных геометрических отрезков, а также на вы­черчивание отрезков по заданным размерам.

При решении задач на измерение отрезков учитель должен по­знакомить учащихся с устройством линейки и правилами пользова-136

ния ею. Во II классе она представляет собой полоску длиной 10 см, разделенную на 10 равных частей.

Учащиеся II класса решают задачи на измерение с помощью этой линейки, далее они пользуются обычной ученической линейкой. Учитель знакомит учеников с задачами: измерить полоску, записать реультат измерения; измерить две полоски и определить, которая из них длиннее. На первых порах измерение проводится учащимися под руководством и с помощью учителя. Учащиеся должны не только измерять отрезки, но и подробно рассказывать при этом о своей практической деятельности. Вначале учитель наводящими вопросами помогает детям: «Каким инструментом измеряются от­резки? Каким штрихом надо приложить линейку к началу полоски? Что можно узнать, посмотрев на конец полоски? Какова длина полоски? Запишите это число». Затем ученики самостоятельно долж­ны рассказать, как выполняли измерение.

Во II, III, IV классах измерения выполняются в сантиметрах, в дециметрах или в метрах, в V классе — в миллиметрах.

Начиная с IIIкласса измерения производятся не только одной, но и двумя мерами длины: например, в метрах и дециметрах или в сантиметрах и миллиметрах. Результат измерения в этом случае запи­сывается числом с двумя наименованиями мер. Например, длина парты равна 1 м 25 см.

При измерении отрезка может быть использован циркуль в ка­честве измерителя. Учащиеся устанавливают ножку циркуля в точ­ку — начало отрезка, его грифель — в конец отрезка. А затем пере­носят циркуль, не меняя его раствора, на линейку: ставят острые ножки циркуля на нулевой штрих линейки, длина отрезка опре­деляется тем штрихом линейки, с которым совпадает грифель. Для развития глазомера перед выполнением измерений дети называют предполагаемую длину полоски, отрезка и т. д. Измерение служит проверкой высказанных предположений.

Учащиеся младших классов решают задачи на измерение эле­ментов геометрических фигур, например на измерение сторон, ре­бер, отрезков ломаных линий. Даются задания: «Измерить осно­вания и боковые стороны прямоугольника. Измерить стороны квадра­та.» При решении этих задач необходимо спросить у учащихся: «Сколько измерений надо сделать? Почему? Какую единицу изме­рения надо выбрать?»

Задачи на измерение включают и задачи на измерение величин углов, например: «Измерьте угол и определите, какой это угол по виду. Измерьте углы в треугольнике. Измерьте один угол фигуры». И т. д.

Для решения задач такого вида учащиеся должны иметь пред­ставление о единицах измерения углов и уметь пользоваться тран­спортиром для измерения величин углов.

Готовя учащихся к решению таких задач, учитель должен уделять достаточное внимание формированию правильных навыков использования транспортира при измерении углов. Учащиеся рабо­тают на первых порах под непосредственным руководством учи

1.17

теля. Они должны научиться не просто правильно пользоваться транспортиром, но и сопровождать свою деятельность словесными пояснениями.

К задачам на измерение относятся также задачи на измерение площадей и объемов (см. с. 120).

При решении геометрических задач на измерение от учащихся требуется достаточно хорошая точность измерения, правильное ис­пользование измерительных инструментов. Следовательно, при ре­шении задач на измерение учитель должен проводить большую индивидуальную работу с каждым учеником класса. Это необходимо для того, чтобы привести детей от знания того, как использовать измерительные инструменты, к выработке прочных автоматизиро­ванных навыков измерения. В условиях вспомогательной школы выработать такие навыки можно лишь ежедневной систематической работой каждого ученика класса с измерительными инструментами. Сначала учитель оказывает непосредственную помощь ученикам, а затем степень помощи уменьшается, и, наконец, ученики само­стоятельно выполняют работу.

3) Задачи на вычерчивание и построение геометрических фигур.

Задачи данного вида решаются на каждом году обучения во вспомогательной школе.

В I классе учащиеся знакомятся с решением задач на вычерчи­вание отрезков по точкам (соединить две точки отрезком).

Во II классе дети вычерчивают квадраты, любые прямоуголь­ники, треугольники сначала от руки, а затем с помощью линейки по заданным точкам (вершинам).

Учитель заранее готовит лист плотной бумаги, на котором дети будут выполнять чертеж, ставит на нем точки и просит учащихся с помощью линейки соединить их так, чтобы получился: отрезок, если даны 2 точки (его концы); квадрат или другого вида прямо­угольник, если даны 4 точки (вершины); треугольник, если даны 3 точки. Учащиеся, вычертив фигуру, должны назвать ее, назвать элементы фигуры, их количество.

При вычерчивании геометрических фигур учитель учит детей правильно держать линейку, карандаш, не нажимать сильно каран­дашом на бумагу при проведении прямых и отрезков, не двигать лист бумаги, а менять положение только линейки. Учитель следит за точностью построения отрезков заданной длины.

С IV класса учащиеся решают более трудные задачи на построе­ние. Они вычерчивают с помощью линейки и чертежного треуголь­ника прямоугольники (квадраты) по заданным размерам, параллеле­пипеды (ромбы), треугольники, ломаные линии, шестиугольники, углы, окружности (круги), учатся складывать и вычитать отрезки, т. е. находить их сумму и разность или остаток.

Наряду с этим они должны учиться строить фигуры, равные данной. Например: построить отрезок, равный данному, построить квадрат (треугольник, ромб, шестиугольник), равный данному, по-

строить развертку куба (параллелепипеда, пирамиды), равную дан­ной, и т.д.

Выясняется, какие данные надо иметь, чтобы построить прямо­угольник, равный данному, с помощью циркуля, линейки и чертеж­ного треугольника (предъявляется чертеж или модель прямоуголь­ника). Затем уточняется, как эти данные получить. Когда уча­щиеся вспомнят, что для построения прямоугольника надо знать его длину и ширину, учитель предлагает измерить длину и ширину данного прямоугольника. Далее построение выполняется известным ученикам способом.

Решение задач такого вида опирается не только на измеритель­ные и чертежные умения и навыки. Необходима актуализация имеющихся у учащихся знаний (построение фигуры, равной данной, возможно лишь при том условии, если ученик четко понимает, наличие каких данных позволяет построить эту фигуру). Например, чтобы построить квадрат, равный данному, достаточно измерить только одну его сторону и уметь строить прямые углы. Для построе­ния треугольника, равного данному нужно знать (измерить) длину трех его сторон, или длину двух сторон и величину угла, заклю­ченного между ними, или длину одной стороны и величину двух углов, прилежащих к ней.

Решение этого вида задач целесообразно начинать с решения таких, в условиях которых прямо сказано, какие измерения надо произвести, прежде чем приступить к построению фигуры, равной данной. Например: «Измерь основание и боковую сторону прямо­угольника и начерти такой же в тетради. Измерь длину и ширину прямоугольника и начерти такой же». А затем уже можно переходить к решению задач, в условии которых не сказано, какие измерения надо производить для построения фигуры, равной данной.

Для закрепления способов решения задач данного вида целесо­образно требовать от учащихся обоснования правильности постро­ения фигуры и соответствия полученной фигуры заданным в условии задачи параметрам. Например, в выше сформулированной задаче они должны показать, что полученная фигура — прямоугольник задан­ных размеров. С этой целью они должны измерить углы, противо­положные стороны и установить, что углы у полученного четырех­угольника прямые, длина основания 5 см, а длина боковой сторо­ны 3 см, т. е. установить, что размеры полученного прямоугольника соответствуют тем числам, которые даны в условии.

4) Задачи на классификацию геометрических фигур.

Знание свойств геометрических фигур, умение их узнавать, вла­дение геометрической терминологией создают предпосылки для реше­ния задач на классификацию. Важно такие задачи подобрать с учетом возрастающей трудности.

Уже в I классе, еще не зная свойств фигур, а различая их лишь по внешнему виду, учащиеся могут из множества фигур отобрать нес круги, затем все квадраты, все треугольники, шары

и т. д. Причем, проводя такую классификацию фигур, учащиеся опираются на один существенный признак — форму, отвлекаясь от несущественных признаков (цвета, размера, материала и др.).

Во II классе они решают задачи на классификацию углов.

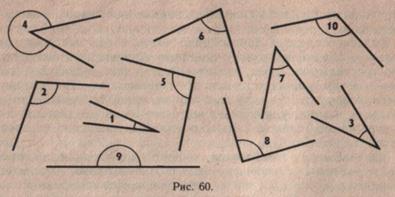
Например, учитель предъявляет плакат с чертежами углов разных видов (рис. 60).

Учащиеся должны определить вид углов с помощью чертежного треугольника, а затем назвать устно или записать номера всех острых, тупых и прямых углов.

Острые углы — 1, 5, 8, 9.

Тупые углы — 3, 4, 6.

Прямые углы — 2, 7, 10.

Аналогичные задачи на классификацию решаются с различными видами линий, многоугольников (рис. 61). Например: «Обозначьте красной звездочкой все замкнутые линии, а синей — незамкнутые. Отберите (назовите, если треугольники обозначены буквами или цифрами) все прямоугольные (равнобедренные) треугольники. По­кажите и назовите все четырехугольники. Из четырехугольников назовите только квадраты (параллелограммы)». И т. д.

При решении данных задач учащиеся должны рассмотреть осо­бенности не только фигур в целом, но и свойства элементов данной

фигуры, сравнить их со свойствами аналогичных элементов других фигур, найти в них общее и различное и на основании этого сравне­ния произвести классификацию. Так, выясняя, является ли данный треугольник прямоугольным, учащиеся должны устанавливать ве­личину всех углов в треугольнике (если в треугольнике один из углов — прямой, то такой треугольник относится к прямоугольным). Выясняя, является ли данный четырехугольник квадратом, уче­ники должны определить величину всех углов и длины его сторон и установить, что в данном четырехугольнике все углы прямые, а стороны равны.

Для умственно отсталых школьников даже самые простые за­дачи на классификацию представляют значительные трудности, так как рассуждения строятся на необходимости выделения сущест­венных признаков, отвлечения от несущественных, установления причинно-следственных связей и отношений, установления видовой и родовой иерархии.

5) Задачи на сравнение геометрических фигур.

Задачи на классификацию тесно связаны с задачами на сравне­ние, так как классификацию невозможно осуществить, не сравнивая одну фигуру с другой.

Сравнению геометрических фигур и тел во вспомогательной школе необходимо учить, так как психологические исследования показывают, что умственно отсталые школьники нередко производят сравнение не по соотносимым признакам, учитывают не все су­щественные признаки.

При сравнении фигур следует приучить учащихся руководство­ваться определенным порядком:

1) установить количество элементов фигур (например, число углов, сторон, вершин);

2) установить соотношение углов сравниваемых фигур;

3) установить соотношение сторон фигур.

Для сравнения элементов фигур учащиеся пользуются измери­тельными инструментами: для измерения сторон — линейкой (можно использовать и мерку — полоску бумаги), циркулем; для измерения величины углов — чертежным треугольником, транспортиром.

Учащиеся не только решают задачи на сравнение фигур, но сравнивают и такие геометрические понятия, как периметр, пло­щадь, объем, которые ими усваиваются с большим трудом и слабо дифференцируются. Сравниваются и задачи на измерение и вычисле­ние периметра, площади, объема. («Что такое периметр, площадь, объем? Какие используются формулы для вычисления периметра, площади, объема?»)

6) Задачи на видоизменение фигур.

Задачи данного вида имеют значение не только для закрепления знаний о свойствах геометрических фигур, но и для развития ком­бинаторных способностей учащихся, их внимания, наблюдатель-

ности, сообразительности, воображения, творческого мышления.

Самые простые задачи на видоизменение фигур можно предъ­являть учащимся уже в I классе вспомогательной школы.

Например, с помощью палочек учитель выкладывает квадрат, а затем предлагает из этих палочек сложить треугольник. Затем спрашивает: «Сколько палочек надо убрать? Как положить остав­шиеся палочки?» Или, например, даются задачи:

Начертить прямую линию, поставить на ней точку; показать полученные лучи, сказать, сколько получено лучей. Сколько точек нужно изобразить, чтобы получить один или два отрезка?

Во II классе возможности решения задач на видоизменение фигур увеличиваются, так как учащиеся знакомятся с углами, элементами фигур.

Например, предлагаются такие задачи:

С помощью палочек образован угол. Сколько палочек надо добавить, чтобы получить треугольник (квадрат)?

Как из квадрата (прямоугольника) получить два треугольника?

Измерь основание и боковую сторону прямоугольника (рис. 62). Что надо изменить в данном прямоугольнике, чтобы сделать из него квадрат?

Сколько можно получить квадратов из данного прямоугольни­ка (рис. 63)?

Приведем примеры задач на видоизменение фигур.

1) В данном многоугольнике провести отрезки так, чтобы полу­чилось три квадрата (рис. 53).

2) Достроить данную фигуру до треугольника (рис. 64 и 65).

3) В данной фигуре провести отрезок так, чтобы образовался квадрат (рис. 66).

4) Из палочек сложить равнобедренный треугольник. Что нужно сделать, чтобы этот треугольник стал равносторонним (разносторон­ним)?

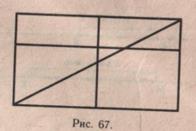
5) В данном прямоугольнике проведи отрезок так, чтобы получи­лось два равных треугольника, два квадрата, два равных прямо­угольника (рис. 67).

7) Задачи на вычисление и построение.

Во всех классах вспомогательной школы решаются задачи гео­метрического содержания, тесно связанные с арифметическим ма­териалом, целью которых является уточнение, закрепление матема­тических знаний, использование их в новых ситуациях.

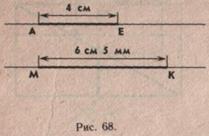
Например, учащиеся знакомы с понятием увеличения и умень­шения числа на несколько единиц. Закрепление этого понятия происходит при решении задач геометрического содержания. Напри­мер: длина отрезка АЕ равна 4 см. Отрезок МК длиннее на 2 см 5 мм. Вычислить длину отрезка МК. Начертить оба отрезка.

В данной задаче и задачах, аналогичных ей, т. е. таких, где задана длина одного отрезка или одной из сторон геометрической фигуры, а длина другого отрезка или стороны неизвестна, но сказано, что она на несколько единиц или в несколько раз длиннее или короче данной, необходимо сначала произвести вычисления, т. е. решить арифметическую задачу, а затем выполнить построение. Подводя учащихся к решению задачи, учитель ставит вопросы, требующие от учащихся актуализации знаний, необходимых для решения задач на увеличение и уменьшение числа на несколько единиц. Учащиеся вспоминают, каким действием решаются такие задачи. Производится вычисление. После того как установлена длина второго отрезка, выполняется построение (рис. 68).

При решении задач на вычисление и построение важно вырабо­тать у учащихся прочный навык в оформлении записи задачи. Опыт показывает, что при решении задач данного вида целесообраз­но использовать такую форму записи:

Задача.

Дано: Построить:

АЕ – 4 см отрезки АЕ и МК

МК — ? — на 2 см 5 мм длиннее

Решение.

1) МК=4 см +2 см 5 мм МК=6 см 5 мм

Построение.

Приведем еще один пример решения задачи геометрического содержания на вычисление и построение.

Построить прямоугольник ABCD, у которого основание AD = 4 см, а боковая сторона АВ на 5 мм короче (рис. 69).

Задача.

Дано: Решение.

AD — 4 см 1) АВ=4 см - 5 мм

АВ – ? – на 5 мм короче АВ = 3 см 5 мм

Построить: прямоугольник ABCD

Построение.

В IV классе, когда учащиеся получают понятие о ломаной ли­нии, о длине ломаной линии, закрепление знаний происходит при решении задач на вычисление и построение.

Например: начертить ломаную линию, которая состоит из трех отрезков длиной 3 см, 4 см, 2 см, вычислить длину ломаной.

При разборе данной задачи учитель объясняет, что сначала надо выполнить построение ломаной линии с заданной длиной от­резков. Обращается внимание на то, что положение отрезков произ­вольное. Далее учитель спрашивает, как вычислить длину ломаной. Учащиеся вспоминают, что длина ломаной — это сумма длин ее от­резков (нужно выполнить сложение чисел 3 см, 4 см, 2 см, полученное число 9 см и есть длина ломаной). Проверка правильности реше­ния может быть произведена путем последовательного откладыва­ния трех отрезков — звеньев ломаной на прямой и измерения по­лученного отрезка — суммы.

Решение задач на вычисление, которые были рассмотрены выше, опиралось на наглядную основу.

Во вспомогательной школе в старших классах находит широкое применение решение задач на вычисление. Начиная с VI класса решаются задачи на вычисление периметра геометрических фигур различной формы: квадрата, треугольника, прямоугольника, ромба, параллелограмма.

144

ЛИТЕРАТУРА

Головина Т. Н. Изобразительная деятельность учащихся вспомогательной школы.—М., 1974. Киселев А. П. Элементарная геометрия.—М., 1980.

М а т а с о в Ю. Т. Особенности восприятия и понимания основ наглядной геометрии учениками младших классов вспомогательной школы // Дефектология.— 1972.— № 5.

Моро М. И., П ы ш к а л о А. М. Методика обучения матема­тике в I — III классах.— М., 1978.

Н е ш к о в К. И., П ы ш к а л о А. М. Математика в начальных классах.—М., 1968.—Ч. I.

Перова М. Н. Дидактические игры и занимательные упраж­нения на уроках математики во вспомогательной школе.—М., 1976.

Перова М. Н. Методика преподавания математики во вспо­могательной школе.— М., 1989.

П е р о в а М. Н., Э к В. В. Изучение взаимного положения гео­метрических фигур на плоскости на уроках математики во вспо­могательной школе//Дефектология.—1982.—№ 1.

Обучение учащихся I—IV классов вспомогательной школы / Под ред. В. Г. Петровой.—М., 1982.—Ч. I.

Пышкало А. М. Методика обучения элементам геометрии в начальных классах.—М., 1973.

Эк В. В. О преемственности некоторых вопросов геометрии во вспомогательной школе//Дефектология.— 1977.— № 6.