Измерение и построение ломаной линии

К измерению ломаной линии, определению ее длины учащиеся подготовлены предшествующим опытом, так как начиная со II клас­са они чертили произвольные отрезки, измеряли отрезки одной и двумя мерами длины, записывали результаты измерения числами с наименованиями, чертили отрезки заданной длины.

В V классе учащиеся знакомятся с измерением ломаной линии и миллиметрах, сантиметрах, дециметрах, метрах, а также в двух мерах, например в сантиметрах и миллиметрах. На моделях ломаной линии или чертежах учащимся предлагается измерить отрезки ло­маной линии, предварительно оговорив целесообразность выбора меры измерения. На первых порах учитель может дать задание про­извести измерение отрезков ломаной линии в определенных мерах длины (сантиметрах, миллиметрах и др.).

Результат измерения каждого отрезка записывается на модели, на чертеже. Например, если на чертеже изображена незамкнутая ломаная линия ABCD, то ученики, измерив длину ее отрезков в сан­тиметрах, должны написать: АВ = ... см, ВС = ... см, CD = ... см. За­тем учитель предлагает сложить длины отрезков этой ломаной и сообщает учащимся, что они получили длину ломаной линии.

Предлагается такая запись:

ABCD=AB + BC + CD

ABCD = ... см + ... см + ... см ABCD = ... см

Учитель сообщает учащимся, что длину ломаной линии можно определить, не измеряя длины каждого из ее отрезков, а последова­тельно откладывая с помощью циркуля их на произвольной прямой

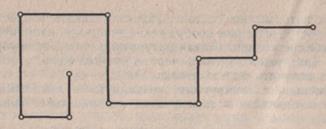
Рис. 4.

от произвольной точки, измерить получившийся отрезок, равный сумме звеньев ломаной.

Например, дана незамкнутая ломаная линия MNOPK- Алгоритм построения отрезка, равного длине ломаной MNOPK, состоит из следующих этапов:

1. Построить произвольную прямую.

2. На прямой отметить точку М.

3. С помощью циркуля измерить отрезок MN ломаной линии.

4. От точки М отложить отрезок MN на произвольной прямой.

5. Также последовательно с помощью циркуля на прямой отло­жить отрезки NO, OP, PK.

6. Отрезок МК равен длине ломаной MNOPK-

Проверить,что МК — длина ломаной MNOPK, можно путем из­мерения отрезков ломаной и сложения длин отрезков. Длина МК и сумма длин отрезков ломаной MNOPK совпадают. Такой способ нахождения длины ломаной назовем геометрическим.

Построение ломаной линии включает в себя вычерчивание от­резков данной длины, вычерчивание отрезков по образцу. Задания могут быть следующих видов:

1) Начертить в тетрадях незамкнутую ломаную по образцу.
Получив карточку с изображением ломаной линии, учащиеся

строят в тетради свою ломаную, перенося в тетрадь отрезки-звенья с помощью измерителя (циркуля) или измеряя и строя их с помощью линейки.

Углы между звеньями могут совпадать с углами на образце толь­ко приблизительно. Вид углов должен сохраниться.

2) Вычертить в тетрадях ломаную линию, равную данной (рис. 4).
Это возможно на данном этапе, если отрезки ломаной линии

даны под прямыми углами (для построения углов используется чер­тежный треугольник).

3) Вычертить в тетради ломаную линию по данной длине отрез­ков (указывается вид углов, образованных отрезками ломаной).

4) Вычертить ломаную линию, если дана ее длина и указано чис­ло отрезков (длина каждого отдельного отрезка выбирается произ­вольно с учетом заданных условий, в отдельных случаях может быть дано указание, что отрезки равны).

Каждое из заданий сначала выполняется под руководством учи­теля в ходе фронтальной работы с классом, а потом включается в самостоятельную работу школьников.

Навык измерения ломаной может быть сформирован с помощью следующих заданий:

1) Измерить каждый отрезок заданной ломаной (ломаная дана на карточке), вычислить сумму длин всех отрезков.

2) Измерить расстояние между концами незамкнутой ломаной, чтобы определить длину «недостающего» отрезка.

3) Вычертить произвольную замкнутую ломаную линию, целиком находящуюся внутри заданной фигуры (круга, квадрата, любого прямоугольника, размеры которых даны), и найти ее длину.

На следующем году обучения (в VI классе) работа с линиями продолжается: идет классификация и дифференциация линий. Необ­ходимо разнообразить взаимное положение линий на плоскости, их расположение по отношению к краям тетради.