Горизонтальное, вертикальное и наклонное положения прямой в пространстве

В VI классе рассматривается различное положение прямой, плос­ких фигур в пространстве по отношению к горизонту (в это же время учащиеся изучают направления на уроках географии). Понятие о горизонтальном положении целесообразно дать, рассматривая кар­тину с изображением пейзажа с линией горизонта. Надо провести экскурсию в открытое поле с целью увидеть линию горизонта в при­роде. Учащиеся вспоминают, что такое горизонт. Учитель показы­вает прямую в горизонтальном положении (палку, рейку держит горизонтально).

Горизонтальное положение плоскости можно показать, демон­стрируя горизонтальную поверхность жидкости. В прозрачный со­суд наливают подкрашенную воду, бросают на поверхность листок бумаги, картона. Сосуду придают разные положения, а поверхность воды в нем занимает только горизонтальное положение.

Далее учитель знакомит учащихся с прибором для определения горизонтального положения — уровнем, рассказывает о его устройстве и правилах использования. С помощью уровня, выполняя практическую работу, учащиеся учатся определять горизонтальное поло­жение прямых, плоских поверхностей предметов, находящихся вокруг (их. Если положение прямой или поверхности того или иного пред­мета не горизонтально, то оно может быть либо наклонным (учитель показывает прямые в наклонном положении), либо вертикальным. Прямая линия (рейка) располагается под прямым углом к линии горизонта или линии в горизонтальном положении. Эта рейка, говорит учитель, находится в вертикальном положении. Учащиеся на­ходит планки, рейки и другие предметы в окружающей обстановке, положение которых вертикально. Учитель показывает и описывает прибор (отвес) для определения вертикального положения и предла­гает каждому ученику изготовить его. Затем с помощью отвеса уча­щиеся определяют направления (положения) отдельных прямых ли­ний, предметов.

Далее проводятся упражнения на дифференциацию прямых, имеющих горизонтальное, вертикальное и наклонное положения.

Можно провести игру-соревнование «Кто больше назовет пред­метов, находящихся в горизонтальном, наклонном и вертикальном положениях?». Соревнуются три ученика. Каждый должен назвать нe менее десяти предметов и с помощью соответствующего прибора доказать правильность своего ответа, т. е. проверить положение и рассказать, как он это делает.

Взаимное положение прямых на плоскости.

Перпендикулярные и параллельные прямые,

Их построение

До изучения перпендикулярных и параллельных прямых школьники должны получить понятие о пересекающихся и непересекаю­щихся прямых. Частично с пересекающимися прямыми они знако-

мились при изучении углов, при построении многоугольников и т. д. Учитель рассматривает с учащимися различные случаи пересече­ния прямых на плоскости. При пересечении двух прямых образуют­ся четыре угла с общей вершиной в точке пересечения прямых. Углы будут острые (их два) и тупые (их два) или прямые (все четыре).

Учащиеся учатся определять с помощью чертежного треуголь­ника, какие углы образовались при пересечении двух прямых.

Рассматривается пересечение прямых под прямым углом как наиболее часто встречающееся в жизни. Школьники в классе отыс­кивают на окружающих предметах прямые, которые пересекаются и образуют при этом прямые углы. Например, планки классной доски. Учитель сообщает учащимся, что такие прямые называются перпен­дикулярными. Одна такая прямая по отношению к другой являет­ся перпендикуляром.

Далее учитель знакомит учащихся с построением взаимно пер­пендикулярных прямыхс помощью линейки и чертежного треуголь­ника. Их построение существенно не отличается от построения пря­мого угла. Если стороны прямого угла продолжить за вершину, то образуются взаимно перпендикулярные прямые. Должны быть рас­смотрены следующие случаи построения перпендикулярных прямых:

1) Дана точка, требуется построить две прямые (два отрезка), перпендикулярные друг другу и пересекающиеся в данной точке. Учащиеся проводят через точку произвольную прямую, затем в дан­ной точке строят прямой угол с помощью чертежного треугольни­ка. Продолжая сторону угла, получают взаимно перпендикулярные прямые.

2) Дана прямая, на прямой задана точка, требуется построить прямую, перпендикулярную данной и проходящую через данную точку. По-другому: требуется провести перпендикуляр к данной пря­мой в данной точке. Это задание является частью предыдущего.

3) Даны прямая и точка вне ее, требуется провести через дан­ную точку прямую, перпендикулярную к данной прямой. По-дру­гому: провести перпендикуляр из точки к прямой.

Школьники располагают чертежный треугольник так, чтобы один его катет совпадал с прямой, а вершина — с данной точкой (рис. 5), и проводят по второму катету прямую через данную точку. Она будет перпендикулярна к данной прямой. Учащиеся должны сами в этом

убедиться, прикладывая чертежный треугольник к образующимся при пере­сечении прямых углам (все четыре угла прямые).

Пересекающиеся прямые могут не пересекаться на чертеже, т. е. точка их пересечения располагается где-то за краем листа бумаги, плоскости клас­сной доски. Учитель предлагает школь­никам построить прямую, расположив ее наиболее удобно на листе бумаги. Вторую прямую дети строят выше пер-

вой наклонно к ней, но не пересекают прямые. На первой прямой изображаются 3—4 точки, в которых проводятся пер­пендикуляры до пересечения со второй прямой.

Отрезки перпендикуляров, заключенные между прямыми, измеря­ются, их длины сравниваются между собой. Школьники делают вы­вод, что прямые должны пересечься, но точка пересечения находит­ся за пределами чертежа.

Учитель проводит на доске две горизонтальные прямые и про­сит кого-либо из учеников изобразить несколько точек на одной прямой и через них провести перпендикуляры до пересечения с другой прямой, измерить длины отрезков, заключенных между пря­мыми, и сравнить их. Школьники устанавливают, что длины всех отрезков одинаковы. Поэтому можно сделать вывод: так как расстоя­ние всюду одно и то же, то эти прямые не пересекаются. Они парал­лельны. Учитель говорит: «Если две различные прямые на плоскос­ти не пересекаются (не имеют общих точек), то они называются параллельными».

Далее проводятся упражнения, которые способствуют закрепле­нию образов параллельных и перпендикулярных прямых, их назва­ний, выделяются такие прямые на окружающих предметах.

Учителю вспомогательной школы необходимо помнить о том, что учащиеся слабо дифференцируют параллельные и перпендику­лярные прямые и их положение в пространстве — горизонтальное, вертикальное, наклонное. Нередко дети параллельные прямые называют горизонтальными прямыми, чертят их только в горизонтальном положении, если же параллельные даны в вертикальном или наклонном положении, не узнают их как параллельные. Поэтому в этот период необходимы упражнения на дифференциацию этих понятий, предупреждающие закрепление неверных представлений и понятий у учащихся. Нужно научить детей определять взаимное положение прямых на окружающих их предметах. Следует также широко применять на уроках индивидуальные карточки с изображением пересекающихся и параллельных прямых, например, рейки, палочки, которые учащиеся располагают в различных положениях относительно друг друга: две рейки взаимно перпендикулярны или взаимно параллельны, на­ходятся в горизонтальном (вертикальном, наклонном) положе­нии и т. д.

Школьники не должны ограничиваться узнаванием прямых на глаз. В каждом отдельном случае им следует предлагать измерить расстояние между прямыми и установить, приближаются они друг к Кругу или нет.

Вычерчивание параллельных прямых представляет большую трудность для учащихся.

Рассмотрим один из приемов построения произвольных парал­лельных прямых. Учащимся предлагается положить линейку на лист бумаги наиболее удобным способом (лучше параллельно нижнему (верхнему) краю листа). Чертежный треугольник прикладывается к линейке одной стороной прямого угла и перемещается по линейке.

Рис. 6.

По второй стороне прямого угла чертежного треугольника прово­дятся прямые линии. Эти прямые будут параллельными между со­бой (рис. 6).

Затем линейку можно положить перпендикулярно к нижнему краю листа или наклонно (рис. 6 и рис. 7).

Но, как правило, детям трудно удержать одновременно одной левой рукой и линейку, и чертежный треугольник, поэтому лучше сначала провести по линейке прямую, а затем изобразить на ней на заданном расстоянии точки и провести через них перпендикуляры к прямой (рис. 8).

Задача построить параллельные прямые может быть ограниче­на дополнительным условием. Например, даны отрезок прямой АВ и точка М вне его, требуется провести через точку М прямую, парал­лельную отрезку АВ (рис. 9). В этом случае из точки М проводится перпендикуляр МК к АВ и через точку М проводится прямая

CD ^ MK.

Параллельные и перпендикулярные прямые обязательно стро­ятся в различном положении по отношению к краям листа бумаги
(рис. 10).

КРУГ. ОКРУЖНОСТЬ

В I и II классах учащиеся знакомятся с кругом и шаром. Следует показать учащимся, что если положить кружок (модель круга), ша­рик на какую-либо плоскую (горизонтальную) поверхность, например на стол, то кружок будет лежать, а шарик, скорее всего, покатится. Сопоставление круга и шара поможет их дифференциации.

Дети учатся среди окружающих предметов узнавать те, которые имеют форму круга или шара. Например, донышко чашки, стакана, ведра и т. п. имеют форму круга, а апельсин, мяч, арбуз — форму шара. Полезно проводить игру «Найди похожий». Учащиеся получают модели круга и шара и карточки с изображением предметов, имеющих форму круга и шара. Они должны около круга положить вce карточки с предметами, похожими на круг, а около шара — карточки с изображением предметов, похожих на шар. Выигрывают те ребята, которые не допустили ни одной ошибки.

В процессе обучения математике учащиеся часто пользуются кругами в качестве счетного материала, но не в качестве предмета для изучения. Необходимо сделать круги предметом изучения, сле­дует научить учащихся сопоставлять круги, пользуясь приемом на­ложения. Например, желтый круг меньше красного, так как он по­местился внутри красного круга.

Проводятся практические работы и с моделями и трафаретами круга. Учитель показывает, как обводить круг и раскрашивать часть плоскости внутри полученной кривой линии. Задания для учащих­ся могут формулироваться так: «Возьмите шаблон круга. Обведите круг. Какая у вас получилась линия? Получилась кривая линия. За­штрихуйте (закрасьте) круг. Что заштриховали? Чем? Как?»

Понятие «окружность» при обводке круга вводится только в III классе.

Окружность проводится карандашом одного цвета, а круг за­штриховывается карандашом другого цвета. В классе следует де­монстрировать таблицу, на которой жирной линией вычерчена окруж­ность, а рядом изображен круг (заштрихована часть плоскости).

Далее учащиеся знакомятся с вычерчиванием окружности с по­мощью циркуля (на бумаге), с помощью колышка и нити с привя­занной палочкой (на земле).

Учитель предлагает раздвинуть ножки циркуля и начертить окружность. Не все дети сразу овладевают приемом черчения, неко­торые не смогут повернуть кисть руки так, чтобы концы кривой линии соединились, некоторые не смогут одновременно оказывать давление на обе ножки циркуля, поэтому ножка циркуля вырвется из бумаги, грифель сломается. Нужно давать ученикам тренировочные зада­ния по вычерчиванию окружности на отдельных плотных листах бумаги. Большинству учащихся требуется оказывать индивидуаль­ную помощь: держать головку циркуля вместе с ними.

Как только дети научатся вычерчивать окружность, следует со­средоточить их внимание на двух понятиях — центр и радиус. Уча­щимся надо показать на чертеже, сделанном на доске, на листе бу­маги, след от острия ножки циркуля и сказать, что эта точка назы­вается центром круга и окружности. Если круг вырезан из бумаги, то центр можно найти, дважды перегнув круг пополам. Центр — точка. Учащимся предлагается соединить центр отрезками с несколь­кими точками, принадлежащими окружности. Эти отрезки назы­ваются радиусами круга или окружности. Радиусы можно изме­рить. Измерив радиусы, учащиеся убеждаются в том, что все ра­диусы данной окружности (круга) равны. По заданию учителя уча­щиеся проводят еще несколько радиусов. Этим самым мы подводим детей к выводу о том, что в круге и окружности можно провести сколько угодно радиусов. Учащиеся учатся чертить окружности заданного радиуса.

Сопоставление круга и окружности проводится в ходе практи­ческих работ: раскрашивание карандашами различного цвета окруж­ности и круга; определение на чертеже точек, принадлежащих окруж­ности; принадлежащих кругу, но не принадлежащих окружности; на­ходящихся вне круга и окружности.

Далее учащимся нужно дать понятие о том, что размер круга, длина окружности зависят от длины радиуса. Предлагается начер­тить рядом две окружности разных радиусов и сравнить их «на глаз».

То же следует проделать и с кругами. Затем дается задание вы­резать круги одинаковых и разных радиусов и сравнить их путем наложения. Наконец, предлагается начертить окружности с одним центром (т. е. концентрические окружности), но с разными радиу­сами и сравнить их размеры. Ученики убеждаются, что, чем больше радиус, тем больше длина окружности и тем больше круг.

Для развития ориентировки на плоскости рассматриваются раз­личные случаи взаимного положения прямых и окружностей: пря­мая и окружность не пересекаются и не касаются (не имеют общих точек); прямая находится рядом (около, близко, далеко) с окруж-

ностью; прямая пересекает окружность (имеет с ней две общие точки); прямая касается окружности (имеет с ней одну общую точку); окружности не пересекаются; окружности пересекаются (имеют две общие точки); окружности касаются (имеют одну общую точку). Окружность и дуга сопоставляются между собой. Дуга — часть окружности, поэтому вычерчивается данным радиусом. В IV классе окружность рассматривается как пример кривой замкнутой линии, дуга — кривой незамкнутой линии.

В VI классе учащиеся знакомятся с новой линией в круге — диаметром. Дети могут самостоятельно прийти к выводу, что длина диаметра равна длине двух радиусов и что в круге можно провести много диаметров.

Ученики VI класса вспомогательной школы должны понимать, что радиус и диаметр — это отрезки: радиус — это отрезок, который соединяет центр круга (окружности) и точку, принадлежащую окружности, диаметр — это отрезок, который соединяет две точки, принадлежащие окружности, и проходит через центр круга. Учащимся могут быть даны задания: вычислить радиус круга по данной длине диаметра; вычислить диаметр круга по длине радиуса. На уро­ках геометрии необходимо чередовать задания: вычертить окруж­ность по данному радиусу, вычертить окружность по данному диа­метру. Выполнив чертеж, дети сравнивают свои работы, для того чтобы убедиться в том, что получены одинаковые окружности. Затем учащиеся знакомятся с еще одной линией в круге — хордой, являющейся отрезком, который соединяет две точки окружности. В одном и том же круге хорды могут быть разной длины, Школьники получают задание вычертить сначала произвольную хорду, а затем хорду большей или меньшей длины. Наблюдая измерение длин хорд вследствие изменения их положения относительно центра, они должны самостоятельно сделать вывод о том, что та хорда имеет большую длину, которая ближе к центру (и наоборот). Обычно с интересом дети размышляют над такими вопросами: если имеется круг радиусом 5 см, то может ли быть в нем проведена хорда длиной 20 см, 6 см, 11 см? В ходе такой работы устанавливается, что длина любой хорды не может быть более длины диаметра. Ученикам разъясняется, что диаметр — самая большая хорда.

Для дифференциации радиуса, диаметра, отличной от диаметра хорды можно проводить не только упражнения по их вычерчива­нию в круге, но и диктанты. Учащимся предлагается начертить круг, провести в нем линии (радиус, диаметр, любую другую хорду), затем под диктовку учителя изобразить точки, принадлежащие окружнос­ти, не принадлежащие окружности, но принадлежащие кругу; при­надлежащие диаметру, радиусу, произвольной хорде.

Учащиеся уже знают приемы сравнения кругов наложением, по длине радиусов. Теперь следует учить их сравнивать круги по длине диаметров. Получив задание вычертить круги с одним центром, но разными диаметрами, дети убеждаются в том, что, чем больше (мень­ше) длина диаметра, тем больше (меньше) длина окружности, раз­мер круга.

Все те знания, умения и навыки, которые приобретают учащиеся в VI классе, закрепляются на следующих годах обучения.

Длина окружности

В VIII классе наиболее хорошо успевающих учащихся можно познакомить с длиной окружности и способом вычисления длины окружности (или даже формулой). Этот материал можно вынести на внеклассную работу по математике.

Ознакомление с длиной окружности целесообразно начать с соз­дания такой ситуации, чтобы дети почувствовали необходимость вычисления длины окружности. Например, требуется окантовать несколько кругов лентой. Учащиеся поставлены перед решением задачи: хватит ли для всех кругов имеющейся ленты. Учитель спра­шивает, как решить такую задачу. Опыт показывает, что в подобной ситуации школьники пытаются выложить ленту по окружности круга. Иногда они предлагают взять нитку, опоясать ею окружность и затем измерить длину нитки. Учащиеся убеждаются в трудности этих опе­раций.

Затем учитель дает задание измерить длину окружности, начер­ченной на доске, на бумаге, учащиеся убеждаются, что в этом случае предложенный ими способ измерения окружности непригоден. Опыт показывает, что лучше не давать учащимся готовую формулу вычис­ления длины окружности, а привлечь их к выводу формулы. С этой целью можно использовать разные способы. Например, каждому ученику предлагается взять заранее изготовленный круг из тонкой бумаги (с длиной диаметра, выраженной целым числом), разделить его перегибанием пополам, т. е. получить диаметр круга. Взять нитку и, выпрямив ее, приложить к диаметру, отрезать кусок нитки, равный по длине диаметру. На окружности выбрать точку, в которой закре­пить конец заготовленного куска нитки. Нитку накладывать на ок­ружность, отмечая точкой положение, в котором окажется другой конец нитки. Учащиеся убеждаются, что диаметр укладывается по окружности чуть больше трех раз. Если диаметр был 8 см, то длина окружности будет чуть больше 24 см. Учитель сообщает детям: «Уче­ные установили, что длина любой окружности приблизительно в 3,14 раза больше длины ее диаметра». Значит, чтобы вычислить длину окружности, нужно измерить ее диаметр и получившееся число ум­ножить на 3,14. Если длину окружности обозначить буквой С, длину диаметра — буквой D, то получим C » 3,14*D) (число 3,14, выражаю­щее отношение длины окружности к длине ее диаметра, для всех окружностей одно и то же и обозначается греческой буквой p), C = pD, C = p-2R, или C = 2pR.

Можно вывести формулы длины окружности другим способом: учитель предлагает учащимся изготовить модели кругов данных диа­метров, измерить с помощью нитки длину их окружности и резуль­таты внести в таблицу. Затем определить, измерив длину диаметра, во сколько раз длина окружности больше длины ее диаметра (вычис­ления производятся с точностью до 0,01).

Результаты у каждого ученика будут близки к 3,14. Делается вывод, что длина окружности больше длины диаметра в 3,14 раза. А если известна длина диаметра (или радиуса), то можно вычис­лить и длину окружности.

Чтобы учащиеся убедились, что результат при вычислении длины окружности по формуле совпадает с результатом при измерении (близок к нему), можно предложить сначала измерить длину окруж­ности какого-либо круга, а затем вычислить ее по формуле и сравнить полученные числа. Для запоминания формулы решаются задачи.

Сектор, сегмент

В IX классе к тем знаниям, которыми уже овладели учащиеся, добавляются сведения о частях круга — секторе и сегменте. При изучении обыкновенных дробей школьники делили круг на равные части, поэтому, как разделить круг пополам, на четыре доли, восемь, шестнадцать долей, три, пять, они уже знают.

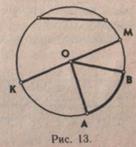
В IX классе школьникам вновь предлагается разделить круг на 3—4 равные части, обращая их внимание на то, что каждая часть, ограниченная двумя радиусами и дугой окружности,— это сектор.В круге можно выделить много секторов, как равных между собой, так и неравных. Дети вычерчивают круг и несколько его секторов. Сектор обозначается тремя буквами. Например, на рисунке 11 изо­бражен сектор АО В.

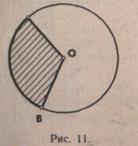
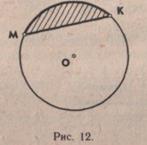
Ученикам предлагается провести хорду и закрасить (или заштри­ховать) разным цветом полученные части круга. Учитель сообщает, что часть круга, которая находится между хордой и дугой окружнос­ти, называется сегментом(рис. 12). Учащиеся проводят в круге 2—3 хорды, называют и показывают полученные сегменты. Им полезно рассмотреть чертежи, где изображены разные линии в круге, назвать их, назвать и показать образованные в круге сегменты, секторы (рис. 13).

Диаграммы

К концу обучения во вспомогательной школе (IX класс) уча­щиеся должны научиться читать, понимать и вычерчивать линейные, столбчатые и круговые диаграммы. В газетах, журналах, научных изданиях встречаются различные диаграммы. Они наглядно по­казывают соотношение отдельных количественных показателей, повышение или понижение выпуска промышленных изделий, сельско­хозяйственной продукции, изменения цен и т. д. Диаграммы позво­ляют легко установить динамику происходящих изменений (расшире­ние или уменьшение производства, затрат труда, изменение произ­водительности труда и т. д.).

Наиболее легкими для чтения и понимания являются линейные и столбчатые диаграммы.

Рассмотрим построение линейной диаграммы.

3 а д а ч а. В классе 16 человек, — часть из них девочки, а осталь­ные мальчики. Сколько мальчиков в классе?

Решение.

1) Сколько девочек в классе?

¼ от 16 чел. 16 чел.:4 = 4 чел.

2) Сколько мальчиков в классе?
16 чел.—4 чел. = 12 чел.

Ответ. В классе 12 мальчиков.

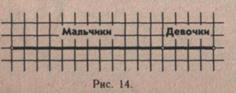
Построим линейную диаграмму состава учащихся класса.

Выберем условную единицу изображения одного ученика — длину клеточки.

Следовательно, всех учеников класса

условно можно изобразить отрезком дли­ной в 16 клеточек.

Мальчики — отрезок длиной в 12 кле­точек.

Девочки — отрезок длиной в 4 кле­точки.

Линейная диаграмма состава учащих­ся класса (рис. 14).

Строим диаграмму. Отрезки можно располагать горизонтально или верти­кально.

Обычно под диаграммой помещается

текст, который диаграмма иллюстрирует, делает наглядным те коли­чественные показатели, которые отражены в тексте. Чтобы учащиеся поняли диаграмму и научились ее читать, необходимо вместе с ни­ми прочитать текст, выделить в нем числовые данные и показать, как они воплощены в диаграмме.

Рассмотрим столбчатую диаграмму,над ней написано: «Диаграм­ма состава учащихся 5-го класса» (рис. 15).

Учитель показывает и рассказывает учащимся содержание и по­строение этой диаграммы. Он говорит, что в V классе 15 учеников. Это количество на столбчатой диаграмме обозначено столбиком. В столбике содержится 15 клеток (высота). Это значит, что каждый ученик условно обозначен на диаграмме клеточкой. Рядом построен столбик, обозначающий количество мальчиков. Их 10 человек, так как этот столбик имеет высоту в 10 клеток, а третий столбик озна­чает число девочек. Их 5, так как 3-й столбик имеет высоту в 5 кле­точек.

Следовательно, чтобы понимать и прочитать диаграмму, нужно не только знать, о чем идет речь в диаграмме, т. е. какие количествен­ные показатели она отражает, но и выявить условную меру для по­строения диаграммы.

Столбчатые диаграммы можно читать и вычерчивать даже в млад­ших классах. Так, вычерчиваются диаграммы, соответствующие чис­лу мальчиков и девочек в классе, количеству серых и белых кроли­ков в кружке и т. п. Для детей такие диаграммы не представляют трудности, так как одной клеткой или группой клеток изображается единичный предмет.

Особые трудности возникают у учащихся тогда, когда требуется выбрать ту меру, которая будет изображаться одной клеткой, одним прямоугольником и т. п. Например, с участка собрано 500 кг моркови и 650 кг свеклы. Что принять за меру? Учитель должен подсказать, что следует изображать одной графической единицей (например, клеткой в тетради по математике) 50 кг собранных овощей.

Наиболее трудными для вычерчивания являются круговые диа­граммы.Только после знакомства учащихся с сектором можно при­ступать к изготовлению круговых диаграмм. К трудностям, связан­ным с выбором меры, добавляется еще одна — деление круга на секторы в соответствии с тем, сколько раз единичная мера содер­жится в данных условиях задачи. Школьники IX класса умеют делить круг на 2, 4, 8, 16, 32, 64, ... равные части, а также на 3, 6, 12, 24, 48, ... равных частей. Можно научить их делить на 5, 10, 20, 40, ... равных частей.

Учитель объясняет, что, кроме линейных и столбчатых диаграмм, можно строить и круговые диаграммы. Круговая диаграмма по­лучила название от слова «круг». Круг принимают за единицу и делят его на доли — секторы.

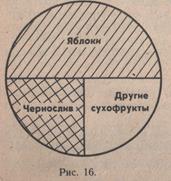
Ознакомление с круговой диаграммой проводится на простом примере. Например, нужно в виде круговой диаграммы изобразить

состав сухофруктов в 1 кг компота, если в нем содержится — кг яблок,

— кг чернослива, — кг других сухофруктов. За 1 кг компота при­нимаем круг. Разделим его на 4 равные части. Надо найти и обозна­чить — часть круга — яблоки, — часть круга — чернослив, — часть

круга — другие сухофрукты (рис. 16).

Решим более трудную задачу. «Всего на делянке 1200 деревьев. Из них 800 деревьев составляют липы, а остальные деревья — дубы. Изобразить в виде круговой диаграммы сорта деревьев». Все деревья (1200) изображаем кругом. Круг надо разделить на 12 равных сек­торов, каждый из которых будет соответствовать 100 деревьям, или на 6 равных секторов, каждый из которых будет изображать 200 де­ревьев. Мера должна быть достаточно крупной, содержаться в дан­ном числе (1200) целое число раз. Закончить решение задачи. Если бы задача с деревьями была бы сформулирована так: «В парке было 800 лип и 400 дубов» — и требовалось бы вычертить круговую диа­грамму, то сначала следовало бы вычислить сумму тех и других де­ревьев, а затем выбирать меру.

Круговые диаграммы школьники должны уметь читать, вычерчи­вать как можно чаще, необязательно на уроках геометрии. На уроке математики при работе над арифметической задачей в качестве ил­люстрации к ней может быть начерчена диаграмма. Например: «1/5 поля была засеяна гречихой, 2/5 — просом, остальная земля была за­сеяна горохом. Какая часть земли засеяна горохом?» Рассмотрев
дроби, учащиеся могут сказать, что все поле следует принять за единицу. Обозначим все поле целым кругом. Так как знаменатели дан­ных дробей — 5, то поле разделено на 5 долей, т. е. круг надо делить на 5 равных секторов. Один сектор закрасим одним цветом, два дру­гих — другим. Оставшиеся два сектора — третьим. Они будут изоб­ражать тот участок земли, который занят горохом (рис. 17).

Построение линейного графиканачинается с вычерчивания пря­мого угла, стороны которого являются частью осей координат, а

вершина — нулевой точкой отсчета. Затем следует выбор тех мер, которые откладываются от нуля по осям. Например, учащиеся класса выполняют производственные заказы, ежедневно подсчитывается выработка, а может быть, выручка за изготовленную продукцию. По начерченной оси абсцисс через равные промежутки отмечаются точки, соответствующие рабочим неделям, по начерченной оси ординаты - полученная продукция (каждое деление на оси — продукция в штуках, в десятках штук или сотнях). Отмечая точки на пересе­чении линий, параллельных осям, затем соединяя их, учащиеся получают непрерывную линию—график, который четко показывает подъем или падение выработки.

УГЛЫ

Во II классе учитель впервые знакомит учащихся с понятием угол. Сначала он просит детей назвать и показать углы, т. е. выявляет знания об углах, затем раздает ученикам листы бумаги неопределенной (не прямоугольной) формы, такой же лист оставляет себе.

Под руководством учителя дети перегибают лист один раз, потом второй. Развернув лист, они находят точку пересечения линий сгиба, отмечают ее карандашом, а затем от нее по линейке проводят по линиям сгиба два луча. Учитель говорит детям, что они получили угол, и просит присмотреться повнимательнее, один ли получился угол, т. е. нельзя ли провести еще лучи по линиям сгиба из той же точки. Дети находят, что углов четыре.

При сложении вчетверо листа бумаги по линиям сгиба углы накладываются друг на друга, значит, углы между собой равны. Школьники снова разворачивают лист, рассматривают каждый из полученных углов. Учитель говорит, что это прямые углы. Далее он знакомит учащихся с элементами угла — вершиной и сторонами угла. Вершина — это точка (показывает), откуда выходят два луча — стороны. Учитель задает вопросы: «Как получили прямой угол? Перегните два раза лист бумаги, так, чтобы получился угол. Где вершина угла? Чем является вершина угла? Как еще можно назвать стороны угла?»

Далее учащиеся знакомятся с чертежным треугольником. На чертежном треугольнике они отыскивают прямой угол, находят его вершину, стороны. Познакомившись с прямым углом чертежного треугольника, дети должны научиться им пользоваться как для вычерчивания прямого угла, так и для определения вида углов, которые встречаются им на чертежах или предметах. Чтобы вычертить прямой угол с помощью чертежного треугольника, ученики должны положить чертежный треугольник на лист бумаги, отметить точку — вершину угла, точку на одной стороне угла и точку на другой стороне угла чертежного треугольника. Убрав чертежный треугольник, дети чертят прямой угол, проводя лучи из вершины угла через каждую из двух отмеченных точек.

Чтобы не ошибиться и правильно провести стороны угла, т. е.

лучи, необходимо отметить вершину более четкой (заметной) точкой.

Научившись вычерчивать прямой угол, школьники быстрее уз­нают его на предметах, среди других углов, на моделях и чертежах геометрических фигур. Учитель изготавливает таблицу, на которой среди острых и тупых углов будут находиться и прямые углы (в привычном положении, когда одна из сторон параллельна краю листа), и дети должны только узнать прямые углы. Предъявив чертежи квадрата или любого другого прямоугольника, учитель закрывает ту часть фигуры, где расположены три ее вершины. Дети должны узнать в оставшейся части прямой угол. Узнав таким образом каждый угол прямоугольника (квадрата), учащиеся говорят, что у любого прямоугольника все углы прямые.

Когда для детей не будет представлять трудности узнавание прямого угла в одном и том же положении, следует перейти к вычерчиванию прямого угла в других положениях (по отношению к краям листа бумаги). Узнать прямой угол в таком положении на глаз трудно, поэтому необходимо овладеть приемом определения вида угла с помощью чертежного треугольника. Учащиеся должны не только научиться правильно накладывать чертежный треугольник на чертеж, но и рассказывать, как они это делают: «Треугольник надо положить не чертеж так, чтобы вершина его прямого угла совпадала с вершиной данного угла и чтобы сторона прямого угла! треугольника совпала со стороной данного угла. Если при этом вторая сторона прямого угла чертежного треугольника совпадает со второй стороной данного угла, то этот угол прямой».

Если некоторые школьники будут испытывать затруднения при составлении такого подробного отчета, можно сделать его короче. Так, слова «вершина данного угла» или «вершина чертежного треугольника» и ряд других можно заменить показом. Ученик указы­вает вершины и говорит: «Эта вершина должна совпасть с этой, эта сторона — с этой...»

Далее учитель дает задание показать прямые углы на окру­жающих предметах, чертежах, орнаментах и т. д.

Сначала учащиеся определяют вид угла на глаз и только после этого определяют вид угла с помощью чертежного треугольника.

Затем учитель знакомит учащихся с острыми и тупыми углами, сравнивая их с прямым углом, ученики определяют вид этих углов также с помощью чертежного треугольника. Работа ведется с чер­тежным треугольником из прозрачного материала, чтобы при нало­жении его на данный угол можно было видеть расположение сторон угла.

При наложении углов возникают такие ошибки: школьники сов­мещают одну сторону угла чертежного треугольника со стороной данного угла, но не совмещают вершины углов; совмещают вершины сравниваемых углов, но не совмещают соответствующие стороны. Сравнение углов некоторым учащимся нередко легче проводить не на моделях, а на чертежах, так как ярче виден результат наложения прозрачного чертежного треугольника на данный угол.

Учитель подводит школьников к выводу о том, что все прямые

углы равны, а острые и тупые углы могут быть разной величины. Учащиеся учатся сравнивать, используя прием наложения, острые, тупые углы и устанавливать, какой угол больше, какой